ЛАБА 2
.docxМІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
НАЦІОНАЛЬНИЙ АВІАЦІЙНИЙ УНІВЕРСИТЕТ
ФАКУЛЬТЕТ ТРАНСПОРТНИХ ТЕХНОЛОГІЙ
Лабораторна робота №2
з дисципліни
«Теорія ймовірностей та математична статистика»
Варіант-14
Виконала
студентка групи ОП-202
Саламаха Єлизавета Романівна
викладач Горідько Р.В.
Київ 2018
Повторні незалежні випробування (схема Бернуллі)
Мета та основні завдання роботи: за допомогою пакету Microsoft Excel навчитися розв’язувати задачі, пов’язані з повторними незалежними випробуваннями та основними граничними теоремами схеми Бернуллі
Завдання 1. Знайти ймовірність того, що з 4 отриманих кредитів будуть повернуті:
а) 2 кредитів;
б) не менше 2 кредитів;
в) не більше 2 кредитів;
г) принаймні один кредит.
Імовірність повернення кредиту дорівнює 0,5.
Розв’язання. n=4, p=0,5, q=0,5
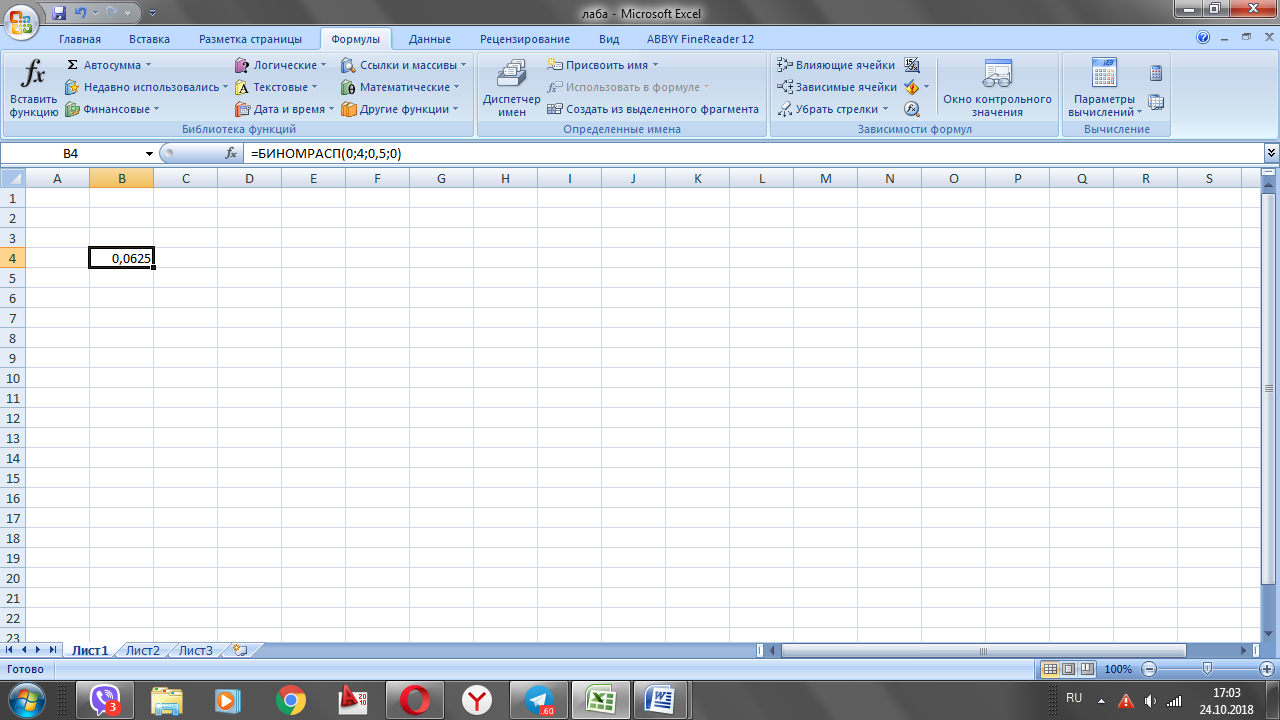
За
формулою:
k=2
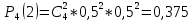
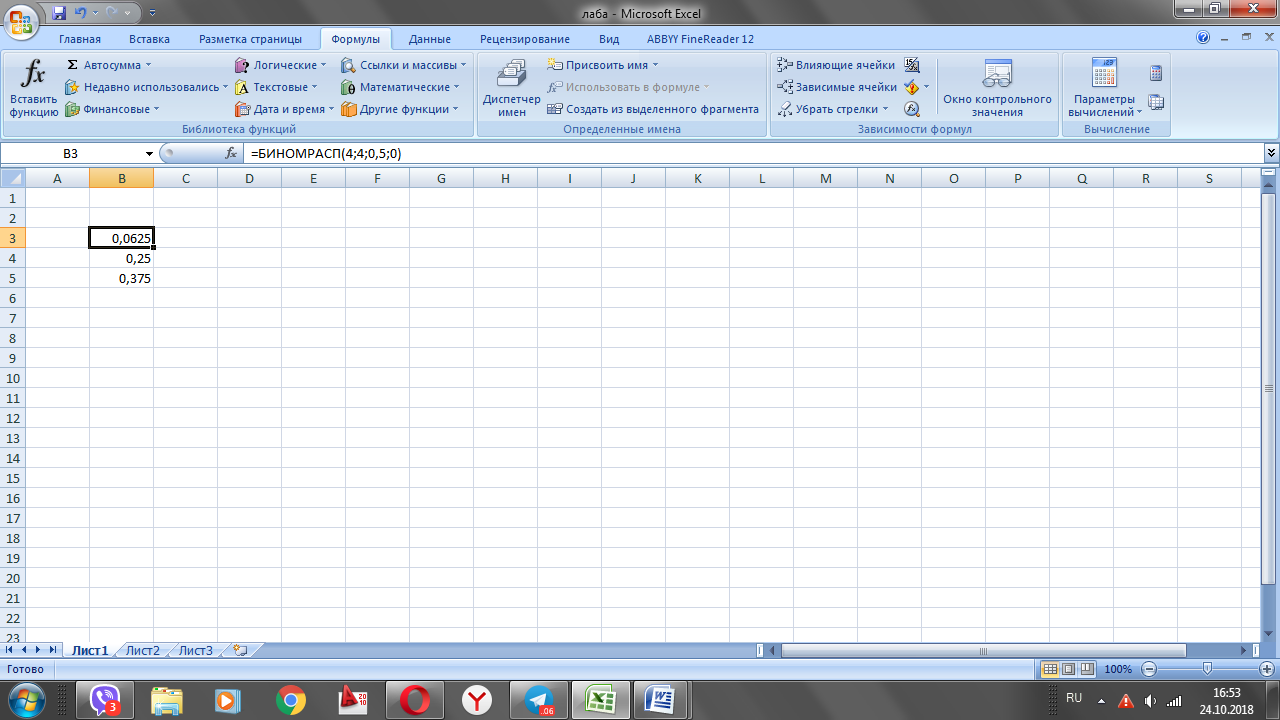
б) k=2;3;4
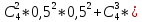
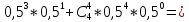0,375+0,25+0,0625=0,688
в) k=0;1;2
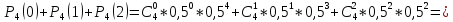0,0625+0,25+0,375=0,688
г) k=1;2;3;4
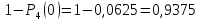
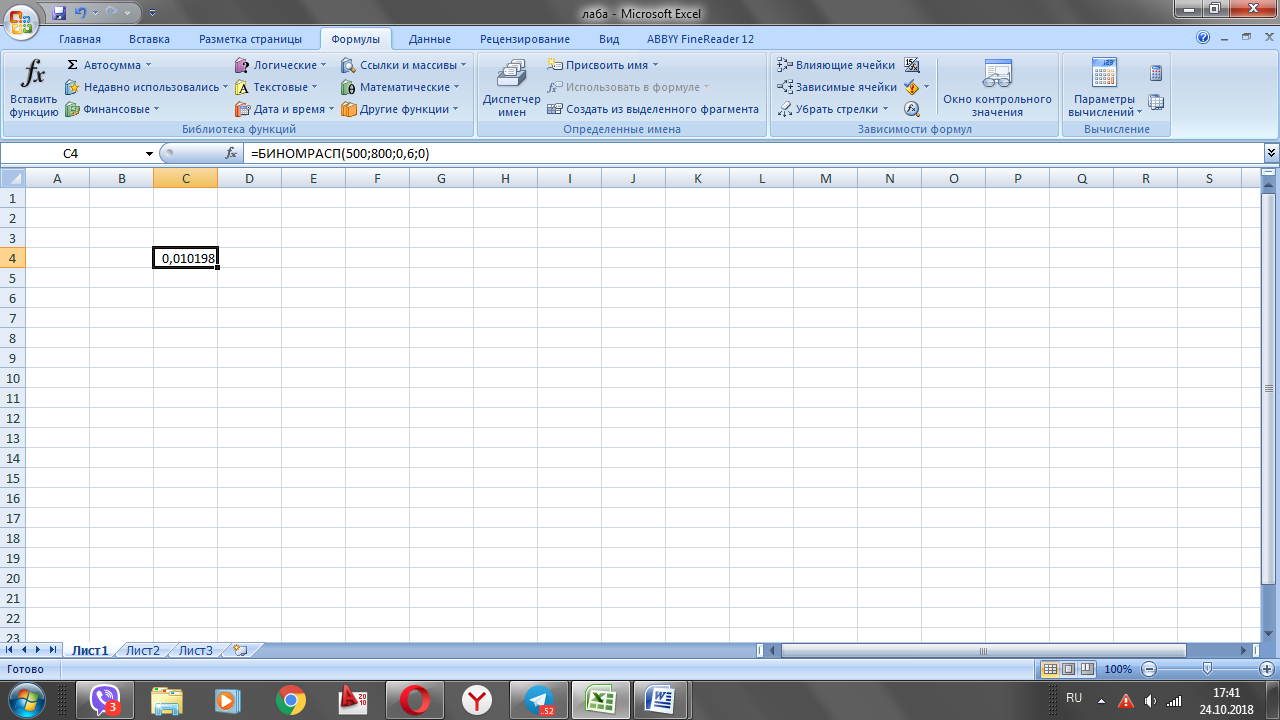
Завдання 2. Знайти ймовірність того, що з 800 посіяних зерен проросте саме 500. Імовірність того, що злак проросте дорівнює 0,6.
Розв’язання. а) n=800, p=0,6, q=1-0,6=0,4, k=500
За
формулою (2.3)
,
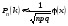де
,
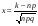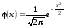локальної теореми Муавра–Лапласа
знайдемо:
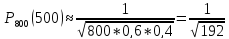φ(1,45)=0,07*0,1394
0,01
Завдання 3. Знайти ймовірність того, що з 120 малих підприємств регіону призупинять свою діяльність від 60 до 70 підприємств. Імовірність того, що мале підприємство збанкрутує за час t дорівнює 0,5.
Розв’язання.
За формулою
(2.4)
,
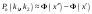де
інтегральної теореми Муавра–Лапласа
знайдемо:
n=120, k1=60, k2=70, p=0,5, q=0,5
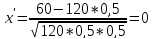
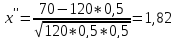
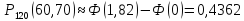
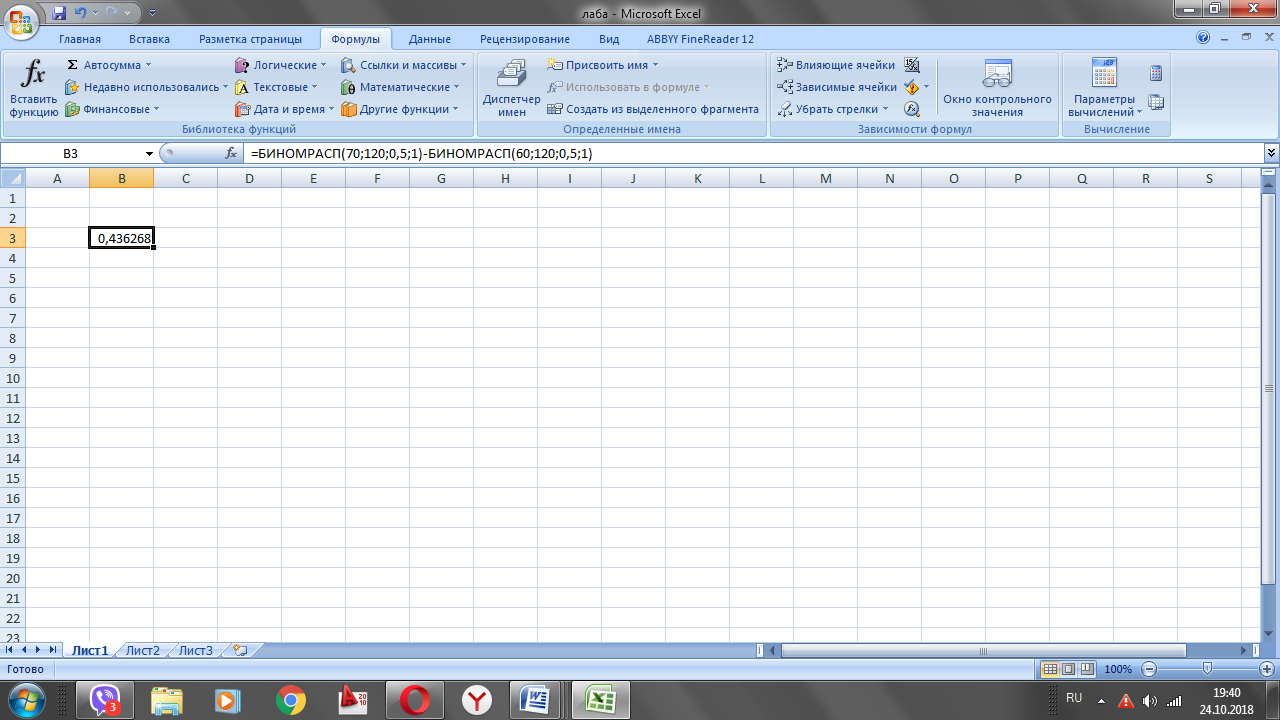
Завдання 4
5. Партія товару, що складається з 1000 виробів, містить 1000 бракованих деталей. Знайти ймовірність того, що навмання узятий виріб містить одну браковану деталь. Передбачається, що число бракованих деталей розподілене за законом Пуассона.
n=1000, p=0,001, k=1
Розв’язання
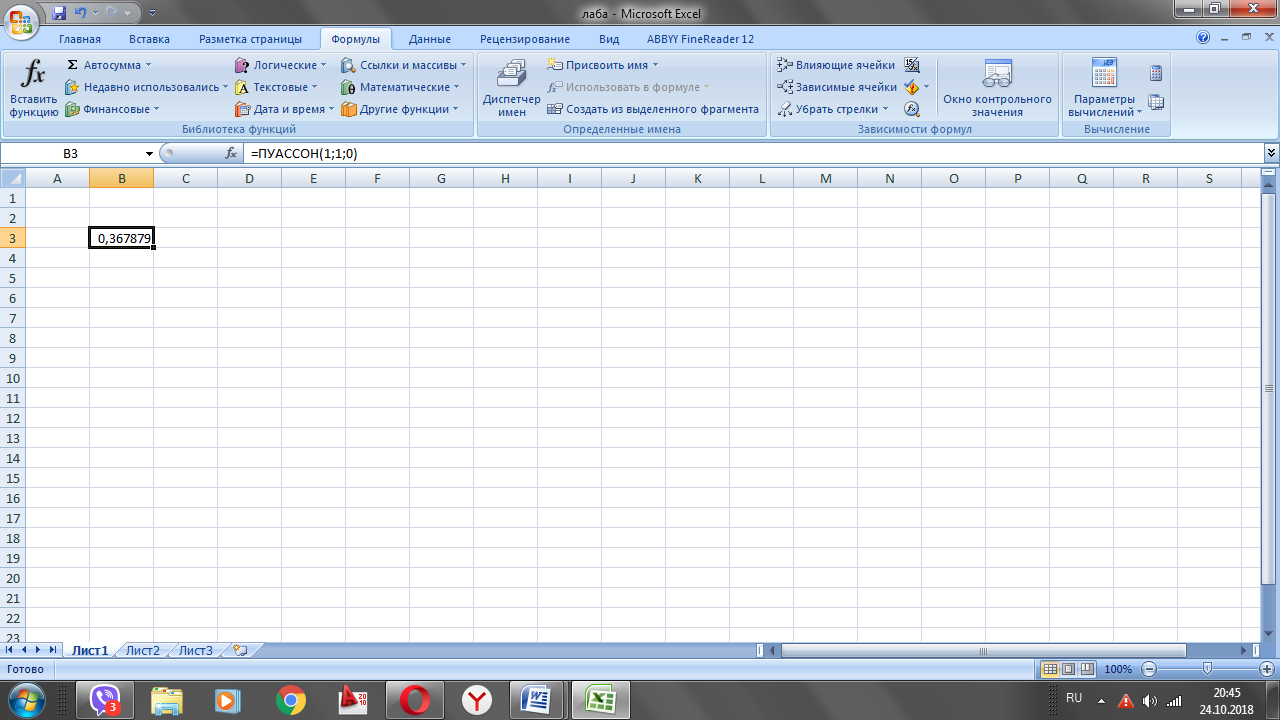
. Застосуємо
формулу теореми Пуассона
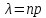
8
Висновок: під час лабораторної роботи я, за допомогою пакету Microsoft Excel навчилася розв’язувати задачі, пов’язані з повторними незалежними випробуваннями та основними граничними теоремами схеми Бернуллі.