Лабораторная работа № 8

«Поиск оптимальных решений в условиях неопределенности целевой функции с планированием эксперимента» (6-8 ч.)

Теоретическое введение

Процедура поиска экстремума при неизвестной целевой функции осуществляется в пошаговом режиме по следующей схеме (Рис.8.1):

1. Выбор начальной точки , проведения эксперимента в ее окрестностях и определение направления градиента. При этом можно использовать полный или дробный факторный эксперименты (ПФЭ и ДФЭ) с шагом варьирования x_i по каждому фактору с определением линейной множественной регрессии

,

где

относительные переменные в стандартизированном масштабе.

Эффекты взаимодействия в данном случае не учитываются для сокращения объема вычислений, т.к. нужно определить не саму поверхность, а лишь направление ее максимального изменения.

2. Осуществление одного шага движения в найденном направлении с определением координат новой точки

где h - выбранный шаг перемещения по градиенту;

- направляющий косинус.

В случае линейной формы регрессии целевой функции частные производные по координатам и направляющие косинусы определяются как

,

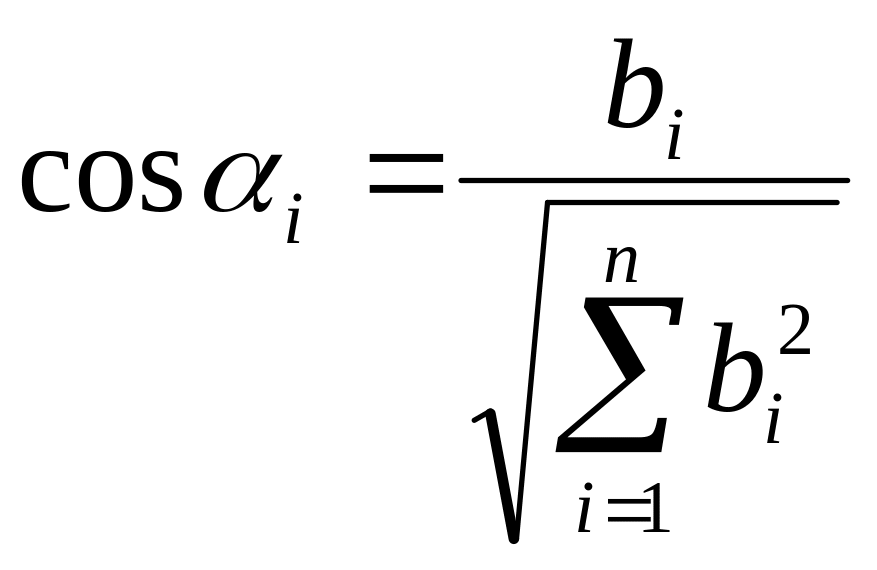что существенно упрощает вычисление градиента и координат новой точки.

Подобная процедура повторяется до тех пор пока все частные производные, т.е. коэффициенты b , не окажутся равным или близкими нулю, что является признаком достижения окрестности точки экстремума.

Рис. 2.32. Поиск экстремума градиентными методами

С использованием факторного эксперимента

Количество опытов резко сокращается при использовании метода крутого восхождения, при котором перемещение в найденном направление от исходной точки продолжается до нахождения локального экстремума. При этом на начальном этапе определяется простейшая линейная модель приближенного описания области далекой от оптимума, после чего осуществляется поиск области экстремума и далее на заключительном этапе строится нелинейная модель в виде полинома 2-го порядка, описывающего функцию отклика вблизи экстремума.

Так как регрессионные модели используются лишь для выбора нужного направления, то в оценке их адекватности возможны определенные компромиссы . Если какой-то из коэффициентов b_i оказывается незначимым, движение по градиенту можно продолжить, изменяя соответствующий фактор x_i с шагом 2-3 раза большим, чем ранее. Так следует поступать и в случае когда все коэффициенты оказываются незначимыми.

Если модель в целом оказывается неадекватной, движение продолжается для накопления новой информации с изменением либо величины шага, либо числа повторений опытов, либо вида модели.

В общем случае неадекватного описания целевой функции и при невозможности повторов эксперимента после определения координат x_i следует измерить Y(x₁..x_n) и ввести ее значение для дальнейшего определения локального экстремума по методу крутого восхождения.

Задание

По заданному описанию целевой функции f смоделировать процесс нахождения экстремума с использованием пошаговой процедуры ПФЭ и выбором направления восхождения / спуска методами градиента и крутого восхождения.

Порядок выполнения

1. Методом сканирования составить массив значений функции f в координатах Х₁ и Х₂ и построить линии равного уровня.

2. Выбрать исходную точку Х₁ по плану ПФЭ. Найти коэффициент b[i] линейной регрессии: _n

Y = b₀ +  b[i] z [i]

ⁱ⁼¹

3. Рассчитать градиент G и координаты новой точки:

= x_i^k-1 + h cos (a_i) ; i = 1,n.

4. Отметить на графике f направление поиска.

5. Выдать на печать координаты каждого шага перемещения и проверить правильность движения по графику f (Х₁,Х₂).

6. Процесс повторить до приближения к области экстремума. После этого провести эксперимент по ЦКП; найти экстремальное значение целевой функции.

7. Повторить поиск по методу крутого восхождения.

8. На графике поверхности построить симплексную траекторию достижения экстремума.

9. Составить программу модуля симплексного движения на каждом шаге и сопоставить расчетные результаты с графическими.

10. Повторить процедуру «слепого поиска» с использованием симплекс-плана и сопоставить результаты.

11. Составить блок-схему и программу алгоритма поиска, Сопоставить результат с графическими и результатами по предшествующим методам.

Примечание:

Программа поиска должна быть построена из автономных процедурных модулей:

PFE – полный факторный эксперимент, включающий составление

матрицы плана и вычисления коэффициентов регрессии с

проверкой адекватности;

GRAD - вычисление градиента и координат новой точки в пространстве

Х₁…Х_n;

ZKP – центральный композиционный план с формированием матрицы

ЦКП, расчетом коэффициентов квадратичной регрессии и

проверкой гипотез.

VOSHOD – процедура крутого восхождения.

Литература

1. Конспект лекций по курсу «Теория принятия решений»

2. Ю. И. Дягтерев «Системный анализ и исследование операций». М. Высшая школа 1996. –335 с.

3. В. Ф. Капустин «Практические занятия по курсу математического программирования». Издание Ленинградского университета. Л-д. 1976. –191с.

4. Иванов А.З., Круг Г.К., Филаретов Г.Ф. Специальные вопросы планирования эксперимента. Учебное пособие. М. МЭИ, 1980 г., 89 с.

5. Ю. А. Ивашкин «Вычислительная техника в инженерных расчетах». М. Агропромиздат. 1989. –335с.

6. А. Л. Конин, Н. В. Копченова «Методические указания к практическим занятиям по курсу «Математические методы оптимизации». М. МЭИ,1986. –28с.

Требования к отчету

Отчет должен быть отпечатан в версии Word 7.0 и содержать:

1. Постановку задачи и рабочее задание;

2. Численный метод или математическую модель решения задачи;

3. Блок-схему алгоритма;

4. Программу и результаты решения;

5. Графики и анализ результата.