Лабораторная работа № 5 Целочисленное программирование (4 часа)

Теоретическое введение

Общая постановка задачи связана с нахождением значений переменных x_i , при которых достигается экстремум целевой функции

при ограничениях:

; ;

; ;

; -целое число

Целочисленная задача возникает в случае, если по своему смыслу переменные x_j являются существенно целыми, если производится продукция определенными партиями или производится выбор (распределение) объекта по его порядковому номеру.

Дополнительное ограничение на целочисленность, как видно из рис.5.1, сужает область допустимых решений ОЗЛП до точек с целочисленными координатами, изменяя соответственно значение целевой функции.

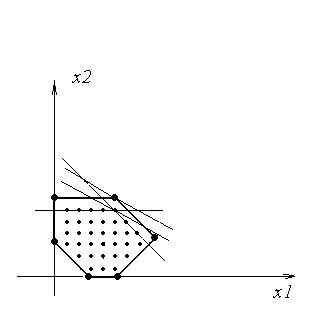Рис. 5.1. Графическая интерпретация целочисленного решения

Методы решения в случае больших по модулю Х основаны на округление результатов до целого и в общем случае на использовании оптимального действительного решения (метод Гомори, метод ветвей и границ).

Алгоритм решения задачи целочисленного программирования по методу Гомори сводится к следующему:

1. Отыскивается оптимальное действительное решение, т.е. решается общая задача линейного программирования.

2. Если все 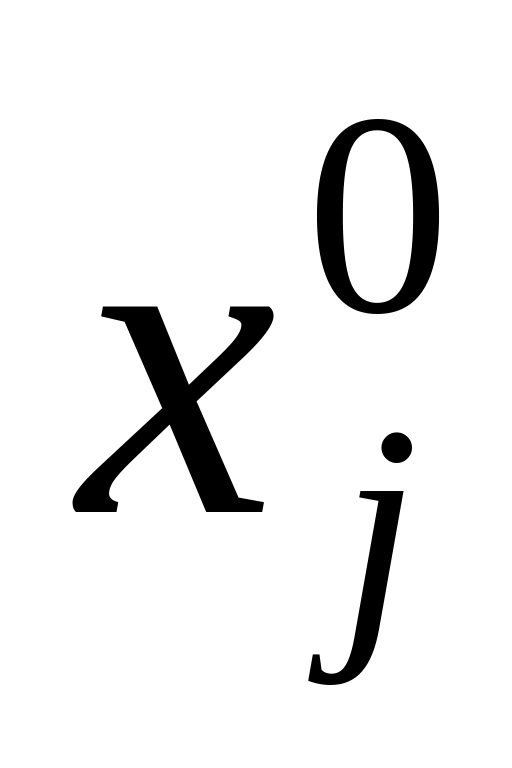- целые числа, то задача ЦП решена.

3. Если нецелые числа, отыскивается число с максимальной дробной частью и составляется дополнительное ограничение по следующим правилам.

Задание и порядок выполнения

Исходя из решения задачи линейного программирования предшествующей лабораторной работы, составить симплексную таблицу с дополнительным условием на целочисленность. При получении целочисленного решения, изменить коэффициенты начальной канонической формы (по своему усмотрению).

Для составленной таблицы:

1. Найти ключевую строку, которая соответствует максимальной дробной части решения и вычислить коэффициенты дополнительной строки для новой дополнительной переменной; составить новую матрицу путем включения в неё столбца и строки для дополнительной переменной;

2. По процедуре нахождения исходного базиса пересчитать составленную матрицу коэффициентов для нахождения целочисленного решения;

3. На области допустимых решений построить дополнительную границу и сопоставить графическое решение с расчетным.

Лабораторная работа № 6

«Решение транспортной задачи» (4 часа)

Теоретическое введение

Сущность классической транспортной задачи состоит в нахождении наиболее выгодного плана-графика перевозок однородного продукта из пунктов отправления к пунктам потребления.

Пусть имеется (см. таблицу) n поставщиков A₁...A_n готовой продукции с объемами продукта и m потребителей B₁...B_m с объемом потребления .

Таблица

Потребит- ли Постав- щики	B1	B2	...	Bm	Объемы поставляемого продукта
A1	x11 C11	x12 C12	...	x1m C1m
A2	x21 C21	x22 C22	...	x2m C2m
...	...	...	...	...	...
An	xn1 Cn1	xn2 Cn2	...	xnm Cnm
Общий объем заказа			...

Необходимо так распределить поставщиков по потребителям, чтобы расходы по доставке продукции или сырья были минимальны, т. е.

,

где

c_ij – транспортные расходы по доставке единицы

продукции от j-го поставщика к i-му потребителю;

x_ij – количество продукта, переводимого из i-го пункта в j-ый.

При этом условие полного удовлетворения потребности в продукте всех пунктов потребления записывается системой уравнений

; ,

а условие полной реализации готового продукта по потребителям уравнением:

; .

Обратные перевозки от потребителя к поставщикам исключаются, т.е.

; ; .

Решение задачи достигается специальными методами линейного программирования, различающимися по принципам расчета оптимальной программы, кругу решаемых задач и эффективности вычислений.

Общий принцип заключается в поэтапном, последовательном переходе от исходного допустимого варианта к оптимальному путем последовательного улучшения предшествующего варианта (распределительный метод, метод потенциалов).

Идея наиболее распространенного метода потенциалов заключается в том, что первоначально определенное тем или иным способом базисное распределение поставок (опорный план) оценивается на оптимальность введением потенциалов строк и столбцов так, что для отличных от нуля элементов опорного плана можно записать уравнение потенциалов

,

из которого следует:

Тогда составляя уравнения потенциалов для конкретных числовых значений , соответствующих ненулевым элементам опорного плана, получаем в результате их решения значения потенциалов и . В случае неопределенности, когда число уравнений меньше числа неизвестных, потенциал первой строки принимается условно равным нулю или какому-либо другому значению.

Зная величины потенциалов и , можно вычислить характеристики псевдозатрат для нулевых переменных опорного плана

.

Тогда, если псевдозатраты не превышают фактические, т.е.

для всех нулевых переменных, то опорный план является оптимальным.

Если данное условие не выполняется, то делается перераспределение поставок. Для этого на матрице плана поставок, исходя из элемента с наибольшим абсолютным значением отрицательной разности , определяется замкнутый контур в виде многоугольника, вершинами которого являются ненулевые поставки за исключением исходной, для которой делается перераспределение. Стороны контура должны целиком принадлежать одному столбцу или одной строке и могут проходить через ненулевые элементы, не являющиеся вершинами контура. Нумерация вершин начинается с единицы.

В процессе перераспределения минимальный по модулю элемент четных вершин контура прибавляется последовательно к поставкам нечетных и вычитается из поставок четных вершин.

Новые поставки вносятся в очередную версию плана , и процедура определения потенциалов строк и столбцов повторяется с последующим расчетом псевдозатрат для нулевых элементов и проверкой условия оптимальности.

Общий алгоритм решения состоит из предварительного этапа, связанного с нахождением базисного решения в виде исходного опорного плана , и конечного числа итераций перехода от исходного варианта к оптимальному.

Исходный опорный план может быть построен по методу минимального элемента матрицы затрат , при котором последовательно в порядке возрастания выбираются элементы, начиная с минимального и соответственно им распределяются ресурсы поставщиков по удовлетворению запросов потребителей. После проверки невырожденности базисного решения, для очередной итерации рассчитываются потенциалы строк и столбцов и характеристики псевдозатрат. Далее в зависимости от наличия элементов следует либо печать оптимального решения, либо перераспределение поставок.

Задание и порядок выполнения

I. Для заданной матрицы затрат с_ij по перевозкам однородного груза от n поставщиков (a_i, i =1,n) к m потребителям (b_j, j=1,m) методом потенциалов, составить оптимальный план перевозок x_ij по критерию минимума общих затрат

n m

  c_ij x_ij  min

i=1 j=1

Для этого:

1. Методом минимального элемента строки матрицы затрат составить исходный план;

2. Составить уравнения потенциалов и рассчитать значения потенциалов и псевдозатрат;

3. Проверить условие оптимальности и при отрицательной разности затрат и псевдозатрат составить контур перераспределения грузопотоков;

4. Далее повторить процедуру до получения оптимального графика поставок;

5. По заданной блок-схеме алгоритма составить программу, получить оптимальное решение с распечаткой всех промежуточных шагов. пределить все контуры перераспределения поставок.

6. Найти оптимальный план методом аппроксимаций и сопоставить его с предыдущими результатами, полученных методом потенциалов.

Варианты заданий

2.

15	1	22	19	1	20
21	18	11	4	3	20
26	29	23	26	24	20
21	10	3	19	27	20
19	19	19	19	19	20

1.

16	30	17	10	16	4
30	27	26	9	23	6
13	4	22	3	1	10
3	1	5	4	24	10
7	7	7	7	2

4.

20	26	24	26	29	13
15	20	29	26	23	17
4	10	27	60	7	17
9	16	29	20	3	13
12	12	12	12	12

3.

17	20	29	26	25	15
3	4	5	15	24	15
19	2	22	4	13	15
20	27	1	17	19	15
11	11	11	11	16

5

6.

10	17	9	20	30	15
13	4	24	26	26	15
22	24	30	27	29	19
25	12	11	24	23	11
9	24	9	9	9

.

21	22	2	13	7	18
27	10	4	24	9	12
3	16	25	5	4	17
28	11	17	10	29	13
8	8	8	8	28

8.

5	15	3	6	10	9
23	8	13	27	12	11
30	1	5	24	25	14
8	26	7	28	9	16
8	9	13	8	12

7.

30	24	11	12	25	21
26	4	29	20	24	19
27	14	14	10	18	15
6	14	28	8	2	25
15	15	15	15	20

9

10.

30	2	5	6	15	16
5	29	9	5	7	15
16	24	14	6	26	14
13	28	4	25	8	15
6	6	13	20	15

.

9	17	29	28	8	22
13	21	27	16	29	13
20	30	24	7	26	17
11	19	30	6	2	18
7	7	7	7	42

12.

2	24	4	2	31	28
20	10	15	27	7	13
15	15	12	25	19	15
2	6	3	5	5	30
27	16	25	11	7

11.

12	11	25	17	21	17
22	18	14	8	1	14
9	13	2	28	15	21
26	21	3	4	27	43
19	22	23	17	14

1

14.

22	24	25	23	29	24
1	21	10	7	19	14
2	26	18	30	27	19
22	10	29	26	23	17
22	9	12	13	18

3.

15	6	25	11	12	9
13	14	20	27	30	18
16	7	19	10	21	23
1	29	23	25	18	26
11	22	31	6	6	16. 7 10 16 27 19 17 30 18 8 29 15 19 3 18 28 19 13 11 9 12 2 25 21 13 5 15 11 9 20

15.

6	11	20	17	8	12
1	25	3	18	17	17
9	39	16	30	31	18
23	15	4	3	28	13
10	8	12	14	16

1

18.

21	19	11	12	12	24
26	29	14	1	26	12
39	1	22	8	25	18
53	23	40	26	28	16
11	13	26	10	10

7.

5	3	24	10	25	24
30	2	22	16	7	15
30	24	27	29	10	16
15	17	21	2	3	24
12	13	14	31	9

1

20.

14	25	18	19	23	33
2	17	16	24	2	25
29	3	7	15	22	25
5	20	17	23	10	17
33	11	11	11	34

9.

25	28	20	15	7	16
27	5	11	23	10	12
1	25	14	16	16	14
8	6	4	16	18	18
7	8	4	11	30

22.

30	20	27	15	26	33
25	6	28	20	5	33
19	24	11	29	23	33
1	4	6	6	8	11
22	22	22	22	22

21.

8	1	19	1	15	18
8	27	30	7	7	23
10	20	19	26	20	17
18	28	25	7	22	22
21	21	9	9	20

2

24.

29	53	39	29	22	33
15	33	16	3	3	18
16	27	16	3	5	32
35	50	39	20	23	17
20	20	20	20	20

3.

11	10	15	8	7	16
12	14	29	20	20	15
18	7	5	25	28	24
24	4	30	24	26	15
15	15	15	15	10

2

26.

28	26	12	22	11	24
20	23	25	22	9	27
23	15	11	22	7	16
1	26	10	11	19	13
16	16	16	16	16

5.

12	6	29	19	21	13
14	3	30	10	10	27
5	27	28	11	24	16
1	23	25	15	13	14
14	14	14	14	14

28.

20	5	27	10	26	15
7	17	18	21	28	25
27	21	9	23	26	5
1	13	17	23	7	15
7	8	13	12	20

27.

29	4	7	6	16	14
21	13	25	21	7	14
20	10	12	6	2	14
17	7	4	6	19	18
12	12	12	12	12

2

30.

14	5	27	29	23	18
17	7	16	19	2	14
20	12	15	29	5	16
14	24	18	7	13	12
8	11	11	9	21

9.

17	29	2	8	18	32
14	8	25	15	21	8
29	11	15	13	20	13
27	15	19	8	14	27
15	15	15	15	20