Лабораторная работа №3

«Методы многомерной оптимизации в задачах нелинейной аппроксимации» (2 часа).

Цель работы заключается в практическом освоении различных методов безусловной многомерной оптимизации с использованием процедурных модулей одномерной минимизации, в задачах численного анализа факторного пространства.

Постановка задачи

Для задания таблицы значений функции х_i, y_i, i=1,m; и аппроксимирующей функции y = (x,a,b) найти значения а и b по критерию наименьших квдратов.

F(a,b) =

И величину среднеквадратичного отклонения

_________

_ср= F(a,b)/m

Для определения значений параметров а и b , дающих минимум _ср , использовать один из методов безусловной многомерной оптимизации.

Порядок выполнения работ

1. Используя программные модули многомерной оптимизации найти координаты минимума функции F(a,b);

2. Определить величину остаточной дисперсии и среднеквадратичного отклонения расчетных значений от экспериментальных;

3. Выдать на экран таблицу значений полученной функции y = (x,a,b) на отрезке [x₁,x_m] с постоянным шагом h = 0.1 (x_m - x₁);

4. Решить задачу методом наименьших квадратов и сопоставить результаты.

Варианты заданий:

Литература:

1. А. Л. Конин, Н. В. Копченова «Методические указания к практическим занятиям по курсу «Математические методы оптимизации». М. МЭИ,1986. –28с.

Лабораторная работа № 4

«Общая задача линейного программирования» (4-6 часов).

Теоретическое введение

Общая задача линейного программирования связана с нахождением экстремального значения линейной функции n-переменных x₁...x_n

(4-1)

при ограничениях в виде системы линейных относительно x_j; алгебраических уравнений (неравенств)

; (4-2)

и условии

; (4-3)

Введением дополнительных переменных система неравенств приводится к системе линейных уравнений и ОЗЛП представляется в канонической форме:

; (4-4)

Идея метода линейного программирования (ЛП) заключается в направленном переборе вариантов решения с последовательным улучшением, т.е. приближением к максимуму или минимуму. При этом (n-m) -переменных принимают произвольные значения, т.е. являются свободными, а остальные m – переменных становятся базисными и выражаются через свободные системой базисных уравнений.

Величина p = n – m называется степенью неопределенности системы. При степени неопределенности системы не больше двух задача ЛП, записанная в канонической форме, допускает графическое решение на плоскости.

Процедура перехода к новому базису может быть формализована и сведена к заполнению стандартных симплексных таблиц, систематизирующих в матричной форме коэффициенты симплексных уравнений исходного базиса и соответствующего уравнения целевой функции и симплексных таблиц.

Симплексная таблица представляет собой двумерный массив коэффициентов ; ; системы симплексных уравнений, строки которого соответствуют базисным переменным, а столбцы набору базисных и свободных переменных. Последняя строка упорядочивает коэффициенты целевой функции F, а столбец значения базисных переменных в базисном решении. Признаком неоптимальности служит наличие в строке F положительных элементов при отыскании min и отрицательных – при отыскании max.

Если решение неоптимально, о чем свидетельствует наличие положительных элементов в строке коэффициентов целевой функции, составляется другая симплексная таблица, соответствующая улучшенному решению. В этом случае выбирается ключевой вектор-столбец k, соответствующий положительному максимальному коэффициенту в строке F (в случае max-максимальному по модулю отрицательному) целевой функции, и ключевая вектор-строка r с наименьшим положительным частным от деления элементов столбца свободных членов на соответствующие элементы ключевого столбца.

Переход к новому базису связан с введением в него k-й свободной переменной вместо базисной переменной, наиболее близкой к нулю, соответствующей r-й ключевой строке. Исключение из системы k-й переменной и ввод ее в базис вместо , где ; - индексный массив базисных переменных, осуществляется пересчетом симплексной таблицы методом Гаусса - Жордана.

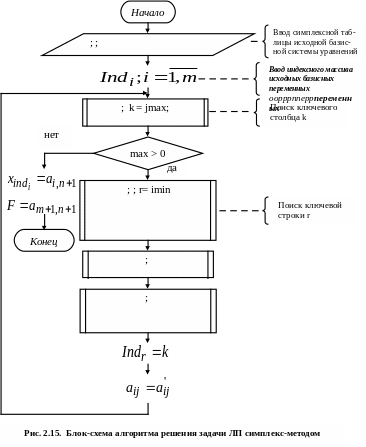
Процесс пересчета повторяется до тех пор пока в строке F не окажется положительных коэффициентов (в случае поиска max - отрицательных). Блок-схема алгоритма нахождения минимума целевой функции приведена на рис.2.15.

Нахождение исходного базисного решения в задачах ЛП представляет собой самостоятельную задачу, т.к. каноническая форма и следующий из нее первоначальный базис далеко не всегда определяет начальную точку области допустимых решений. Так, если в столбце свободных членов симплексной таблицы канонической формы окажется хотя бы один отрицательный элемент, то ограничение ; не выполняется и исходная точка находится вне области допустимых решений. В этом случае процедура формирования исходного опорного базиса сводится к отысканию r-й ключевой строки с максимальным по модулю отрицательным элементом ; и далее в ключевой строке - максимального по модулю отрицательного элемента k-го ключевого столбца.

Далее следует пересчет таблицы коэффициентов методом Гаусса-Жордана.

Задание и порядок выполнения работы

Для заданной целевой функции и системы ресурсных ограничений по переменным х[i], j =1,m и объемам выпуска j-го вида продукции методом линейного программирования найти оптимальную программу выпуска продукции (производственный план) с достижением минимума затрат (максимальной прибыли).

Порядок работы

1. Интерпретировать заданную систему ограничений к задаче оптимального планирования и найти графическое решение построением области допустимых решений.

Для этого:

а) перейти к канонической форме, выбрать свободные переменные и составить систему базисных уравнений;

б) приравняв все переменные к 0, построить границы области на плоскости изменения свободных переменных;

в) по найденной области допустимых решений определить точку исходного базисного решения, ближайшую к канонической форме, но не совпадающую с экстремумом;

г) составить систему симплексных уравнений для исходной точки;

д) для степени неопределенности р = 2 отладить программу симплекс – метода, найти точное решение и сопоставить его с графическим.

2. Для поиска исходного базисного решения:

а) составить симплексную таблицу для исходной канонической формы;

б) проанализировать столбец свободных членов а[i,n+1] и сопоставить с областью допустимых решений (если все элементы положительны, то имеем исходное базисное решение; если нет, то следует пересчет по модулю Basis);

в) составить программу модуля «исходный базис» и включить его в общий алгоритм симплекс – метода.