45

Лабораторный практикум

По курсу «Теория принятия решений» (36 часов)

Специальность 220200

Лабораторная работа №1

«Методы одномерной оптимизации» (2-4 часа).

Теоретическое введение

Задача одномерной оптимизации заключается в нахождении на некотором отрезке [a,b] экстремума (максимума или минимума) непрерывной функции с заданной точностью .

Для определения точки экстремума применяются различные методы, различающиеся стратегиями выбора очередного шага. Поиск заканчивается, когда шаг очередного приближения становится сравним с заданной точностью, т.е. h  . Для определенности будем считать, что речь идет о минимуме функции f(x) на отрезке [a, b].

Метод прямого перебора

Алгоритм поиска экстремума методом прямого перебора заключается в сравнении значений функции y₁, y₂ и y₃ в трех соседних точках x₁, x₂ и x₃ в пределах отрезка [a, b] с шагом изменения h (Рис.1.1).

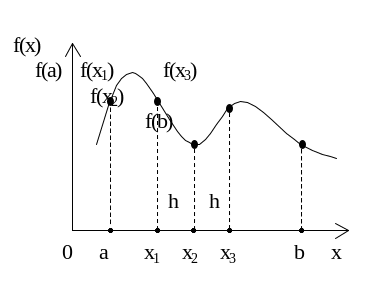
Рис.1.1. Поиск экстремума методом прямого перебора

Значение в точке x₂ сравнивают со значениями в точках x₁ и x₃. Если y₂ меньше y₁ и y₃, то значение y₂ является минимумом y_min. В случае если y₂ больше y₁ и y₃,, то имеет место максимум функции y_max. Далее делается очередной шаг внутрь отрезка [a,b] с повторением процедуры сравнения до границы отрезка.

Метод половинного деления

Метод половинного деления используется для поиска экстремума унимодальной функции, т.е. функции, имеющей на интервале [a, b] один экстремум. Заданный отрезок [a, b] делится пополам (точка c = (a+b)/2 ) и далее в середине одного из полученных отрезков, например, (Рис.1.2 а) отрезка [a,c] определяется точка x1 = (a+c)/2. Затем сравниваются значения целевой функции f(c) и f(x₁), соответственно в точках c и x и если f(x₁) < f(c), то b = c; c = x, иначе определяется точка справа (Рис.1.2 б)

и если f(x₂) < f(с), то а = с; с = х₂ иначе а = х₁; b = x₂.

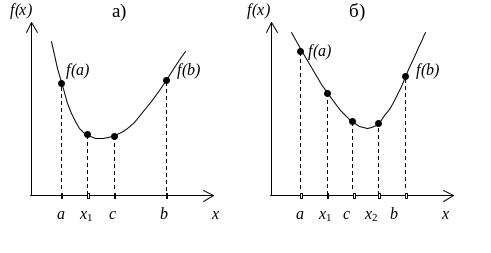
а) б)

Рис. 1.2. Поиск экстремума методом половинного деления

Т.е по результатам сравнения из двух отрезков выбирается отрезок, содержащий экстремум. Поиск завершается при выполнении условия точности

b - a  , где  - малая величина. Блок-схема алгоритма приведена на рис.1.3.

Метод дробного шага

Поиск экстремума методом дробного шага показан на рис.1.4. Сначала задается величина шага h и начальное приближение, например, левая граница отрезка (x = a). В точке начального приближения рассчитывается значение функции

y_m = f(x) и делается шаг в точку x = x + h. Если x > b, то значение x_m = b считается искомым экстремумом и выводится на печать. При x  b проверяется условие h <. и если h  , то при y_m < f(x) шаг уменьшается в 2 раза с изменением направления поиска на противоположное (т.е. h = - h/2). В противном случае y_m = f(x), x_m = x и процедура поиска повторяется.

При h <  вычисленное значение выводится на печать как искомый экстремум.

Рис.1.3. Блок-схема алгоритма метода половинного деления

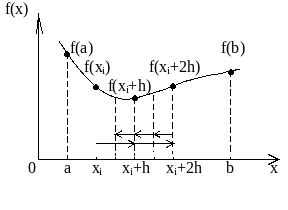
Рис. 1.4. Поиск экстремума методом дробного шага

Блок-схема алгоритма метода дробного шага при отыскании минимума приведена на рис.1.5.

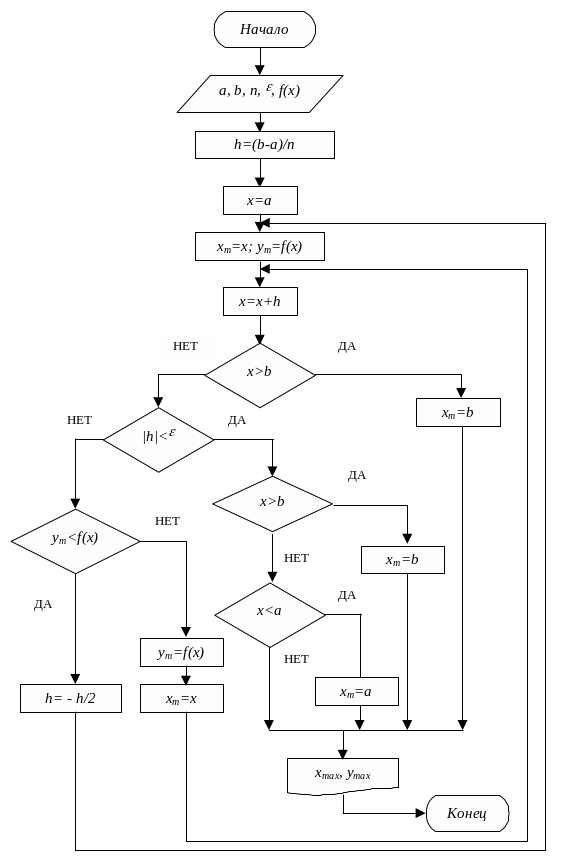
Рис. 1.5. Блок-схема метода дробного шага

Задание и порядок выполнения работы

1. Для заданной целевой функции f(x) составить и реализовать программу табулирования на произвольном отрезке с заданным шагом h.

2. Выделить отрезки, содержащие один или несколько экстремумов, найти экстремальные значения функции методом «прямого перебора» (для нескольких экстремумов), а также методами «половинного деления», «золотого сечения» и «дробного шага» (в случае унимодальной функции).

3. Объединить отдельные программные модули в головную программу EXTR и выдать на экран таблицу результатов по каждому методу.