Вопрос 26

Процесс ортогонализации Грамма-Шмидта

Метод Грамма-Шмидта позволяет ортогонализировать произвольную систему из k линейно независимых векторов. При этом выполняются следующие условия. Если   -исходная система векторов, а      система  полученная в результате процесса ортогонализации, то

1.      Линейная оболочка    совпадает с линейной оболочкой     для   .

2.       ,   где через    обозначаем  - мерный объем   - мерного параллелепипеда  со сторонами   .

Итак,  полагаем   

Предположим, что  векторы     уже построены. Построим вектор  .

Положим     

Числа      находим из условий   для  . Учитывая, что построенные векторы    попарно ортогональны, получаем простейшую систему уравнений для нахождения чисел   :

                                       

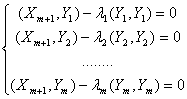
Вычислив значения чисел    находим затем вектор                     .

Используя процесс ортогонализации можно находить k мерные объемы k мерных параллелепипедов, высоты  k мерных параллелепипедов и т.п.

Следующее утверждение легко доказывается   с  помощью метода ортогонализации.

Вопрос 27.

ГРАМА МАТРИЦА

- квадратная матрица 

составленная из попарных скалярных произведений   элементов (векторов) (пред)гильбертова пространства. Г. м. всегда неотрицательна. Она положительно определена, если а ₁, а ₂,..., а _k линейно независимы. Справедливо обратное: любая неотрицательная (положительно определенная) (kx k)-матрица есть нек-рая Г. м. (с линейно независимыми определяющими векторами).

Если   суть га-мерные векторы (столбцы) n-мерного евклидова (эрмитова) пространства собычным скалярным произведением 

то

где Аесть   -матрица, составленная из столбцов  ,   знак ^T означает операцию транспонирования матриц, а черта сверху - взятие комплексно сопряженной величины

Матрицей Грама системы векторов a1…ak называется матрица, i строками которой являются скалярные произведения (ai,a1) (ai,a2)… (ai, ak). Определитель этой матрицы называется определителем Грама.  Теорема. Система векторов линейно зависима тогда и только тогда, когда определитель Грама равен нулю. Док-во. Рассмотрим вектор, являющийся линейной комбинацией векторов системы: y = α1a1 + α2a2..+αkak – равенство его нулю равносильно ортогональности каждому вектору оболочки, натянутой на векторы a1..ak – это равносильно ортогональности каждому вектору системы. Записываем эти условия в систему и получаем, что это выполняется тогда и только тогда, когда определитель матрицы нулевой. Теорема. Матрица Грама системы векторов евклидова (ун) пространства эрмитова. Док-во. Транспонируем, сопрягаем, получаем тож самое. Доказано. Теорема. Определитель Грама линейно независимой системы векторов положителен. Док-во. Пусть а1..аk - лнз система векторов. Выберем ортонормированный базис е1..еk, составим матрицу координат а1..ak в этом базисе, матрица Грама равна (A'A)т, определитель матрицы Грама равен квадрату определителя матрицы А - то есть положителен.