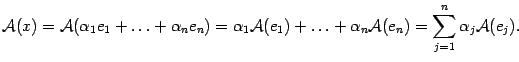Вопрос 12
Матрица линейного преобразования
В примере 19.4 было показано, что преобразование -мерного пространства, заключающееся в умножении координатных столбцов векторов на фиксированную матрицу, является линейным преобразованием. В этом разделе мы покажем, что все линейные преобразования конечномерного пространства устроены таким же образом.
Пусть
--
-мерное
линейное пространство, в котором задан
базис
,
--
линейное преобразование. Возьмем
произвольный вектор
.
Пусть 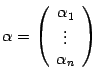 --
его координатный столбец. Координатный
столбец вектора
обозначим
--
его координатный столбец. Координатный
столбец вектора
обозначим ![]() .
.
Запишем
разложение вектора
по
базису пространства ![]() .
Для образа этого вектора получим
.
Для образа этого вектора получим
|
(19.2) |
Векторы ![]() имеют
какие-то координатные столбцы, обозначим
их
имеют
какие-то координатные столбцы, обозначим
их 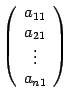 ,
, 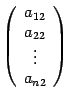 ,
...,
,
..., 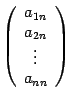 соответственно.
В этой записи первый индекс показывает
номер координаты, а второй индекс --
номер вектора. Соответственно,
соответственно.
В этой записи первый индекс показывает
номер координаты, а второй индекс --
номер вектора. Соответственно,
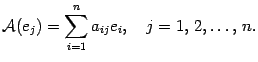
Подставим это выражение в равенство (19.2) и, используя предложение 14.3, изменим порядок суммирования
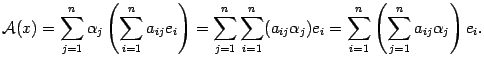
Это
равенство означает, что
-той
координатой вектора
служит 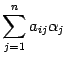 .
.
Составим
матрицу ![]() из
координатных столбцов векторов
из
координатных столбцов векторов ![]() ,
...,
,
..., ![]()
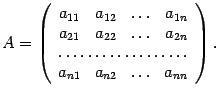
Вычислим произведение матрицы на столбец
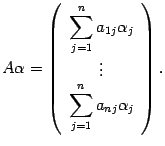
Мы видим, что -ый элемент столбца совпадает с -ой координатой вектора . Поэтому
|
(19.3) |
Это означает, что в выбранном базисе действие любого линейного преобразования сводится к умножению матрицы на координатный столбец вектора.
Матрица называется матрицей линейного преобразования . Еще раз напомним, как она составлена: первый столбец является координатным столбцом образа первого базисного вектора, второй столбец -- координатным столбцом образа второго базисного вектора и т.д.
Пример 19.5 Найдем матрицу линейного преобразования из примера 19.1.
Выберем
какой-нибудь базис ![]() .
Тогда
.
Тогда
![]()
Следовательно,
первый столбец матрицы
имеет
вид 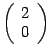 .
Аналогично
.
Аналогично
![]()
Второй
столбец матрицы
имеет
вид 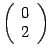 .
В итоге
.
В итоге
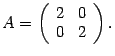
Пример 19.6
Найдем матрицу линейного преобразования
из
примера
19.2.
Угол ![]() возьмем
равным
возьмем
равным ![]() .
В качестве базиса возьмем привычный
ортонормированный базис i, j.
.
В качестве базиса возьмем привычный
ортонормированный базис i, j.
Из
рисунка 19.7 видно, что вектор ![]() имеет
координаты
имеет
координаты ![]() и
и ![]() .
.
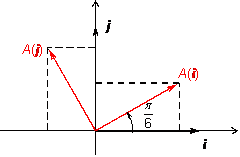
Рис.19.7.Координаты образов базисных векторов при преобразовании поворота
Поэтому
координатный столбец образа первого
базисного вектора имеет вид 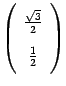 .
Координаты образа второго базисного
вектора равны
.
Координаты образа второго базисного
вектора равны ![]() и
и ![]() ,
его координатный столбец имеет вид
,
его координатный столбец имеет вид 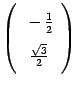 .
В итоге получаем, что в базисе i, j матрица
поворота на угол
имеет
вид
.
В итоге получаем, что в базисе i, j матрица
поворота на угол
имеет
вид
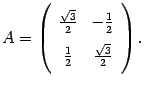
Вопрос №13.
Пусть L -- n -мерное линейное пространство, и e1,…,en и e1’,…,en’ -- два базиса в этом пространстве. Первый из них назовем "старым", а второй -- "новым". Пусть S -- матрица перехода а от старого базиса к новому.
Предложение 19.1
Пусть A -- линейное
преобразование пространства L
, и A и A’
-- матрицы этого преобразования в старом
и новом базисе соответственно. Тогда
A’=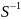 AS
AS
Доказательство. Пусть x -- произвольный вектор пространства L , y -- его образ, то есть y=A(x) . Пусть α и β -- координатные столбцы векторов x и y в старом базисе, а x’, y’ -- в новом. Тогда в силу формулы β=Aα имеем α=Sα’ , β=Sβ' . Подставим эти выражения в предыдущую формулу, получаем Sβ’=A(Sα’) . Откуда β’=( AS)α’ . С другой стороны, в силу формулы β=Aα в новом базисе β’=A’α’ . Сравнивая это равенство с предыдущим, получаем A’= AS .
Определение Две квадратных матрицы P и Q одного порядка называются подобными, если существует такая невырожденная матрица S , что P= QS .
Следствие Матрицы одного линейного преобразования, соответствующие разным базисам, подобны друг другу, и наоборот, если матрицы подобны, то они являются матрицами одного и того же преобразования в разных базисах.
Вопрос №14.
Вектор х называется собственным вектором матрицы А, если найдется такое число λ, что выполняется равенство: Ах = λх. Само число λ называется собственным числом матрицы А.
Для произвольного вектора х =х1е1 + х2е2 + х3е3 результатом применения к нему линейного преобразования А будет вектор Ах, который можно разложить по векторам того же базиса: Ах =х`1е1 + х`2е2 + х`3е3, где координаты x`i можно найти по формулам:
х`1 = a11x1 + a12x2 + a13x3
x`2 = a21x1 + a22x2 + a23x3,
x`3 = a31x1 + a32x2 + a33x3.
Коэффициенты в формулах этого линейного преобразования являются элементами строк матрицы А.
Подставив в формулы (9.3) x`j = λxj, получим систему уравнений для определения координат собственного вектора:
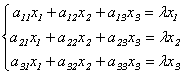
Отсюда
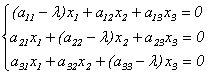
Эта линейная однородная система будет иметь нетривиальное решение только в случае, если ее главный определитель равен 0 (правило Крамера). Записав это условие в виде:
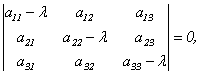
получим уравнение для определения собственных чисел λ, называемое характеристическим уравнением. Кратко его можно представить тaк: | A - λE | = 0
Вопрос №15.
Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.
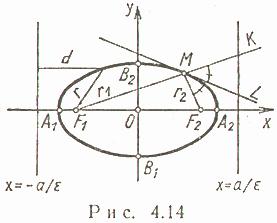
Обозначим фокусы через F1 и F2 ,расстояние между ними через 2с, а сумму расстояний от произвольной точки эллипса до фокусов — через 2а
По определению 2а > 2с, т.е. a > с.
Для вывода уравнения эллипса выберем систему координат Оху так, чтобы фокусы F1 и F2 лежали на оси Ох, а начало координат совпадало с серединой отрезка F1F2 . Тогда фокусы будут иметь следующие координаты:
![]() и
и
![]()
Пусть М(х;у)
— произвольная точка эллипса. Тогда,
согласно определению эллипса,![]() , т. е.
, т. е.![]()
Это, по сути, и есть уравнение эллипса.
Преобразуем уравнение к более простому виду:
![]()
![]()
![]()
![]()
![]()
Так как a
> с, то
![]() Положим
Положим
![]() Тогда
последнее уравнение примет вид
Тогда
последнее уравнение примет вид
![]() или
или
![]()
16
Гипербола
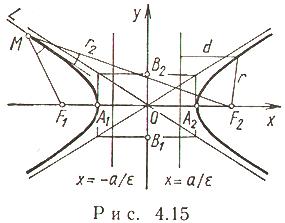
Пусть
на плоскости заданы две точки ![]() и
и ![]()
![]() и
дано число a
(0 < a < c). Гипербола - множество
точек M плоскости,
для каждой из которых модуль разности
расстояний от точек
и
равен 2a.
Точки
и
называются
фокусами гиперболы;
и
дано число a
(0 < a < c). Гипербола - множество
точек M плоскости,
для каждой из которых модуль разности
расстояний от точек
и
равен 2a.
Точки
и
называются
фокусами гиперболы; ![]() -
действительная ось;
-
действительная ось; ![]() -
мнимая ось; O -
центр;
-
мнимая ось; O -
центр; ![]() -
левый и правый фокусы;
-
левый и правый фокусы; ![]() -
вершины;
-
вершины; ![]() -
фокальные радиусы:
-
фокальные радиусы: ![]()
Каноническое
уравнение: 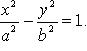
Эксцентриситет: 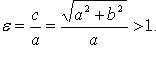
17
Парабола
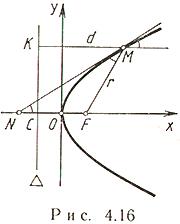 Пусть
на плоскости заданы точка F и
прямая
Пусть
на плоскости заданы точка F и
прямая ![]() ,
не проходящая через F.
Парабола - множество всех тех
точек M плоскости,
каждая из которых равноудалена от
точки F и
прямой
.
Точка F называется
фокусом, прямая
-
директрисой параболы; (OF) -
ось, O -
вершина,
,
не проходящая через F.
Парабола - множество всех тех
точек M плоскости,
каждая из которых равноудалена от
точки F и
прямой
.
Точка F называется
фокусом, прямая
-
директрисой параболы; (OF) -
ось, O -
вершина, ![]() -
параметр,
-
параметр, ![]() -
фокус,
-
фокус, ![]() -
фокальный радиус.
-
фокальный радиус.
Каноническое
уравнение: ![]()
Эксцентриситет: 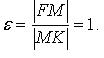
18
Эллипс:
К ним
относят:
число a, называемые большой
полуосью;
число b, называемое малой
полуосью;
число ![]() ,
называемое линейным эксцентриситетом;
число 2с, называемое фокусным
расстояние;
число
,
называемое линейным эксцентриситетом;
число 2с, называемое фокусным
расстояние;
число ![]() ,
называемое (числовым ) эксцентриситетом
(0 ≤ ε < 1);
число p = b² / a, называемое фокальным
параметром;
ось абсцисс, называемая большой (или
фокальной) осью;
ось
ординат, называемая малой осью;
точка О(0, 0), называемая центром;
точки (а, 0) и (-а, 0), (0, b) и (0, -b),
называемые вершинами;
точки (-с, 0) и (с, 0), называемые фокусами;
при ε ≠ 0 прямые x = a / ε и x = -a / ε,
называемые директрисами.
Фокус (с, 0) и директриса x = a / ε
называются правыми, а фокус (-с, 0) и
директриса x = -a / ε - левыми. Фокус
и директриса называются одноименными,
если они оба - правые или оба - левые. Это
отношение между фокусом и директрисой
геометрически инвариантно, тогда как
свойство фокуса (директрисы) быть правым
или левым зависит от ориентации оси
абсцисс.
Для окружности b = a, c = 0, ε = 0, p = a, фокусы
совпадают с центром, а директрисы не
определены.
,
называемое (числовым ) эксцентриситетом
(0 ≤ ε < 1);
число p = b² / a, называемое фокальным
параметром;
ось абсцисс, называемая большой (или
фокальной) осью;
ось
ординат, называемая малой осью;
точка О(0, 0), называемая центром;
точки (а, 0) и (-а, 0), (0, b) и (0, -b),
называемые вершинами;
точки (-с, 0) и (с, 0), называемые фокусами;
при ε ≠ 0 прямые x = a / ε и x = -a / ε,
называемые директрисами.
Фокус (с, 0) и директриса x = a / ε
называются правыми, а фокус (-с, 0) и
директриса x = -a / ε - левыми. Фокус
и директриса называются одноименными,
если они оба - правые или оба - левые. Это
отношение между фокусом и директрисой
геометрически инвариантно, тогда как
свойство фокуса (директрисы) быть правым
или левым зависит от ориентации оси
абсцисс.
Для окружности b = a, c = 0, ε = 0, p = a, фокусы
совпадают с центром, а директрисы не
определены.
Гипербола:
Фокальные радиусы:
для
правой ветви ![]()
для
левой ветви ![]()
Фокальный
параметр: ![]()
Уравнения
директрис: ![]()
Парабола:
Фокальный
радиус: ![]()
Уравнение
директрисы: ![]()
Уравнение
касательной в точке ![]()
![]()