4. Оценка точности при стационарных случайных воздействиях
При случайных воздействиях F(t) или Yз(t) точность оценивается средним квадратом ошибки:
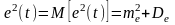, (2.15.17)
где me среднее значение ошибки; De дисперсия ошибки.
В случае центрированного случайного процесса точность оценивается только дисперсией De.
5. Устойчивость это свойство системы возвращаться в исходный или близкий к нему установившийся режим после снятия воздействия, вызвавшего выход из установившегося режима.
Выходная величина устойчивой системы остается ограниченной в условиях действия на систему ограниченных по величине воздействий.
Неустойчивая система является неработоспособной, поэтому проверка устойчивости является обязательным этапом анализа системы, а обеспечение устойчивости обязательным условием синтеза.
В общем случае качество нелинейных систем зависит от величины воздействий. Системы устойчивые при одних воздействиях могут быть неустойчивы при других воздействиях. В связи с этим существуют понятия устойчивости в малом, в большом и в целом (абсолютная устойчивость).
Устойчивость в малом устойчивость при бесконечно малых отклонениях от исходного режима.
Устойчивость в большом устойчивость при конечных отклонениях от исходного режима, возможных в данной системе по условиям работы.
Устойчивость в целом устойчивость при неограниченных отклонениях.
В линейных системах таких градаций устойчивости не существует. Линейная система либо неустойчива, либо находится на границе устойчивости, либо устойчива в целом. При этом будут устойчивы не только положения равновесия системы, но и любые вынужденные процессы.
Движение системы имеет две составляющие:
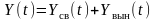, (2.16.1)
где
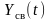
свободная составляющая движения, когда
воздействия на систему отсутствуют;Yвын
вынужденная составляющая установившегося
движения системы при наличии воздействия.
Из определения устойчивости, следует, что у устойчивых систем свободная составляющая затухает.
Рассмотрим условие устойчивости линейных систем.
Решение Yсв(t) однородного дифференциального уравнения имеет вид:
, (2.16.2)
где постоянные интегрирования, определяющиеся начальными условиями и возмущением; рi корни характеристического уравнения.
Комплексным корням рi соответствуют колебательные переходные процессы, действительным корням рi апериодические переходные процессы.
Для того чтобы свободная составляющая затухала (система была устойчива), действительные части всех корней рi должны быть отрицательными. Если хотя бы один из корней имеет действительную положительную часть, то система неустойчива. Если все корни рi мнимые, то система находится на границе устойчивости.
Изобразим корни на комплексной плоскости и получим следующее правило. Устойчивой системе соответствуют левые корни характеристического уравнения, неустойчивой правые.
Поскольку решение уравнений высокого порядка сопряжено с определенными трудностями, то анализ устойчивости линейных систем проводится по алгебраическим и частотным критериям. Наиболее часто используют алгебраический критерий Гурвица и частотный критерий Найквиста.