4. Понятие о моментах инерции твёрдых тел, их вычисление.
Моменты инерции – это величины, характеризующие распределение массы по объёму, занимаемому твердым телом.
Моменты инерции бывают полярными, осевыми и центробежными. Подробно будут рассмотрены лишь осевые моменты инерции.
Рассмотрим
механическую систему (или твёрдое тело)
и проведём какую-либо ось
.
Обозначая
через
расстояние от проведённой оси до точки
с массой
,
введём величину
2525\* MERGEFORMAT ()
равную сумме произведений масс всех точек системы на квадраты их расстояний до оси.
Эта введённая величина и называется осевым моментом инерции системы.
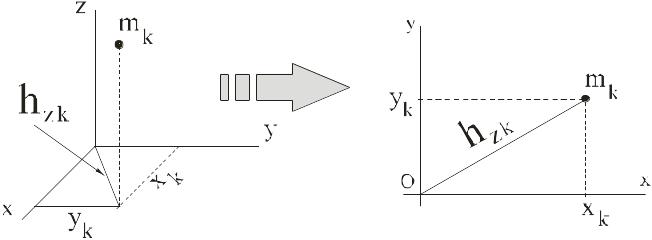
Из определения (25) видно, что
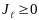
и
обращается в нуль только, если все точки
системы лежат на оси
.
Размерность момента инерции согласно
(25) в систем СИ
.
Осевой момент инерции характеризует распределение массы системы относительно оси: если все точки отодвинуть от оси, в два раза увеличив расстояния, то согласно (25) момент инерции увеличится в четыре раза и т.п.
На
практике чаще требуется определять
моменты инерции не относительно
произвольной оси, а относительно
координатных осей
.
Если положения точек системы заданы
координатами
,
то из (25) следует
2626\* MERGEFORMAT ()
Совершенно аналогично для двух других координатных осей получим:
2727\* MERGEFORMAT ()
Т.к. согласно (25) моменты инерции суть неотрицательные величины, то их можно записать в виде
2828\* MERGEFORMAT ()
где
– масса всей системы (или тела), а
– радиус
инерции системы
(или тела) относительно оси. Из (28) сразу
виден физический смысл радиуса инерции:
радиус инерции системы – это такое расстояние от оси, на котором нужно сосредоточить всю массу системы, чтобы момент инерции полученной точки относительно оси был равен моменту инерции системы.
Из (28) следует
2929\* MERGEFORMAT ()
При вычислении моментов инерции твёрдых тел вместо сумм во всех формулах следует вычислять интегралы по объёму тела
где
плотность тела в данной точке. Поэтому
вычисление моментов инерции произвольных
тел представляет достаточно сложную
задачу. Для часто встречающихся на
практике тел (шары, конусы, параллелепипеды,
цилиндры и пр.) моменты инерции
относительно центральных осей (т.е.
осей, проходящих
через центр масс тела)
приводятся в справочниках. Для простейших
однородных тел моменты инерции могут
быть непосредственно вычислены по
приведенной выше формуле.
Запишем без вывода моменты инерции некоторых простейших тел, с которыми будем иметь дело на практике.
1) Тонкое однородное кольцо массы m и радиуса R.
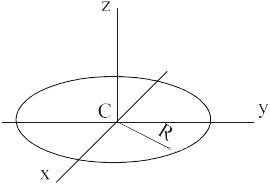
2) Тонкий однородный диск массы m и радиуса R.
3) Тонкий однородный стержень массы m и длины .
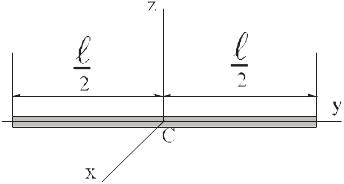
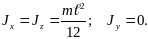
Как уже было отмечено, в справочниках моменты инерции тел приводятся для центральных осей. Но при решении задач иногда нужно определять моменты инерции относительно других осей. В частности, – относительно осей, параллельных центральным.
Получим формулы, связывающие моменты инерции относительно параллельных осей.
Пусть
известны моменты инерции относительно
центральных осей:
.
Нужно определить моменты инерции
относительно осей Oxyz,
параллельных центральным осям:
.
Имеем по определению
Но ясно, что для координат точек справедливы соотношения
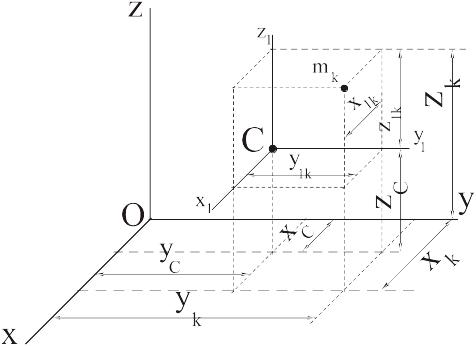
Тогда
Далее
это
момент инерции относительно центральной
оси
;
произведение
массы тела на квадрат расстояния между
осями
и
,
;
В результате окончательно получаем
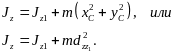3030\* MERGEFORMAT ()
Равенство (30) называют формулой Штейнера-Гюйгенса. Эта формула выражает теорему Штейнера:
момент инерции относительно произвольной оси равен моменту инерции относительно параллельной ей центральной оси сложенному с произведением массы тела на квадрат расстояния между осями.
Для двух других осей точно так же можно получить аналогичные формулы:
Рассмотрим
пример применения формулы Штейнера.
Найдём момент
инерции тонкого однородного стержня
относительно оси
,
проходящей через конец стержня,
перпендикулярно к нему.
По формуле Штейнера-Гюйгенса получаем
Ещё
один пример. Тело
состоит из тонкого однородного стержня
массы m
и длины
и однородного диска массы 2m
и радиуса R.
Найти момент инерции этого тела
относительно оси Oz,
проходящей через конец стержня
перпендикулярно к нему и к плоскости
диска.
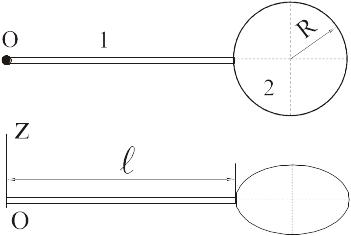
По определению момента инерции имеем
С помощью (29) можно найти радиус инерции этого тела относительно оси Oz:
С помощью формулы Штейнера-Гюйгенса можно установить важное свойство экстремальности моментов инерции:
среди множества моментов инерции тела относительно параллельных осей момент инерции относительно центральной оси принимает наименьшее значение.
Иными словами, если какое-то тело относительно центральной оси имеет момент инерции, равный
то
– это самый маленький момент инерции
среди всех параллельных осей, и ни для
какой из этих осей у тела не может быть
момента инерции, равного, например,
.
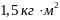Доказательство этого факта очень простое: из формулы Штейнера сразу следует
что и доказывает свойство экстремальности.