Лекция 3

Теорема об изменении количества движения системы.

Кинетический момент системы.

Вопросы лекции.

1. Количество движения точки и системы, импульс силы.

2. Теорема об изменении количества движения системы. Закон сохранения количества движения.

3. Момент количества движения точки и кинетический момент системы и твёрдого тела.

4. Понятие о моментах инерции твёрдых тел, их вычисление.

1. Количество движения точки и системы, импульс силы.

Пусть точка массы m движется в заданной системе координат по закону

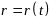11\* MERGEFORMAT ()

и имеет в данный момент времени скорость

22\* MERGEFORMAT ()

Тогда

количеством движения точки называется вектор, равный произведению массы точки на её скорость:

33\* MERGEFORMAT ()

Согласно (3) вектор количества движения направлен вдоль скорости, т.е. по касательной к траектории точки, а модуль количества движения отличается от модуля скорости только скалярным множителем – массой точки m. Поэтому проекции количества движения точки на оси декартовой системы координат Oxyz определятся согласно равенствам:

44\* MERGEFORMAT ()

а модуль

55\* MERGEFORMAT ()

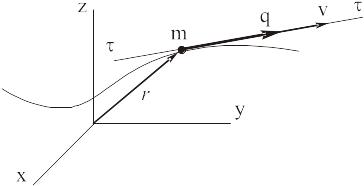
Переходим теперь к движению механической системы.

Для каждой точки системы по формуле (3) считаем вектор количества движения

переносим параллельно полученные векторы в центр О и складываем. Получаем вектор

66\* MERGEFORMAT ()

называемый

главным вектором количеств движения системы,

или, просто,

количеством движения системы.

Согласно выражениям (4) и (5) можно найти проекции на оси и модуль количества движения системы.

Но если вспомнить формулу (21) прошлой лекции:

то равенство (6) можно записать так

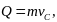77\* MERGEFORMAT ()

т.е. количество движения системы можно вычислять как произведение массы всей системы на скорость её центра масс.

Таким образом, при любом движении твёрдого тела

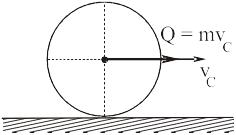
его количество движения определится по формуле (7). В частности, при любом качении однородного колеса (со скольжением, или, без скольжения) по плоскости его количество движения равно произведению массы колеса на скорость его центра.

Если тело совершает вращательное движение

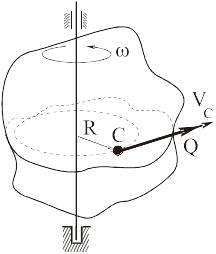
то

Отсюда следует, что если центр масс вращающегося тела находится на оси вращения

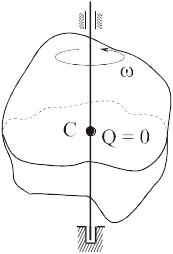
то

Рассмотрим движение точки под действием силы .

Произведение

называют средним импульсом силы за промежуток времени . Если в этом равенстве перейти к пределу при , то получим величину

88\* MERGEFORMAT ()

называемую элементарным импульсом силы.

Если точка под действием силы движется из положения М₀ в положение М₁

то, разбивая траекторию на малые участки, вычисляя на каждом из них средние импульсы и складывая, получим

и, переходя к пределу при , получим вектор

99\* MERGEFORMAT ()

называемый импульсом силы за промежуток времени , или, просто, – импульсом силы.

Согласно (9) для определения проекций импульса силы на какие-либо оси нужно вычислять интегралы от соответствующих проекций силы

1010\* MERGEFORMAT ()

Затем может быть найден модуль импульса

1111\* MERGEFORMAT ()

Рассмотрим примеры.

1) Вектор силы, действующей на точку, определён равенством

Вычислить импульс этой силы за промежуток времени от 0 до 2 с и найти модуль этого импульса.

РЕШЕНИЕ. По формуле (9) получаем

Таким образом, . Поэтому

Можно было бы сразу найти , а затем по формулам (10) вычислить

Тогда .

2) проекция на ось x силы, действующей на точку, задается равенством

Найти проекцию импульса силы на ось x за промежуток от 0 до с.

РЕШЕНИЕ. По первой из формул (10) получим