4. Центр масс механической системы и его определение.

На движение механических систем влияет не только масса всей системы, но и то, как масса распределена по объёму, занимаемому системой в пространстве. Одной из характеристик распределения массы является центр масс.

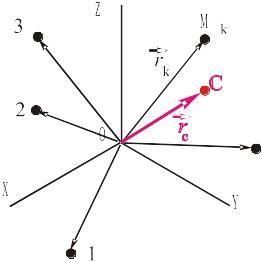
Центром масс механической системы называется такая точка С, радиус-вектор которой определяется по формуле

1717\* MERGEFORMAT ()

Сумма масс всех точек системы

1818\* MERGEFORMAT ()

называется массой системы. Поэтому равенство (17) можно записать так:

1919\* MERGEFORMAT ()

Проектируя выражения (17) или (19) на выбранные оси координат, получим формулы для определения координат центра масс:

2020\* MERGEFORMAT ()

Если точки механической системы движутся, т.е. , то из (17), или (19), следует, что и , вообще говоря, 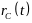. Тогда, дифференцируя по времени (19), можем найти скорость центра масс

2121\* MERGEFORMAT ()

и его ускорение

2222\* MERGEFORMAT ()

С помощью (20) можно найти проекции скорости и ускорения центра масс на оси координат.

Для произвольных механических систем положение центра масс находится по формулам(17), или (19) (координаты – по формулам (20)). Для твёрдых тел в этих равенствах вместо сумм должны стоять интегралы, но можно непосредственно установить положение центра масс тела. Домножим обе части (19) на ускорение свободного падения:

и вспомним, что , тогда

а эта формула для определения центра тяжести твердого тела. Следовательно, центр масс тела всегда совпадает с центром тяжести этого тела!

5. Теорема о движении центра масс и закон сохранения движения центра масс.

Запишем дифференциальные уравнения движения механической системы (13):

Почленно сложим все уравнения:

Имеем:

главный вектор внешних сил;

главный вектор внутренних сил, равный нулю;

где 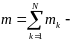масса вей системы. В результате получим:

2323\* MERGEFORMAT ()

Если теперь сравнить равенство (23) с дифференциальным уравнением движения материальной точки

то получим

теорему о движении центра масс механической системы

Центр масс механической системы движется как материальная точка, в которой сосредоточена вся масса системы и к которой приложены все внешние силы.

Уравнение (23) называют дифференциальным уравнением движения центра масс. В проекциях на оси координат Oxyz (23) запишется

2424\* MERGEFORMAT ()

Закон сохранения движения центра масс.

Пусть внешние силы, действующие на систему таковы, что (силы приводятся к паре сил, или уравновешены). В этом случае из (23), учитывая, что , будет следовать

2525\* MERGEFORMAT ()

т.е. центр масс в этом случае движется прямолинейно и равномерно (если ), или находится в покое (если ). Это и есть закон сохранения движения центра масс системы:

если главный вектор внешних сил равен нулю, то центр масс системы движется равномерно и прямолинейно, или находится в покое.

На практике закон сохранения в виде (25) выполняется не слишком часто. Чаще возникает такая ситуация:

Тогда из (24) получим ( )

2626\* MERGEFORMAT ()

что будет частным случаем закона сохранения движения центра масс:

если проекция главного вектора внешних сил на какую-либо ось равна нулю, то центр масс системы относительно этой оси движется равномерно (если ), или находится в покое (если ).

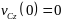Пусть . Следовательно, из закона сохранения можем получить

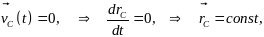
т.е. центр масс системы неподвижен.

Пусть в момент t положения точек системы определяются радиус-векторами , а в момент радиус-векторами .

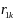По формуле (19) имеем:

в момент

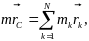
а в момент

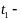
Вычитая из второго равенства первое получим

но это перемещения точек системы за промежуток . Поэтому получаем такой результат:

2727\* MERGEFORMAT ()

если главный вектор внешних сил равен нулю и центр масс системы неподвижен, то сумма произведений масс точек системы на их перемещения равна нулю.

Для частного случая (26) будет

если .

24