Лекция 2
Динамика относительного движения точки.
Дифференциальные уравнения движения
механической системы. Центр масс механической системы.
Вопросы лекции.
1. Дифференциальное уравнение движения точки в неинерциальной системе отсчёта.
2. Уравнение относительного покоя точки.
3. Внешние и внутренние силы. Дифференциальные уравнения движения механической системы.
4. Центр масс механической системы и его определение.
5. Теорема о движении центра масс и закон сохранения движения центра масс.
1. Дифференциальное уравнение движения точки в неинерциальной системе отсчёта.
Основной закон динамики
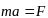
и вытекающее из него дифференциальное уравнение движение точки
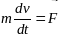
справедливы только в инерциальных системах отсчета. Однако, часто возникает необходимость в исследовании движения точки под действием сил относительно неинерциальных осей координат.
Неинерциальной является, например, система координат, связанная с поверхностью Земли, поскольку она участвует во вращательном движении Земли вокруг оси и, кроме того, – в движении Земли вокруг Солнца.
Пусть
имеется инерциальная система координат
OXYZ,
относительно которой произвольным
образом (как твёрдое тело) движется
подвижная система oxyz.
Точка М массы m движется под действием
силы
.
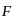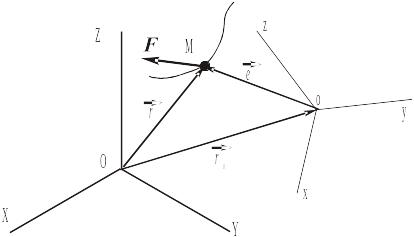
Требуется найти закон её движения (т.е. решить вторую задачу динамики) относительно системы oxyz. Т.к. эта система движется произвольным образом, то можно предположить, что она является неинерциальной. Следовательно, для решения задачи нельзя применить основной закон динамики.
Рассмотрим движение точки в инерциальной системе OXYZ. Тогда справедлив основной закон динамики
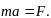
Вспомнив сложное движение точки, можем записать
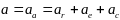
Подставляем в основной закон
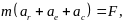
раскрываем скобки
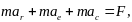
переносим
слагаемые
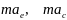в правую часть равенства и получаем
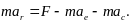11\* MERGEFORMAT ()
В
(1) слагаемые
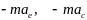имеют размерности сил
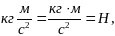
поэтому их назвали соответственно переносной и кориолисовой силами инерции. Обозначения:
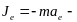22\* MERGEFORMAT ()
–сила инерции переносного движения (переносная сила инерции);
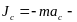33\* MERGEFORMAT ()
– сила инерции Кориолиса (кориолисова сила инерции).
Из равенств (2) и (3) следует, что модули сил инерции равны соответственно
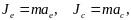
а направления противоположны к направлениям соответствующих ускорений:
В случае кориолисовой силы инерции её направление более подробно может быть определено по относительной скорости:
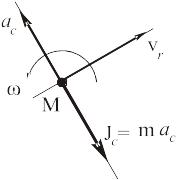
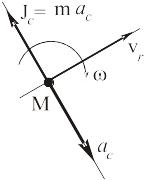
С учётом введённых обозначений равенство (1) запишется в виде
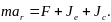44\* MERGEFORMAT ()
Выражение (4) является основным законом динамики для неинерциальных систем:
произведение массы точки на её ускорение в неинерциальной системе равно сумме всех активных сил и реакций отброшенных связей, к которым должны быть добавлены переносная и кориолисова силы инерции.
Т.к.
относительное ускорение точки – это
локальная производная от относительной
скорости, то, обозначая (только в данном
вопросе!!) локальную производную обычным
образом, а относительную скорость –
просто
,
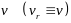получим из (4)
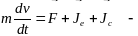55\* MERGEFORMAT ()
дифференциальное уравнение относительного движения точки.
Согласно (2) и (3), для нахождения сил инерции нужно знать переносное и кориолисово (поворотное) ускорения точки. Эти ускорения определяются по формулам сложного движения точки:
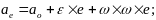66\* MERGEFORMAT ()
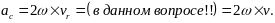77\* MERGEFORMAT ()
Здесь:
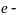относительный радиус-вектор точки,
;
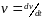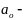ускорение
начала подвижной системы координат
oxyz;
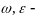угловая скорость и угловое ускорение
подвижной системы.
