4. Принцип возможных перемещений.

Принцип возможных перемещений является необходимым и достаточным условием равновесия механической системы. Его можно использовать вместо векторных условий равновесия (главный вектор и главный момент системы сил равны нулю). Принцип возможных перемещений при изучении равновесия системы тел (составных конструкций) позволяет избежать определения многочисленных внутренних сил и более рационально определить требуемые внешние силы. Принцип возможных перемещений в современном виде был сформулирован Лагранжем, поэтому его иногда называют принципом Лагранжа.

Для равновесия механической системы с идеальными удерживающими связями необходимо и достаточно, чтобы сумма виртуальных работ сил, действующих на систему, на любых возможных перемещениях была равна нулю.

(Без доказательства)

Символически принцип возможных перемещений может быть записан в виде

3232\* MERGEFORMAT ()

Рассмотрим пример применения принципа возможных перемещений к решению задач на равновесие.

Пример. Подъёмное устройство состоит из ведущего колеса 1 радиуса R₁, взаимодействующего с ним ведомого колеса радиуса R₂. На ворот ведомого колеса радиуса r намотана невесомая и нерастяжимая верёвка, к которой привязан поднимаемый груз весом P.

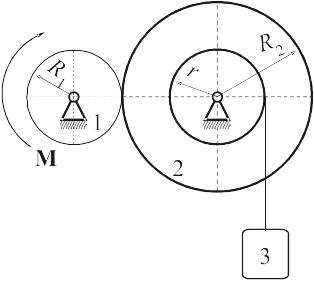
Определить момент М пары сил, которую надо приложить к ведущему колесу, для равномерного подъёма груза. Трением в опорах пренебречь. Скольжение между колесами отсутствует.

РЕШЕНИЕ. Связи являются идеальными, поэтому их реакции не показываем. Изображаем силу тяжести груза и пару сил с искомым моментом. Сообщаем точкам системы возможные перемещения:

поворачиваем колесо 1 на бесконечно малый угол по направлению пары сил;

колесо 2 повернётся при этом на бесконечно малый угол ;

груз 3 сместится вверх на бесконечно малую величину .

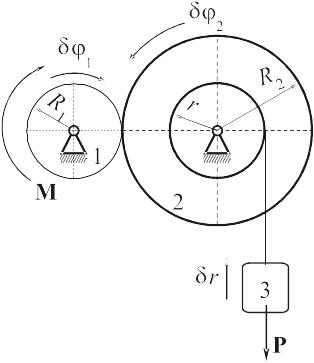
Так как система находится в равновесии, то (принцип возможных перемещений!) сумма виртуальных работ всех сил на любых возможных перемещениях равна нулю:

3333\* MERGEFORMAT ()

На систему наложены связи:

т.к. колеса не скользят относительно друг друга;

т.к. верёвка не растяжимая и не скользит по вороту.

Число координат, определяющих положение системы равно трём: . Число наложенных связей равно двум. Следовательно, число степеней свободы согласно (27) равно , а поэтому у системы только одно независимое возможное перемещение.

Из первой связи получаем

Вторая связь даёт

Подставляя это выражение в сумму виртуальных работ (33), получим

Так как , то

28