III. Геометрические и кинематические.

Связь называется геометрической, если в её аналитическое выражение входят только координаты точек системы.

Связь называется кинематической, если в её аналитическое выражение входят как координаты, так и производные от координат точек.

В примерах А) – D) все связи геометрические. В примерах E), F) приводятся кинематические связи.

Некоторые кинематические связи можно интегрированием привести к геометрическим, а другие – нельзя.

Например, связь (24) (пример Е)) можно привести к геометрической связи:

Связь же (25) из примера F) невозможно с помощью интегрирования привести к геометрической.

IV. Голономные и неголономные.

Голономными называются любые геометрические и кинематические интегрируемые связи.

Кинематические неинтегрируемые связи называют неголономными связями.

В название связи включают её принадлежность по всем четырём критериям классификации. Например, связь

это кинематическая, голономная, стационарная, удерживающая связь.

Связь

это геометрическая (голономная), нестационарная удерживающая связь.

3. Действительные и возможные перемещения.

Пусть точка движется под действием силы . На точку наложена стационарная геометрическая связь

Проинтегрировав дифференциальное уравнение движения точки, можем найти в каждый момент времени

Отсюда

2626\* MERGEFORMAT ()

Равенство (26) определяет бесконечно малое перемещение точки за промежуток времени . Это перемещение удовлетворяет уравнению связи, происходит в результате действия на точку приложенных сил и называется действительным перемещением точки.

Однако, в данный момент времени связь не нарушится (т.е. точка останется на поверхности, определяемой уравнением связи), если точке сообщить некоторые бесконечно малые перемещения, отличные от действительного.

Такие бесконечно малые перемещения называют возможными перемещениями.

Любое бесконечно малое перемещение, не нарушающее в данный момент времени наложенных связей, называется возможным перемещением.

Возможные перемещения, чтобы отличить их от действительных, принято обозначать через .

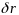В отличие от действительных возможные перемещения совершаются при фиксированном времени, т.е. точки системы могли бы переместиться без нарушения наложенных связей. Для различных моментов времени t множества возможных перемещений, вообще говоря, различны.

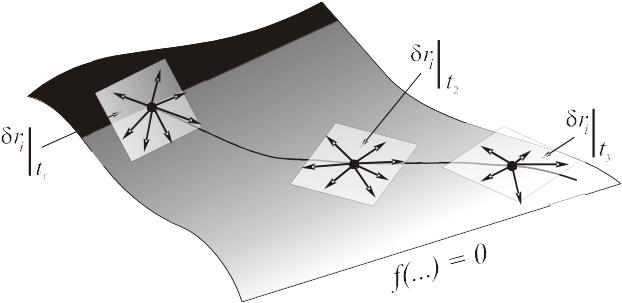
Среди множества возможных перемещений существуют несколько независимых друг от друга перемещений, через которые можно выразить все остальные перемещения. Это число независимых перемещений называют числом степеней свободы механической системы. Если точек в системе N, а на систему наложено m связей

то число степеней свободы системы равно

2727\* MERGEFORMAT ()

На возможных перемещениях, так же как и на действительных, можно вычислять работу сил:

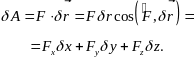2828\* MERGEFORMAT ()

Эта работа называется виртуальной работой силы.

Пусть на систему наложена геометрическая стационарная удерживающая связь

2929\* MERGEFORMAT ()

Применяя принцип освобождаемости от связей, заменим действие связи на точки системы реакцией и вычислим виртуальную работу этой реакции: .

Для различных связей вида (29) возможны следующие значения этой работы:

3030\* MERGEFORMAT ()

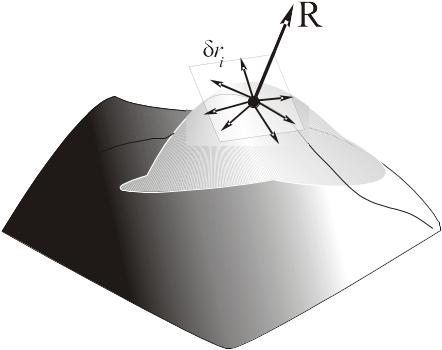
В первом случае (30) связь называется идеальной, а во втором – неидеальной.

Связь будет идеальной, если виртуальная работа реакции связи на любых возможных перемещениях равна нулю.

Неидеальными являются связи с трением.

Если на систему наложено насколько идеальных связей, то тогда

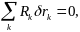3131\* MERGEFORMAT ()

где реакция k-той отброшенной связи.