Практическая часть

1. Изучить устройство, принцип действия спектрофотометра СФ– 46.

2. Зарегистрировать спектр пропускания тонкой плёнки SiO₂ на подложке NaCl, KBr в области 400– 1000 нм.

3. Проанализировать полученную спектрограмму, определить экспериментальные значения T'_max, T'_min, ν_n+1, ν_n, занести их в таблицу, составленную по форме.

T'max

T'min

νn+1

νn

Tmax

Tmin

c

n2

τ

t

x

4. По известным значениям n₃ и n₄ рассчитать по формуле (13) значения R₃ и, используя его определить по формулам (12), (16) величины T"_max, T"_min и в соответствии с (11’) и (15’) – значения T_max и T_min. Внести значения T_max и T_min в таблицу.

5. Рассчитать контрастность с по формуле (15): и затем – значение n₂, воспользовавшись формулой (17).

6. Рассчитать R₁ и R₂ по формулам (10), воспользовавшись результатами расчетов, определить значение τ по формулам (18) и(19).

7. Рассчитать: на основе формуле (14) – значение t, на основе формул (7), (8) – значения r и x.

8. Определить, пользуясь формулой (20), начиная с каких значений x, погрешность значений R₁', превышает 0,01.

9. Повторить расчёт n₂, τ, t, x для 3-4 пар экстремумов n₂(ν), x (ν). Изобразите графически зависимости n₂(ν), x (ν).

Контрольные вопросы

1. Определение оптических свойств тонких плёнок. Эллипсометрия.

2. Сущность метода Крамерса - Кронича.

3. Определения оптических постоянных тонких поглощающих плёнок по измеренным значениям коэффициентам пропускания и отражения.

4. Расчёт оптических констант прозрачных тонких плёнок по спектральной интерференционной кривой пропускания.

Литература

1. Черёмухин Г.С. Расчёт оптических характеристик плёнок “ОМП”, 1976, №6 с. 13-15.

2. Новое в исследовании поверхности твёрдого тела. Под ред. Т. Джайядевайя, Р. Ванселов. М “Мир”, 1977, 372 с.

Лабораторная работа № 3 Прочностные и энергетические характеристики металлических пленок, полученных при различных технологических режимах

Цель работы: Изучение способов измерения и методики опреде­ления прочностных и энергетических характеристик адгезии метал­лических пленок, полученных резистивным, электронно-лучевым и лазерным методом.

Приборы и принадлежности: Установка УВН-73П-2, подложки из стекла К8, кварца С5-1, металлы Al,Cu,Ni,Mo, установка для определения адгезионной прочности и прочности пок­рытий на истирание, набор зондов шириной 1мм; 1,5 мм; 2,0 мм.

Теоретическое введение

Интерес к изучению механических свойств тонких пленок (адгезия, напряжения, упругость, прочность) неуклонно возрастает, поскольку эти свойства определяют впоследствии многие эксплуатационные параметры тонкопленочных элементов.

Практически все пленки, независимо от способа их формирова­ние, находятся в состоянии внутреннего напряжения. Напряжения могут быть сжимающими (пленка стремится расшириться параллельно поверхности подложки) и растягивающими (пленка стремится сжать­ся). Для нормальных температур осаждения (от пятидесяти до нескольких сотен °С) типичные величины растягивающих напряжений в металлических пленках составляют 10⁸  10¹⁰ дин/см². Причем для тугоплавких металлов величины близки к верхнему, а для мягких – к нижнему пределу. Для диэлектрических пленок напряжение часто оказываются сжимаемыми и имеют несколько меньшие значения.

Если коэффициенты термического расширения пленки и ее подложки различны, то нагревание или охлаждение вызывают дополни­тельные напряжения в пленке, называемое термическим. При наличии внешних механических нагрузок в пленке также возникает дополнительное напряжение, называемое внешним. Общее напряжение в плёнке, таким образом, определяется суммой всех перечисленных:

С помощью технологических способов общее напряжение может быть сведено к минимуму. Внутреннее напряжение в большинстве систем является доминирующим и поэтому является предметом более пристального изучения.

Если пленка в напряженном состоянии осаждена на тонкую под­ложку, то подложка вместе с пленкой изгибается. Этот изгиб явля­ется мерой внутренних напряжений в пленке и может быть измерен. На этом принципе основаны наиболее общие методы измерения нап­ряжений.

1. Дисковый метод основан на измерении прогиба центра круг­лой пластинки после осаждения на нее пленки на одну из ее сторон. Для измерения прогиба диска используются интерференционные поло­сы, возникающие в слое между диском и оптически плоской поверх­ностью. Зная прогиб диска δ на расстоянии r от его центра, напряжение σ можно записать в следующем виде:

где E_s – модуль Юнга материала подложки;

ν – коэффициент Пуассона для материала подложки;

d_s – толщина подложки;

d_f – толщина плёнки.

Используя пластины диаметром ≈2,5 см и толщиной 2 мм можно определить напряжения от 10⁹ до 10¹¹ дин/см².

2. Метод изгибания стержня. При использовании этого метода подложку выбирают длиной в 3-5 раз больше ее ширины. Кривизну этого стержня, возникшую за счет внутренних напряжений в нанесен­ной на него пленке, находят, измеряя отклонение одного из его концов, в то время как другой конец закреплен или по изгибу се­редины стержня, если закреплены оба его конца. Регистрация изги­ба может осуществляться одним из способов; по изменению емкости; по изменению индуктивности; по току, пропущенному через нагретую проволоку; с помощью интерферометра Майкельсона и др. Если модуль Юнга пленки и подложки одинаковы, напряжение в пленке σ рассчи­тывается по измеренному радиусу кривизну стержня ρ следующим образом:

Чувствительность метода составляет ≈10⁶ дин/см².

Наряду с методами, основанными на измерении деформации пленки, возникают за счет внутренних напряжений, существует группа методов рентгеновской и электронной дифракции. Рентгеновский метод можно использовать для определения изменений параметров кристаллической решетки, а следовательно и напряжений в пленке. Метод применим, когда размеры кристаллитов пленки превышают 100 нм, в противном случае наблюдается уширение дифракционных ли­ний. Метод электронной дифракции можно применять, не ощущая эф­фекта уширения линий, до величины кристаллов, превышающих 10 нм.

Характеристики упругости тонких пленок исследовались раз­личными методами: методом измерения микроупругости, методом взду­тия, методом центрифугирования, рентгеновским и электронно-дифрак­ционным методом и др. Основная особенность, найденная при иссле­довании характеристик упругости пленок, заключается в том, что пленки оказываются прочнее, чем объемный материал.

Измерения зависимости возникающих в пленке напряжений σ от величины ее деформации Δl/l, пример которой приведен на рис.1, показывают, что начальные напряжения приводят к необратимым изме­нениям внутренних свойств плёнки. Если пленку нагрузить выше пре­дела упругости, появляется пластическая деформация (см. рис.2).

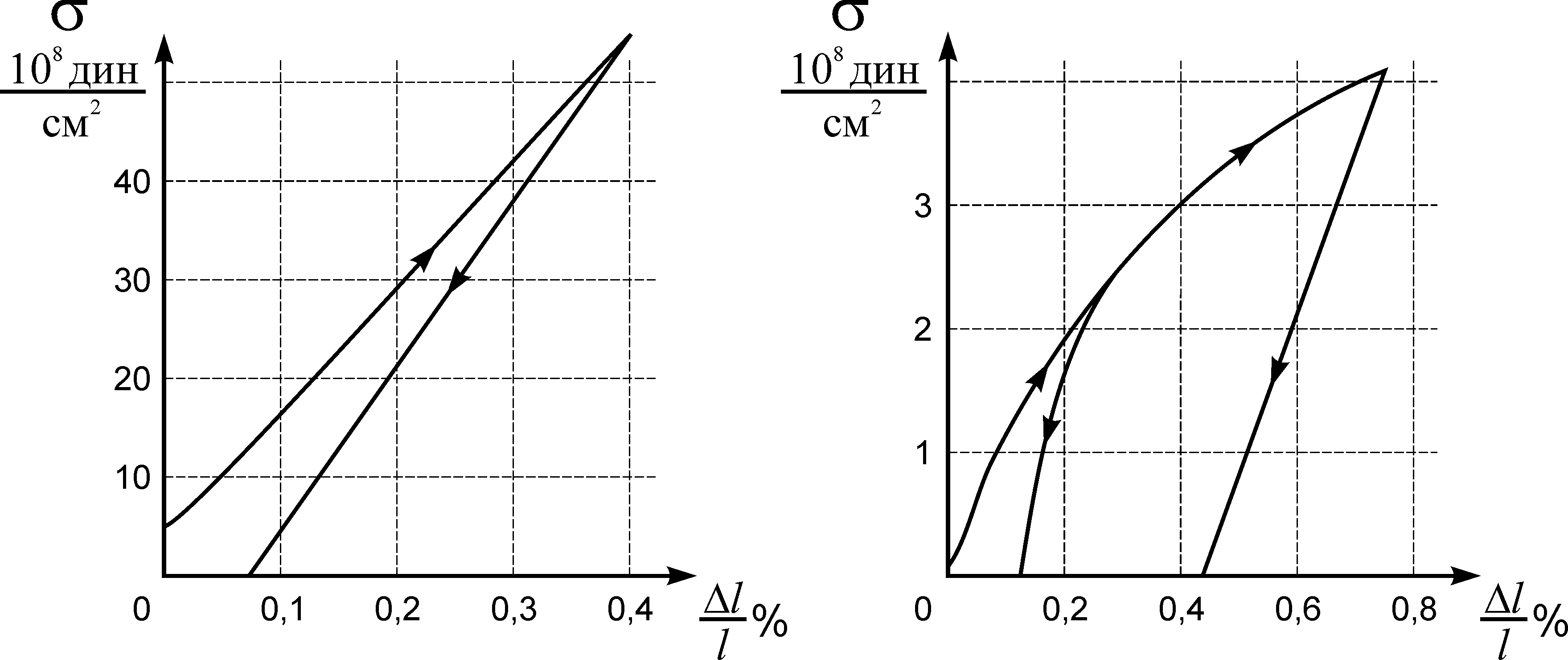
Рис.1 – Зависимость напряжений от деформации в области упругих деформаций пленок

Рис.2 – Зависимость напряжений от деформации в области плас­тических деформаций пленок золота

Установлено, что прочность, т.е. минимальные напряжения, при которых происходит разрушение пленок, примерно в 200 раз превышает прочность объемного материала. На рис.3 показана типичная кривая зависимости прочности пленки никеля от ее толщины.

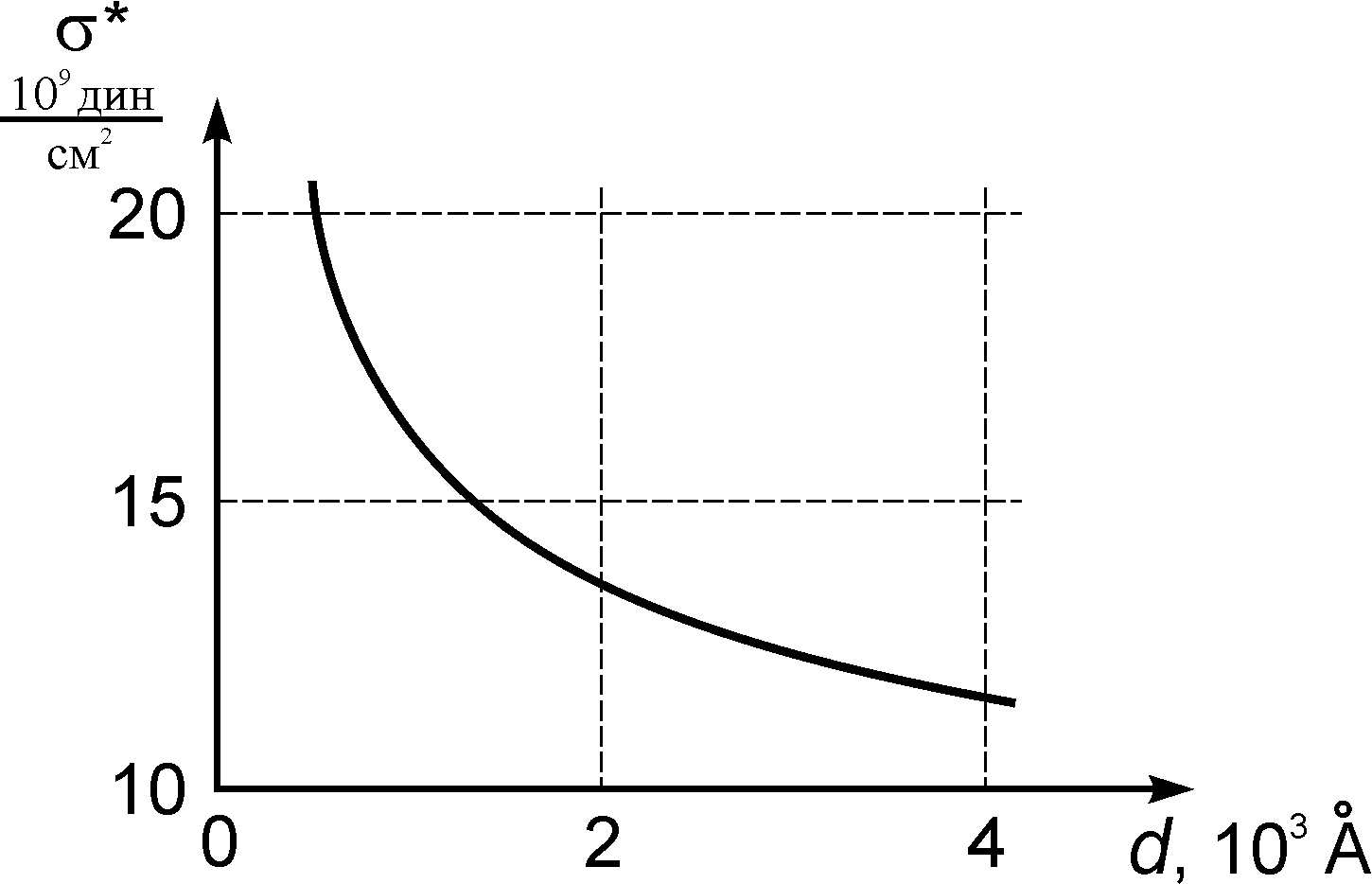
Рис. 3 – Зависимость предела прочности от толщины никелевой пленки

Из рис.3 видно, что прочность возрастает с увеличением роли поверхности. Результаты проведенных экспериментальных исследований показали, что предел прочности пленки σ^* складывается из трех составляющих:

где σ_об – величина, обусловленная внутренним строением вещества (идентичная объемному образцу);

σ_нес – величина, обусловленная наличием несовершенств струк­туры - структурными дефектами;

σ_d – величина, обусловленная наличием поверхности и зависящая от толщины пленки.

В целом зависимость предела прочности от толщины пленки мож­но представить б виде:

где К - постоянная.

Важнейшей характеристикой механических свойств пленок явля­ется адгезия.

Экспериментальные исследования показали, что значения энергии адгезионного сцепления между пленкой и подложкой варьируются от десятых долей до нескольких десятков электрон-вольт. Такой широкий диапазон энергий адгезионного сцепления может быть объяс­нен различной природой сил адгезионного сцепления в различных парах пленка-подложка: физической и химической адсорбцией.

Природа физической сорбции рассматривалась в нескольких ас­пектах. В соответствии с предположением Кизома между атомами плен­ки и подложки возникают потенциальные силы притяжения, если на поверхности подложки присутствуют постоянные диполи. Дебай предпо­ложил, что дипольные моменты могут индуцироваться в молекуле на поверхности подложки приходящим диполем. Однако эти теории не­применимы, если имеет место адсорбция неполярных молекул. В соответствии с теорией Лондона в любом атоме каждый электрон вместе с ядром образует электрический диполь, вследствие чего вращающие­ся диполи соседних атомов взаимодействуют между собой. Показано, что энергия адсорбции E_a атома конденсата и атома поверхности может быть выражена формулой:

где ₁ и ₂ – поляризуемость двух атомов;

₁ и ₂ – характеристические частоты колебаний атомов;

h – постоянная Планка;

S – равновесное расстояние между атомами конденсата и поверх­ности.

Взаимодействие между адсорбированным атомом и всей подлож­кой тогда выразится:

где N – число атомов адсорбента на единицу объема подложки;

U₁, U₂ – потенциалы ионизации взаимодействующих атомов.

Химическая природа сил адгезионного сцепления имеет место, если конденсация атомов включает химическую связь. В этом случае силы адгезионного сцепления значительно выше.

Экспериментальное измерение сил адгезионного сцепления может

осуществляться одним из перечисленных ниже методов: