Кисляков Н.И. Теория вероятности Л12 стр. 5 09.03.25

Лекция 12

12.1. Вероятность попадания нормальной случайной величины в заданный интервал

Уже известно, что если случайная величина X задана плотностью распределения f(x), то вероятность того, что X примет значение, принадлежащее интервалу (а, b), такова:

Пусть случайная величина X распределена по нор­мальному закону. Тогда вероятность того, что X примет значение, принадлежащее интервалу (a,b), равна

Преобразуем эту формулу так, чтобы можно было пользоваться готовыми таблицами. Введем новую пере­менную z = (x - a)/ . Отсюда x = z - a, dx = dz. Найдем новые пределы интегрирования. Если x = , то = ( - а)/ ; если x = , то = ( - a)/ .

Таким образом

где - функция Лапласа. Итак

(12.1)

Функция Лапласа нечетная функция: Ф(-x) = - Ф(x).

Пример. Случайная величина X распределена по нормальному закону. Математическое ожидание и среднее квадратическое откло­нение этой величины соответственно равны 30 и 12. Найти вероят­ность того, что X примет значение, принадлежащее интервалу (10, 50).

Решение. Воспользуемся формулой (52.2). По условию, =10, = 50, a =30, =10, следовательно,

По таблице находим Ф(2) = 0,4772. Отсюда иско­мая вероятность

Р(10 < X < 50) = 2 0,4772 = 0,9544.

12.2. Вычисление вероятности заданного отклонения

Часто требуется вычислить вероятность того, что отклонение нормально распределенной случайной вели­чины X от математического ожидания по абсолютной величине меньше заданного по­ложительного числа , т. е. требуется найти вероятность осуществления неравенства

.

Заменим это неравенство равносильным ему двойным неравенством

Тогда

12.3. Правило трех сигм

Положив . получим т. е. вероятность того, что отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонения, равна 0,9973.

Другими словами, вероятность того, что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала, а именно равна 0,0027. Это означает, что лишь в 0,27% случаев так может произойти. Такие события, исходя из принципа невозмож­ности маловероятных событий, можно считать практически невозможными. В этом и состоит сущность

правила трех сигм: если случайная величина распределена нормально, то абсолютная величина ее отклонения от математиче­ского ожидания не превосходит утроенного среднего квадратического отклонения.

На практике правило трех сигм применяют так: если распределение изучаемой случайной величины неизвестно, но условие, указанное в приведенном правиле, выпол­няется, то есть основание предполагать, что изучаемая величина распределена нормально; в противном случае она не распределена нормально.

12.4. Оценка отклонения теоретического распределения от нормального. Асимметрия и эксцесс

При изучении распределений, отличных от нормаль­ного распределения, возникает

необходимость количественно оценить это различие. С этой целью вводят специальные характери­стики, в частности асимметрию и эксцесс. Для нормаль­ного распределения эти характеристики равны нулю. Поэтому если для изучаемого распределения асимметрия и эксцесс имеют небольшие значения, то можно предпо­ложить близость этого распределения к нормальному. Наоборот, большие значения асимметрии и эксцесса ука­зывают на значительное отклонение от нормального.

Как оценить асимметрию? Можно доказать, что для симметричного распределения (график такого распреде­ления симметричен относительно прямой х = М (X)) каждый центральный момент нечетного порядка равен нулю. Для несимметричных распределений центральные моменты не­четного порядка отличны от нуля. Поэтому любой из этих моментов (кроме момента первого порядка, который равен нулю для любого распределения) может служить для оценки асимметрии; естественно выбрать простейший из них, т. е. момент третьего порядка . Однако принять этот момент для оценки асимметрии неудобно потому, что его величина зависит от единиц, в которых измеряется случайная величина. Чтобы устранить этот недостаток, делят на и таким образом получают безразмерную характеристику.

Асимметрией теоретического распределения называют отношение центрального момента третьего порядка к кубу среднего квадратического отклонения:

= /

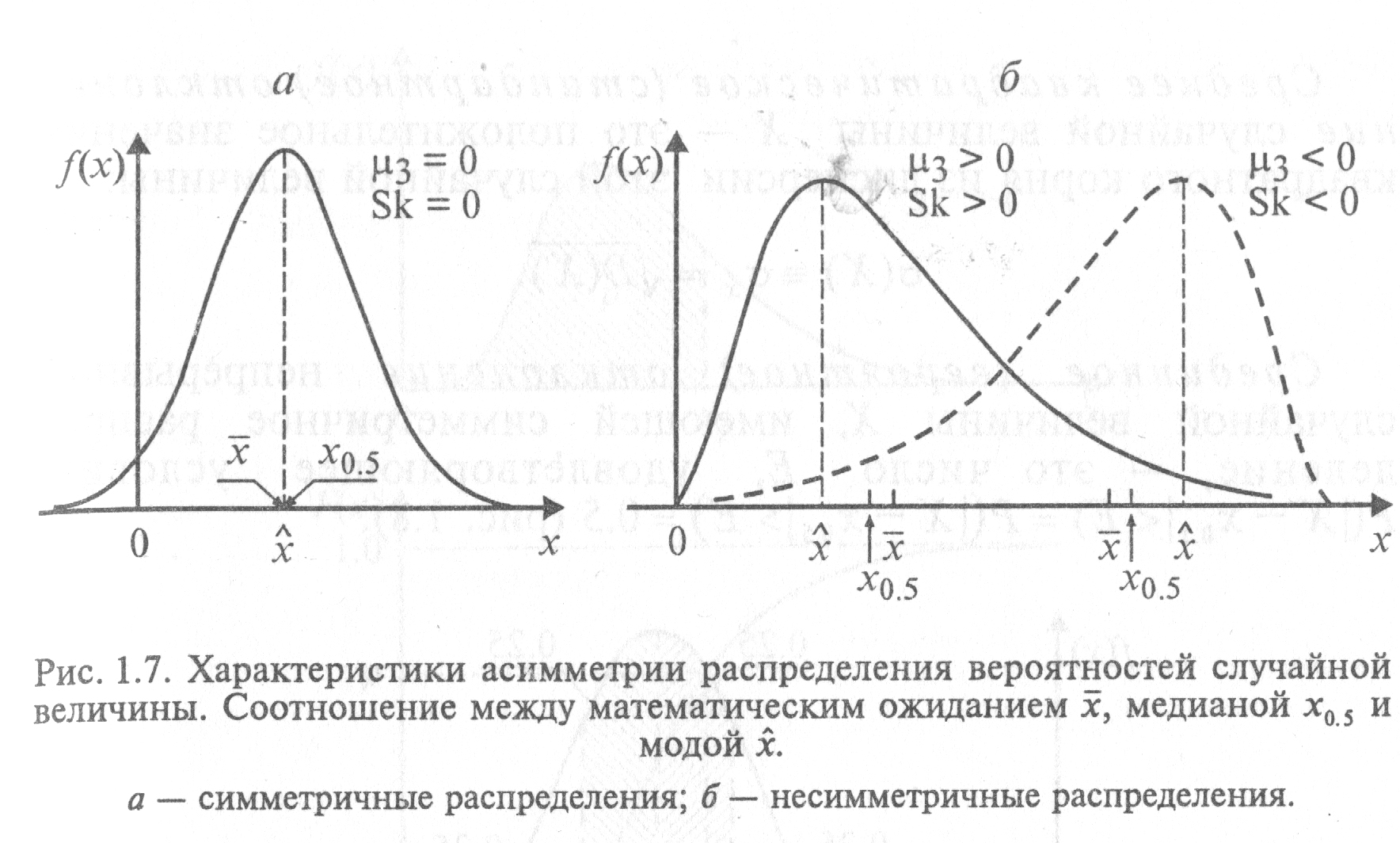
Асимметрия положительна, если «длинная часть» кри­вой распределения расположена справа от математического ожидания; асимметрия отри­цательна, если «длинная часть» кривой расположена слева от математического ожидания.

Практически оп­ределяют знак асимметрии по расположению кривой распределения относительно мо­ды (точки максимума диффе­ренциальной функции): если «длинная часть» кривой рас­положена правее моды, то асимметрия положительна, если слева - отрицательна.

Для оценки «крутости», т. е. большего или меньшего подъема кривой теоретического распределения по сравнению с нормальной кривой, пользуются характеристи­кой -

эксцессом

Эксцессом теоретического распределения называют ха­рактеристику, которая опре­деляется равенством

Для нормального распределения , следовательно, эксцесс равен нулю. Поэтому если экс­цесс некоторого распределения отличен от нуля, то кривая этого распределения отличается от нормальной кривой: если эксцесс положительный, то кривая имеет более высокую и «острую» вершину, чем нормальная кривая; если эксцесс отрицательный, то сравниваемая кривая имеет более низ­кую и «плоскую» вершину, чем нормальная кривая. При этом предполагается, что нормальное и теоретическое распределения имеют одинаковые матема­тические ожидания и дисперсии.