28. Методы наблюдения интерференции света: опыт Юнга, интерференция в тонких пленках, кольца Ньютона.

Рассмотрим подробнее интерференцию в тонких пленках.

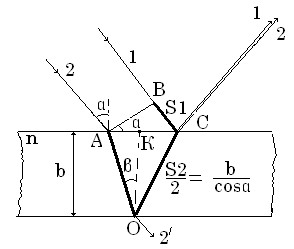
На рис. разность хода лучей 1 и 2 в точке С равна:

. (12)

Видно, что S₁ = ВС; S₂ = AO + OC;

КС = b* tgβ ; Тогда

и .

Подставим их в (12): .

Сделаем замену .

Получим .

Подставив последнее выражение в Δ, получим .

При отражении луча 1 в точке С от оптически более плотной среды фаза изменяется на π. Окончательное выражение для разности хода:

. (13)

Условия когерентности: Δ ‹ ℓ _КОГ, т.е. , Или .

Тогда . (14)

Таким образом, отраженные волны будут когерентными только при выполнении условия (14), т.е. когда удвоенная толщина пластины меньше длины когерентности.

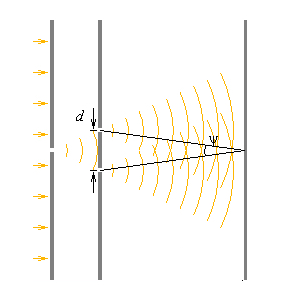
Опыт Юнга является первым интерференционным опытом, получившим объяснение на основе волновой теории. В опыте Юнга свет от источника проходит через две близко расположенные щели. Световые пучки, расширяясь из-за дифракции, падают на удаленный экран. В области перекрытия световых пучков возникают интерференционные полосы.

Если расстояние между щелями равно d, а расстояние от плоскости щелей до экрана равно L, то угол схождения лучей на экране ψ = d / L (при d << L). Угол ψ определяет ширину Δl интерференционных полос: Δl = λ / ψ = λL / d.

Измеряя ширину полос Δl, Юнг впервые определил длины волн световых лучей разного цвета.

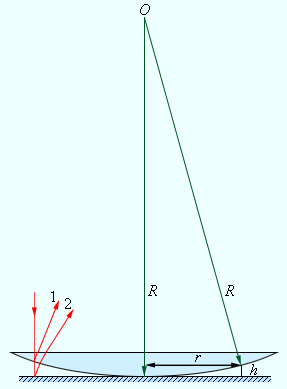
Кольца Ньютона

Интерференционная картина, возникающая при отражении света от двух поверхностей воздушного зазора между плоской стеклянной пластинкой и наложенной на нее плоско-выпуклой линзой большого радиуса кривизны, называется кольцами Ньютона. Радиусы колец Ньютона зависят от длины волны λ падающего света и радиуса кривизны R выпуклой поверхности линзы. В центре картины всегда наблюдается темное пятно. Радиус rm m-го темного кольца равен

где r1 – радиус первого темного кольца. Измеряя на опыте радиусы темных колец можно определить радиус кривизны R поверхности линзы по известному значению длины волны λ.

29.Дифракция волн. Принцип Гюйгенса-Френеля. Метод зон Френеля.

Под дифракцией понимают явления, наблюдаемые при распространении света в среде с резкими неоднородностями. В частности, наблюдается огиба­ние световыми волнами препятствий и проникновение света в область геометрической тени.

Условие дифракции: d ~ λ.

Дифракция, как и интерференция, проявляется в перераспределении светового потока при наложении когерентных волн. Различие: при интерференции рассматривается конечное число источников света, при дифракции – непрерывно расположенные.

Схема наблюдения дифракции: источник - непрозрачная преграда - экран.

Два вида дифракции: Френеля для сферических волн, Фраунгофера – для плоских.

Принцип Гюйгенса-Френеля

Принцип Гюйгенса объясняет проникновение света в область тени, но не дает сведений об амплитуде волн. Согласно принципу Г-Ф учет амплитуд и фаз вторичных волн при их интерференции позволяет найти амплитуду результирующей волны в любой точке.

От каждого участка dS волновой поверхности S в точку Р приходит колебание

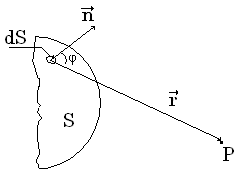
(1)

и для всей поверхности S

(2)

К(φ) = 1 при φ = 0; К(φ) = 0 при φ = π/2.

Расчет по (2) –очень сложная задача, но при определенной симметрии по методу зон Френеля определение амплитуды сильно упрощается.

Суть метода: От точечного источника S распространяется сферическая волна. Волновые поверхности симметричны относительно SP. Волновую поверхность разобъем на равные по площади кольцевые зоны так, чтобы расстояния от краев каждой зоны до т. Р отличались на λ/2. Тогда колебания в т. Р от 2-х соседних зон приходят в противофазе и, поскольку амплитуды от равных площадей волновой поверхности считаются одинаковыми (по Френелю), то при четном числе зон в т. Р будет максимум интенсивности (амплитуды), а при нечетном – максимум.

Метод зон Френеля позволил на основе волновой теории объяснить закон прямолинейного распространения света.