22. Тип записи в Паскале .

Записи - структура данных, состоящая из фиксированного числа элементов определенного типаЗапись представляет собой набор элементов разных типов, каждый из которых имеет свое имя и называется полем записи. Тип записи конструируется следующим образом:

record список полей1: тип1; ... список полейN: типN; end

type   Date=record     Day: 1..31;     Month: (Jan, Feb, Mar, Apr, May, Jun, Jul, Aug, Sep, Oct, Nov, Dec);     Year: Integer;   end;

Теперь можно объявить переменные типа Date:

var d1,d2: Date;

Чтобы получить доступ к полям записи, следует воспользоваться точечной нотацией, указав имя переменной-записи и поле, разделенные точкой:

d1.Day:=9; d1.Month:=Sep; d1.Year:=2004;

Как и для массивов, можно скопировать содержимое полей одной переменной-записи в другую:

d2:=d1;

23.Булева алгебра

Булева алгебра. Операции отрицания, логического сложения и логического умножения.

Алгебра логики — раздел математической логики, в котором изучаются логические операции над высказываниями. Высказывания могут быть истинными и ложными.

Аксиомы

1. x=x, x=x; 2. x*x=0;

3. x+1=1; 4. x+x=x, x=x+x+x;

5. x+0=x; 6. x*x=x, x=x*x*x;

7. x*0=0; 8. x*1=x;

9. x+x=1. 10. x+y=x*y

11. x*y=x+y

Упрощение логических формул. Законы.

1.переместительный x+y=y+x; xy=yx

2.сочетательный (x+y)+z=x+(y+z)

3.распределительный (x+y)z=xz+yz

булева алгебра- boolean algebra - алгебраическая структура с тремя операциями И, ИЛИ, НЕ.

Данная алгебра так названа в честь ирландца Джона Буля, который ввел ее, изучая законы логики. Булева алгебра оперирует с переменными, которые принимают два значения: "истина"= логическая единица 1, либо "ложь"= логический ноль 0. Над этими переменными выполняются операции вида:

конъюнкция (И - &, *), именуемая также логическим умножением, и определяемая равенствами: 0х0 = 0, 0х1 = 0, 1х0.= 0, 1х1 = 1.

дизъюнкция (ИЛИ - +, V), называемая также логическим сложением, и характеризуемая равенствами: 0+0=0, 0+1=1, 1+0=1, 1+1=1;

отрицанием (НЕ – черта сверху), определяемым равенствами: не 0=1, не1=0.

Операции И, ИЛИ, НЕ реализуются логическими элементами, которые являются компонентами Интегральной Схемы (ИС). Элемент выполняет одну из трех указанных выше операций либо комбинацию из этих логических операций. Например, двух операций, НЕ-И. В список логических элементов включают также триггеры и счетчики, каждый из которых выполняет более сложные логические преобразования.

На булеву алгебру опираются алгебры высказываний. Здесь на основе логических операций (связок) И, ИЛИ, НЕ строятся сложные высказывания, определяющие логические выводы. Язык булевой алгебры очень удобен для описания функционирования устройств, решающих логические задачи.

24.Правила записи логической формулы по таблице счисления

Простейшая таблица истинности – на выходе одна единица и все нули, один ноль и все единицы. Получение логических формул для простейших таблиц: 1.Имеем один логический ноль на выходе

X Y Q

0 0 1 Q=f(X,Y)

0 1 0 Ответ: Q=X+Y

1 0 1

1 1 1

С помощью операции логического сложения записываем выражение, соответствующее этому нулю. 2.Имеем одну логическую единицу на выходе

X Y Q

0 0 0

0 1 1 Ответ: Q=XY

1 0 0

1 1 0

С помощью операции логического умножения записываем выражение, соответствующее единице.

Получение логической формулы для любых таблиц:

1.По единицам:Для каждой единице на выходе записываем логическую формулу, как это делалось в случае простейшей таблицы. Общий результат равен логической сумме этих выражений.

X Y Q

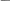0 1 0 Q₃=XY Q₄=XY

1 0 0

0 0 1 Ответ: Q=XY+XY

1 1 1

2.По нулям:Для каждого нуля на выходе таблицы записываем выражение также, как делалось для простейшее таблицы истинности. Общее выражение равно логическому произведению этих выражений.

X Y Q

0 0 0 Q₁=X+Y Q₃=X+Y

0 1 1

1 0 0 Ответ: Q=(X+Y)(X+Y)

1 1 1