Выражение (5.23) имеет два полюса

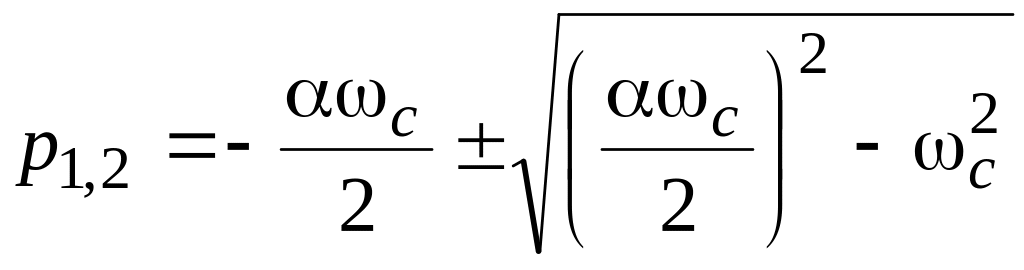, (5.24)

откуда следует, что при  < 2 полюсы коэффициента передачи будут комплексно-сопряженными, а при  > 2  вещественными. Амплитудно-частотные характеристики ФНЧ второго порядка для различных значений  < 2 приведены на рис. 5.11, а.

При   0 добротность Q  . При этом фильтр будет возбуждаться на частоте _с. Практическая реализация ФНЧ второго порядка возможна при использовании в качестве четырехполюсников А и В звеньев д и ж из табл. 5.1. Схема такого фильтра приведена на рис. 5.11, б.

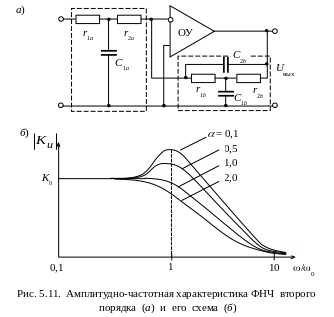
В соответствии с табл. 5.1 частота среза этого фильтра определяется выражением

,

добротность фильтра 

,

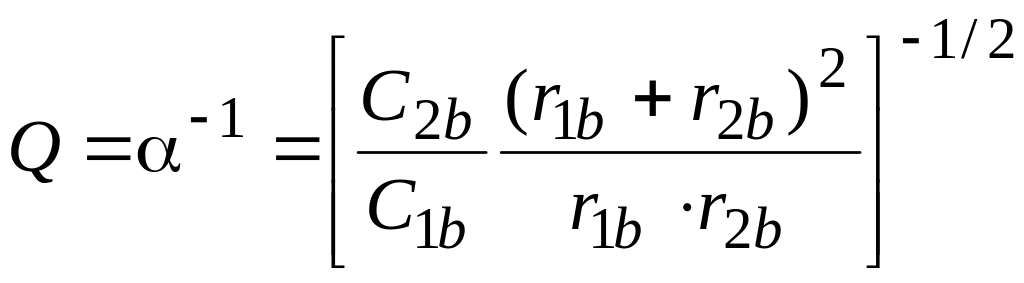а коэффициент передачи на постоянном напряжении 

.

Б. Фильтр верхних частот (ФВЧ) с одноконтурной обратной связью

Этот фильтр предназна­чен для выделения сигналов, частота которых выше некоторой заданной частоты, называемой частотой среза фильтра. ФВЧ практически без ослабления пропускает сигналы выше частоты среза и ослабляет сигналы с частотой ниже частоты среза. В зависимости от числа полюсов в передаточной характеристике ФВЧ делят на однополюсные (первого порядка) и двухполюсные (второго порядка). Схема ФВЧ первого порядка приведена на рис. 5.12, а. В этой схеме изменен только четы­рехполюсник А, в котором сопротивление r_а заменено емкостью С_а. Передаточные проводимости пассивных четырехполюсников имеют значения:

; .

Коэффициент передачи фильтра определяется по формуле (5.20) и равен

, , (5.25)

где K₀ = C_a /C_b  коэффициент передачи фильтра на бесконечно высокой частоте, а _c = (r_bC_b) '  частота среза фильтра.

Амплитудно-частотная характеристика ФВЧ первого порядка приведена на рис. 5.12, б. На частоте среза фильтра коэффициент передачи фильтра достигает значения 0,707К₀.

Передаточная характеристика ФВЧ второго порядка определяется в общем случае выражением

, (5.26)

которое имеет два полюса

.

Амплитудно-частотная характеристика такого фильтра определяется формулой

(5.27)

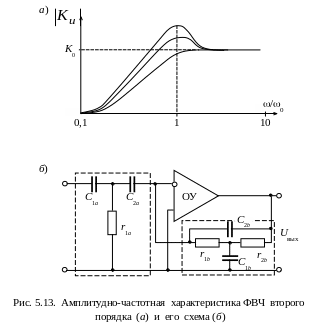
и имеет вид, изображенный на рис. 5.13, а.

При значении  < 2 полюсы коэффициента передачи ФВЧ являются комплексно сопряженными, а при  > 2 – вещественными. Для получения максимально гладкой характеристики ФВЧ обычно выбирают   . При этом наклон характеристики составляет 40 дБ на декаду.

Практическая схема ФВЧ второго порядка приведена на рис. 5.13 б. Она по­лучена при использовании в качестве четырехполюсников А и В звеньев е и ж, приведенных в табл. 5.1.

В соответствии с характеристиками звеньев фильтра основные характеристики ФВЧ определяются выражениями:

 частота среза фильтра:

;

 коэффициент передачи на высокой частоте

; (5.28)

 добротность:

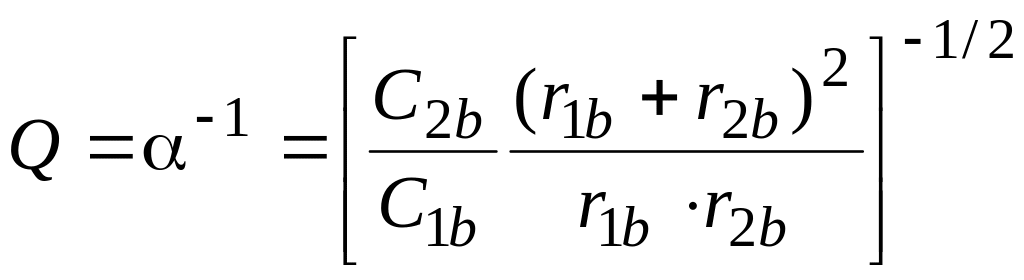. (5.29)

В. Полосовой фильтр с одноконтурной обратной связью (ПФ)

Данный фильтр предназначен для выделения сигналов, частота которых лежит в пределах некоторой полосы . При этом он практически без ослабления пропускает сигналы, лежа­щие в этой полосе, и ослабляет сигналы, частоты которых лежат за пределами полосы пропускания. Полосовые фильтры бывают двухполюсные (второго порядка) и многополюс­ные (высокого порядка). Передаточная характеристика ПФ второго порядка оп­ределяется выражением

, (5.30)

которое имеет два комплексно сопряженных полюса  ₀₁ и ₀₂. Затухание фильтра и его добротность имеют значения

, ,

где .

Максимальное усиление ПФ в полосе пропускания равно К₀ на частоте  = ₀. Комплексная амплитудно-частотная характеристика ПФ определяется выражением

, (5.31)

откуда получаем значение ее модуля

. (5.32)

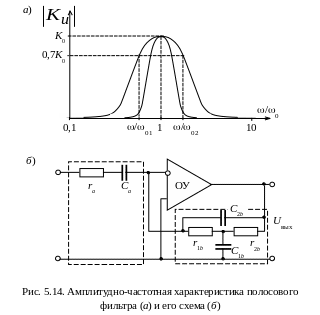
График амплитудно-частотной характеристики полосового фильтра для двух значений доб­ротности приведен на рис. 5.14, а.

С повышением добротности полоса пропуска­ния такого фильтра сужается, при этом максимальное усиление на частоте  = ₀ остается неизменным. Реализовать полосовой фильтр можно при использовании в качестве четырехполюсников А и В звеньев г и ж из табл. 5.1. Схема такого полосового фильтра приведена на рис. 5.14, б.

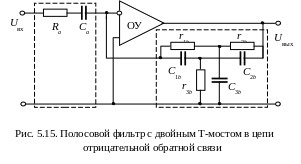
Аналогичные результаты можно получить, если использовать в качестве четырехполюсников А и Б звенья г и и из табл. 5.1. Схема полосового фильтра, у которого в цепи отрицательной обратной связи включен двойной Т-мост, а на входе  последовательно включенные сопротивление и емкость, приведена на рис. 5.15.

Г. Заграждающий фильтр с одноконтурной обратной связью

Этот фильтр имеет частотную характеристику, противоположную частотной характеристике узкополосного фильтра. Заграждающий фильтр (ЗФ) ослабляет сигналы в полосе частот ₀₁ <  < ₀₂ и пропускает на выход сигналы, частота которых лежит за пределами этой полосы частот. Передаточную функцию ЗФ можно получить, используя передаточную функцию ПФ:

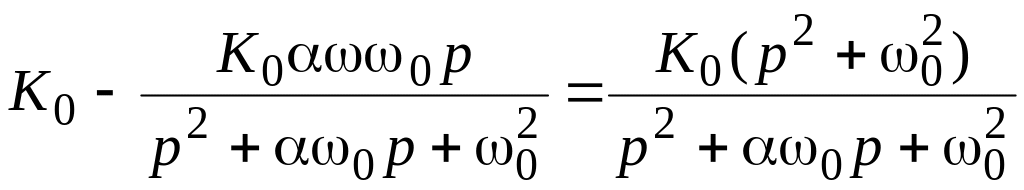= , (5.33)

где К₀  коэффициент передачи ЗФ на постоянном напряжении.

Комплексная амплитудно-частотная характеристика ЗФ в соответствии с выражением (6.33) имеет вид

, (5.34)

откуда получаем значение ее модуля

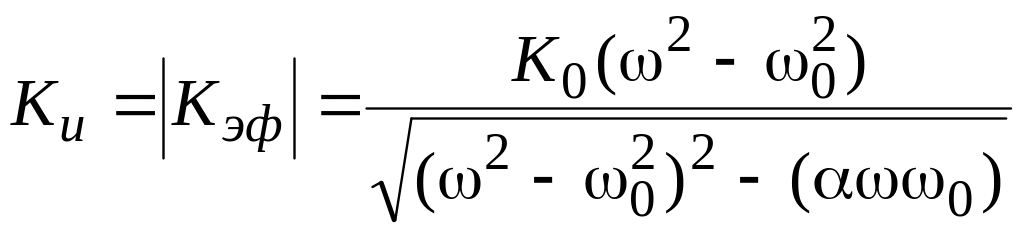. (5.35)

Амплитудно-частотная характеристика ЗФ изображена на рис. 5.16, а. На частоте  = ₀ имеет К_u, а на постоянном напряжении ( = 0) получаем К_u = К₀. С повышением частоты К_эф также стремится к значению К_u = К₀.

Реализовать ЗФ с такой характеристикой можно при использовании в качестве четырехполюсников А и В звеньев и и ж из табл. 2.1. Схема ЗФ с этими звеньями приведена на рис. 5.16. Для этой схемы можно получить уравнение вида (5.34), если положить, что _1а = _2а = _2b = , т.е. выполнить условия

,

,

.

При этом получим, что

; ,

т.е. характеристики К₀ и ₀ такие же, как у ФНЧ второго порядка.