1. Пример анализа алгоритмов

Задание

Оцените эффективность двух приведенных ниже алгоритмов сортировки

Сортировка вставками

INSERTION-SORT (A) стоимость число раз

1 for j ← 2 to length [A] с1

2 do key ← A[j] с2

3 // добавить A[j] к отсортированной части A[1..j-1] с3=0

4 i ← j – 1 с4

5 while i > 0 and A[i] > key с5

6 do A[i + 1] ← A[i ] с6

7 i ← i – 1 с7

8 A[i + 1] ← key с8

Сортировка слиянием

MERGE-SORT (A, p, r)

1 if p < r

2 then q ← | (p + r) /2 |

3 MERGE-SORT(A, p, q )

4 MERGE-SORT(A, q + 1, r )

5 MERGE(A, p, q, r )

Вспомогательная процедура MERGE(A, p, q, r ) соединяет два упорядоченных массива в один. Параметрами этой процедуры являются массив А и числа p, q, r, указывающие границы сливаемых участков. Процедура предполагает, что p ≤ q < r и что участки A[p..q} и A[q+1..r] уже отсортированы, и сливает их в один участок A[p..r]

Время работы процедуры MeRGE есть Θ (n ), где n – общая длина сливаемых участков (n= r – p +1)

4. Выполнение операторов программы

Вычисление выражений

Приоритет операций:

↑ (возведение в степень)

+, - (знак)

*, / (умножение, деление)

+, - (сложение, вычитание)

<, >, =, ≤, ≥, ≠ (операции отношения)

not (записывается также в виде )

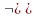and (записывается также в виде )

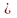or (записывается также в виде )

(логическая импликация)

Пример. Массив Y описан для значений индекса только от 1 до 10.

Значения переменных n = 11, х = 3

Пусть требуется вычислить значение выражения (n ≤ 10 and Y[n]=x )

11 ≤ 10 and Y[11]=3

ложно and (не определено = 3)

ложно and не определено

ложно

Выполнение оператора присваивания

x := E(x, y,…)

Аксиома

х′- значение переменной x до выполнения оператора присваивания

х′′- значение переменной x после выполнения оператора присваивания

x′′ = E(x′, y′,…)

y′′ = y′

1. Основы доказательства корректности

Формулируется математическая теорема о результатах выполнения сегмента программы:

Если условие V (предусловие) истинно непосредственно перед выполнением сегмента программы, тогда после выполнения сегмента тоже истнинно будет условие P (постусловие)

{V} S {P}

V есть предусловие для постусловия P по отношению к оператору S

Оператор частично корректный, если выполнение оператора приводит к получению правильного результата, когда бы он ни завершился.

Оператор полностью корректный, если для частично корректного оператора доказано, что его выполнение действительно заканчивается.

2. Правила вывода

1. Правило вывода Р1 – усиление предусловия и ослабление постусловия

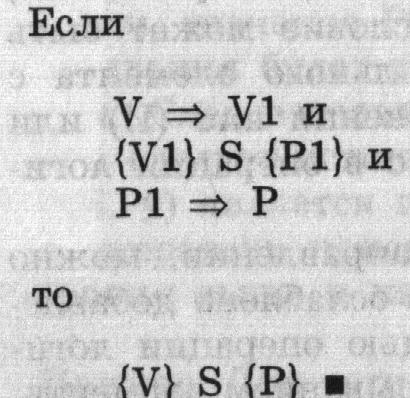
2. Правило вывода А1 – получение предусловия оператора присваивания

{?} x:=E {P}

V = P^x_E

Чтобы получить предусловие для заданного постусловия Р по отношению к заданному оператору присваивания x:=E , подставим выражение (Е) вместо переменной с именем х всюду, где это имя встечается в постусловии Р.

Правило вывода А2 – Проверка предусловия оператора присваивания

{V} x:=E {P}

Если

То

{V} x:=E {P}

3. Правило вывода IF1 - Проверка предусловия условного оператора

Если

{V and B} S1 {P} и

{V and not B} S2 {P}

то

{V} if B then S1 else S2 endif {P}

4. Правило вывода IF2 – Получение предусловия условного оператора

Если

{V1} S1 {P} и

{V2} S2 {P}

то

{(V1 and B) or (V2 and not B)} if B then S1 else S2 endif {P}

5. Правило вывода IF3 –Условный оператор

Если

{V1} S1 {P} и

{V2} S2 {P}

то

{V1 and V2 }if B then S1 else S2 endif {P}

6. Правило вывода IF4 – Условный оператор

Если

{V1 and B} S1 {P} и

{V2 and not B} S2 {P}

то

{V1 and V2 }if B then S1 else S2 endif {P}

7. Правило вывода S1 – Последовательность операторов

Если

{V} S1 {P1} и

{P1} S2 {P}

то

{V} (S1; S2) {P}

8. Правило вывода W1 – Цикл с условием продолжения без инициализации

Если

{I and B} S {I}

то

{I} while B do S endwhile {I and not B)

Условие I называют инвариантом цикла.

9. Правило вывода W2 – Цикл с условием продолжения с инициализацией

Пусть задано условие I (инвариант цикла)

Если

{V} инициализация {I} и

{I and B} S {I} и

{I and not B} P

то

{V} (инициализация; while B do S endwhile ){P}

Чтобы доказать частичную корректность цикла с условием продолжения с помощью праила вывода W2, необходимо:

1. найти инвариант цикла I,

2. доказать, что {V} инициализация {I},

3.доказать, что {I and B} S {I},

4. доказать, что {I and not B} P

Для доказательства, что цикл полностью корректный необходимо дополнительно показать, что цикл завершается.

10. Правило вывода DC1 – разделяй и властвуй

Если

{V1} S{P1} и

{V2} S {P2}

то

{V1 and V2 } S { P1 and P2 }

11. Правило вывода DC2 – разделяй и властвуй

Если

{V1} S{P1} и

{V2} S {P2}

то

{V1 orV2 } S { P1 or P2 }

12. Правило вывода DC3 – разделяй и властвуй

Если

{V} S{P1} и

{V} S {P2}

то

{V } S { P1 and P2 }

13. Правило вывода DC4 – разделяй и властвуй

Если

{V} S{P1} и

{V} S {P2}

то

{V } S { P1 or P2 }

5. Инвариант цикла

Цикл с условием продолжения без инициализации

Если

{I and B} S {I}

то

{I} while B do S endwhile {I and not B)

Условие I называют инвариантом цикла.

Численный алгоритм

Программа

a:=x; b:=y; c:=0;

while b ≠ 0 do

{}

{} b:=b-1; c:=c+a

end

{}

Для данной программы определите, что является аргументом и что является результатом.

Произведите прокрутку алгоритма для значений х=7 и у = 13, заполняя таблицу

Операция	Расчет	Инвариант цикла	Пароль
a:=7; b:=13; c:=0	a=7; b=13; c=0		b≠0
b:=b-1; c:=c+a	a=7; b=12; c=7		b≠0
b:=b-1; c:=c+a	a=7; b=11; c=14		b≠0
			b=0

Запишите выражение для инварианта цикла

Программа – алгоритм 1

a:=x; b:=y; c:=0;

while b ≠ 0 do

{высказывание: a*b+c=x*y}

{высказывание: b≠0} b:=b-1; c:=c+a

end

{ высказывание: a*b+c=x*y и b = 0 дает с = x*y}

Инвариант цикла

I = a*b+c=x*y

Алгоритм 1 – программа перемножения двух натуральных чисел с использованием метода повторных сложений.

Усовершенствованный алгоритм перемножения натуральных чисел

Программа – алгоритм 2

a:=x; b:=y; c:=0;

while b ≠ 0 do

{высказывание: a*b+c=x*y}

{высказывание: b≠0} c:=c+a* (b MOD 10);

a:= a*10;

b:=b DIV 10

end

{ высказывание: a*b+c=x*y и b = 0 дает с = x*y}

Операция	Расчет	Инвариант цикла	Пароль
a:=7; b:=13; c:=0	a=7; b=13; c=0	7*13+0=7*13	b≠0
c:=c+a* (b MOD 10); a:= a*10; b:=b DIV 10	c=0+7* (13 MOD 10)= a= 7*10= b=13 DIV 10 =		b≠0
			b=0

Усовершенствованный алгоритм перемножения натуральных чисел

Программа – алгоритм 3

a:=x; b:=y; c:=0;

while b ≠ 0 do

{высказывание: a*b+c=x*y}

{ высказывание: b ≠ 0 } if Odd (b) then c:=c+a;

a:= a*2;

b:=b DIV 2

end

{ высказывание: a*b+c=x*y и b = 0 дает с = x*y}

Операция	Расчет	Инвариант цикла	Пароль
a:=7; b:=13; c:=0	a=7; b=13; c=0	7*13+0=7*13	b≠0
if Odd (b) then c:=c+a a:= a*2 b:=b DIV 2	c = a= b=		b≠0
			b=0