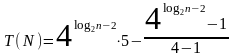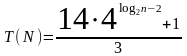Основы анализа программ
Последовательность действий алгоритма определяется входными данными
Например, алгоритм поиска наибольшего элемента в списке из N элементов
1 largest list[1]
2 for i 2 to N do
3 if (list[i] > largest) then
4 largest list[i]
Если список упорядочен в порядке убывания, одно присваивание выполняется до начала цикла, в теле цикла присваиваний не будет.
Если список упорядочен в порядке возрастания, всего будет сделано N присваиваний.
При анализе должны рассмотреть различные возможные множества входных значений.
Различные входные множества можно разбить на классы, в зависимости от поведения алгоритма на каждом множестве. Это позволяет уменьшить число рассматриваемых возможностей.
Например, число различных расстановок 10 различных чисел в списке есть 10!=3 628 800
Применим к списку из 10 чисел алгоритм поиска наибольшего элемента.
Можно выделить класс, который содержит все входные множества, у которых первое число является наибольшим (362880 входных множеств);
Можно выделить класс, который содержит все входные множества, у которых второе число является наибольшим (362880 входных множеств);
и т.д.
Классы входных данных
Необходимо анализировать работу алгоритма на различных наборах данных
Наилучший случай
Наилучшим случаем является тот набор данных на котором алгоритм выполняет меньше всего действий
Наихудший случай
При анализе наихудшего случая необходимо выбрать набор данных, на котором алгоритм выполняет больше всего работы
Средний случай
Анализ самый сложный.
В основе анализа лежит определение различных групп, на которые следует разбить возможные входные наборы .
На втором шаге определяется вероятность, с которой входной набор принадлежит каждой группе.
На третьем шаге подсчитывается время работы алгоритма на данных из каждой группы.
Среднее время работы вычисляется по формуле
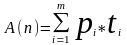
Необходимые математические сведения
Округление числа Х влево называется наибольшее целое число, не превосходящее Х.
|_ 2,5_| = 2, |_- 7,3_| = -8
Округление числа Х вправо называется наименьшее целое число, которое не меньше чем Х.
|– 2,5–| = 3, |– 7,3–| = -7
Формулы суммирования
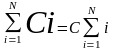
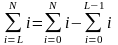
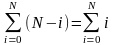
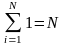
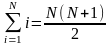
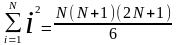
для любого числа A
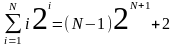
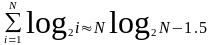
Скорости роста
Алгоритмы вида «разделяй и властвуй»
Пример алгоритма
DivideAndConquer(data,N,solution)
data
N
solution
if (N <= SizeLimit) then
DirectSolution(data,N,solution)
else
DivideInput(data,N,smallerSets, smallerSizes, numberSmaller)
for i=1 to numberSmaller do
DivideAndConquer(smallerSets[i], smallerSizes[i],smalSol[i])
end for
CombineSolutions(smallSol, numberSmaller, solution)
End if
При N<= SizeLimit
DAC(N)= DIR (N)
При N > SizeLimit
DAC(N)= DIV (N) +
)+
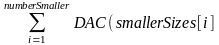COM(N)
Где
DAC – сложность алгоритма DivideAndConquer
DIR– сложность алгоритма DirectSolution
DIV– сложность алгоритма DivideInput
COM– сложность алгоритма CombineSolutions
Метод турниров
Рекуррентные соотношения
Рекуррентные соотношения на сложность алгоритма выводятся непосредственно из вида алгоритма, однако с их помощью нельзя быстро вычислить эту сложность.
Необходимо привести рекуррентные соотношения к замкнутому виду.
Метод подстановок
Последовательно производим подстановки и пытаемся уловить общий принцип.
Пример 1.
Имеем рекуррентное соотношение
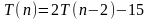
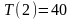
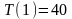
Подставим в
первое равенство эквивалентное выражение
для
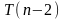
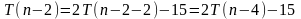
Теперь необходимо исключить значение
Выполняем последовательность подстановок
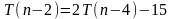
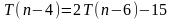
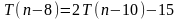
Будем подставлять результаты в исходное уравнение
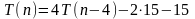
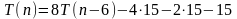
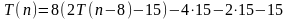
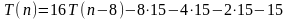
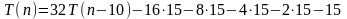
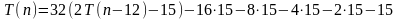
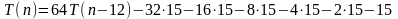
Необходимо уловить общую схему
Слагаемые с конца представляют собой число -15, умноженное на очередную степень двойки.
Коэффициент при рекурсивном вызове функции T является степенью двойки.
Аргумент функции T всякий раз уменьшается на 2.
Процесс завершится, когда мы доберемся
до значения
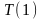или
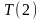
Сколько нужно сделать подстановок?
При четном
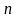нужно сделать
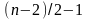подстановок.
Это даст
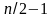слагаемых с множителем -15 и
степень двойки перед
.
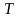Например, при
нужно сделать пять подстановок; получим
шесть слагаемых с множителем -15, и
коэффициент при
будет равен
.
Для четных значений имеем
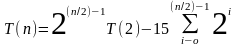
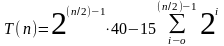
Для нечетных значений имеем
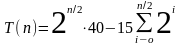
Применяя равенство
получаем для четного
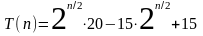
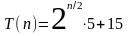
Действуя аналогично получаем для нечетного
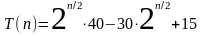
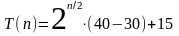
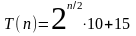
Пример 2
Имеем рекуррентное соотношение
,
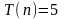если
;
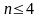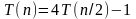в противном случае
Будем действовать так же как в предыдущем случае
Сначала будет подставлять значения для . В результате приходим к равенствам
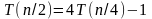
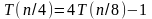
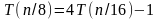
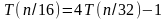
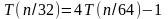
Последовательно производим подстановку этих равенств в исходное уравнение.
,
;
,
,
,
,
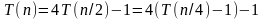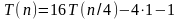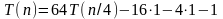
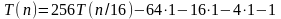
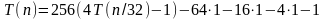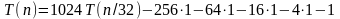
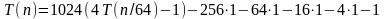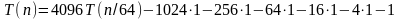
Выявляем закономерности:
коэффициент при -1 увеличивается в некоторую степень четверки раз;
степень двойки, на которую мы делим аргумент, всякий раз на 1 больше наибольшей степени четверки при -1;
степень четверки в коэффициенте при такая же, что и степень двойки, на которую мы делим аргумент.
При
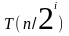этот коэффициент равен
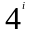
При каком значении
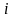подстановки
должны прекратиться?
Поскольку значения заданы явно при
можно остановиться, добравшись до
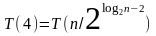
В результате получаем
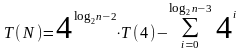
Упростим выражение используя соотношение
