12. Топологическая сортировка

Пусть имеется ориентированный граф G=(V,E) без циклов (directed acyclic graf).

Задача о топологической сортировке (topological sort) этого графа состоит в следующем: надо указать такой линейный порядок на его вершинах, что любое ребро ведет от меньшей вершины к большей (в смысле этого порядка)

Алгоритм топологической сортировки

TOPOLOGICAL-SORT (G)

1. вызвать DFS(G) , при этом

2. завершая обработку вершины

( DFS-VISIT, строка 8),

добавлять ее в начало списка

3. вернуть построенный список вершин

Топологическая сортировка выполняется за время Θ (V + E), потому что столько времени занимает поиск в глубину, а добавлять каждую из | V | вершин к списку можно за время O(1).

14. Деревья

Деревья

Рекурсивные процедуры обхода деревьев

Прямой обход

procedure PREODER (n: узел);

begin

1. Занести в список обхода узел n;

2. for для каждого сына с узла n в порядке слева направо do PREORDER (c )

end; { PREODER}

Симметричный обход

procedure INODER (n: узел);

begin

if n - лист then

занести в список обхода узел ;

else begin

INORDER (самый левый сын узла n);

занести в список обхода узел n;

for для каждого сына с узла n, исключая

самый левый, порядке слева направо do

INORDER ( c )

end

end; { INODER}

Операторы АТД, основанные на деревьях:

1.PARENT (n, T)

2. LEFTMOST_CHILD (n, T)

3. RIGHT_SIBLING (n, T)

4. LABEL (n, T)

5. CREATi (v, T₁,T₂,…T_i)

6. ROOT( T)

7. MAKENULL ( T)

1. АВЛ-деревья

1962 год

Московские математики Г.М.Адельсон-Вельский и Е.М.Ландис предложили схему самобалансирующегося поискового дерева. Для балансировки дерева требуется произвести каждый раз небольшие преобразования, которые затрагивают не более трех узлов.

Высота дерева – длина наибольшего пути в этом дереве.

Вершина дерева называется сбалансированной, если высота ее левого и правого поддерева отличается не более чем на 1.

Дерево называется подравненным, если все его вершины сбалансированы.

При добавлении в дерево новых вершин, некоторые вершины могут стать несбалансированными. Сбалансированность может пропасть только у вершин, лежащих на пути от корня дерева к новой вершине, и разность высот достигает значения 2.

Обозначим a самую нижнюю вершину с нарушенным балансом. Две следующие вершины на этом пути обозначим как b и c.

Возможные схемы взаимного расположения вершин (для нижней части дерева вниз от a) для случая, когда левый путь длиннее правого на 2, изображен на рисунке.

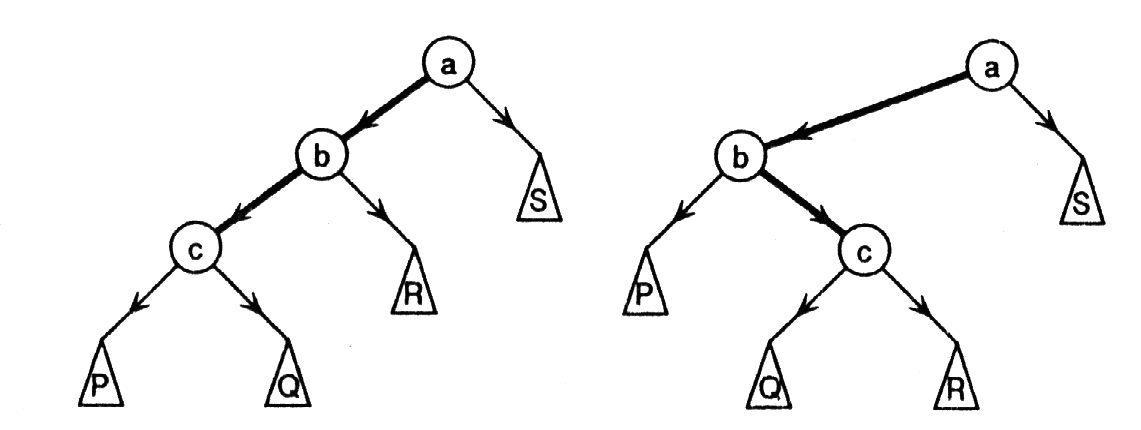
Все остальные части дерева изображены условными блоками. Достаточно небольшого изменения вершин a, b, c и прицепленных к ним деревьев, чтобы балланс восстановился во всех вершинах. Эти изменения представлены на рисунке.

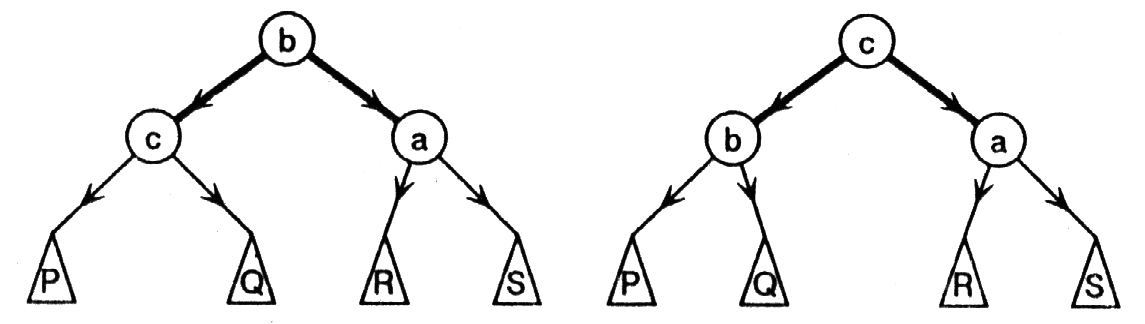
Фактически нужна только одна операция – поднятие вершины на один уровень наверх. Для первого случая нужно поднять наверх вершину b один раз, а во втором случае – вершину c два раза.

В настоящее время в некоторых схемах, где требуется быстрый доступ к часто меняющейся информации, применяется адаптирующееся дерево, основанное на АВЛ-преобразованиях.

В современных информационных системах данные хранятся преимущественно во внешней памяти, а время, расходуемое на одно обращение к диску существенно больше времени, требуемого на сопутствующие вычисления.

Поэтому целесообразно в каждом узле дерева ветвить поиск не на два варианта, а на много.

В информационных системах АВЛ деревья уступили место более прогрессивной конструкции В-дерева и различным его обобщениям.

Различные классы балансирующихся двоичных деревьев и В-деревьев рассмотрены в книге Т.Кормен, Ч.Лейзерсон, З. Ривест Алгоритмы: построение и анализ. М.:МЦНМО, 1999.-960 с.