10. Минимальные покрывающие деревья

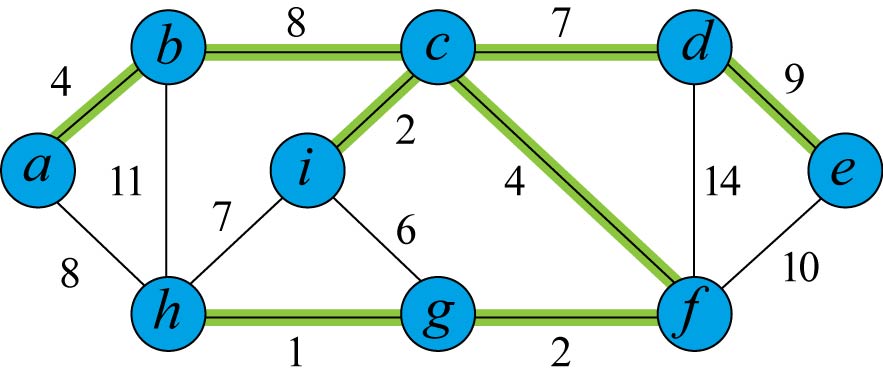
Рис. 24.1 Минимальное покрывающее дерево. На каждом ребре графа указан вес. Выделены ребра минимального покрывающего дерева (суммарный вес 37). Такое дерево не единственно: заменяя ребро (b,c) ребром (a,h), получаем другое дерево такого же веса 37.

Generic-MST(G,w)

1 A ← Ø

2 while (пока) A не является остовом

3 do найти безопасное ребро (u,v) для А

4 А ← А U {(u,v)}

5 return A

Теорема 24.1 Пусть G=(V,E) – связный неориентированный граф, на множестве вершин которого определена вещественная функция w. Пусть А – множество ребер, являющееся подмножеством некоторого минимального остова графа G. Пусть (S,V\S)- разрез графа G, согласованный с А, а (u,v)-легкое ребро для этого разреза. Тогда ребро (u,v) является безопасным для А

Алгоритм Крускала

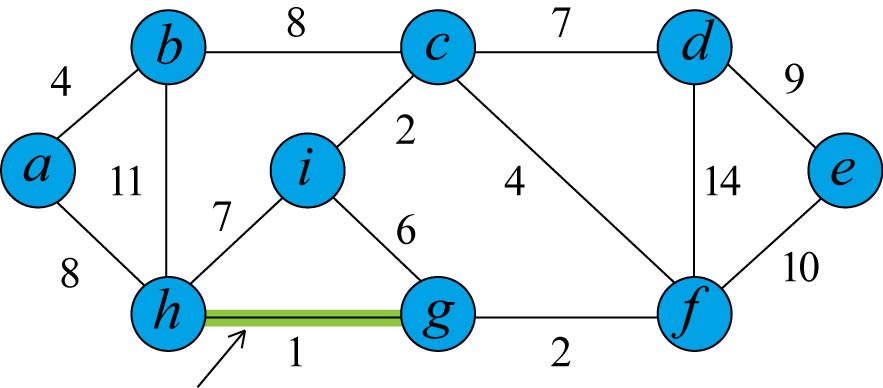
MST-Kruskal(G,w)

1 A ← Ø

2 for (для) каждой вершины vЄV[G]

3 do Make-Set(v)

4 упорядочить ребра Е по весам

5 for (для) (u,v) ЄЕ (в порядке возрастания веса)

6 do if Find-Set(u) ≠ Find-Set(v)

7 then А ← А U {(u,v)}

8 Union(u,v)

9 return A

Алгоритм Прима

MST-Prim(G,w,r)

1 Q ← V[G]

2 for (для) каждой вершины u Є Q

3 do key [u] ←∞

4 key [r] ←0

5 π [r] ←NIL

6 while Q ≠ Ø

7 do u←Exstract-Min(Q)

8 for (для) каждой вершины v Є Adj[u]

9 do if v Є Q и w(u,v) < key[v]

10 then π [v] ←u

11 key[v] ← w(u,v)

11. Поиск в глубину

Стратегия поиска в глубину – идти «вглубь», пока это возможно, и возвращаться и искать другой путь, когда таких ребер нет.

Так делается, пока не обнаружены все вершины, достижимые из исходной.

Если после этого остаются необнаруженные вершины, можно выбрать одну из них и повторять процесс, пока не обнаружим все вершины графа.

Обнаружив впервые вершину v, смежную с u, мы отмечаем это событие, помещая в поле  [v] значение u.

Получается подграф предшествования (лес поиска в глубину), определенный так:G_= (V, E_), где

E_ = {([v],v) : v V и  [v]  NIL}

Алгоритм поиска используют цвета вершин.

Вначале каждая вершина – белая.

Будучи обнаруженной она становится серой.

Когда вершина полностью обработана (просмотрен список смежных с ней вершин), она становится черной.

При поиске в глубину на вершинах ставят метки времени.

Каждая вершина имеет две метки:

d[v] –вершина обнаружена (и сделана серой)

f[v] – закончена обработка (стала черной)

В процедуре DFS (поиск в глубину) метки времени – целые числа от 1 до 2 V.

Для любой вершины u выполняется неравенство

d[u] < f[u]

Исходный граф может быть ориентированным или неориентированным.

Переменная time – глобальная переменная текущего времени

DFS(G)

1 for (для) всех вершин u  V[G]

2 do color[u]  БЕЛЫЙ

3  [u]  NIL

4 time  0

5 for (для) всех вершин u  V[G]

6 do if color [u] = БЕЛЫЙ

7 then DFS-VISIT (u)

DFS-VISIT (u)

1 color [u] = СЕРЫЙ

2 d[u]  time  time + 1

3 for (для) всех v  Adj [u]

4 do if color [v] = БЕЛЫЙ

5 then [v] = u

6 DFS-VISIT (v)

7 color [u] = ЧЕРНЫЙ

8 f[u]  time  time + 1

Классификация ребер

Ребра графа делятся на несколько категорий в зависимости от их роли при поиске в глубину.

Пусть мы провели поиск в глубину на графе G и получили лес G_.

1. Ребра деревьев(tree edges) – это ребра графа .

2. Обратные ребра (Back edges) – это ребра (u,v ), соединяющие вершину u с ее предком v в дереве поиска в глубину. Ребра-циклы, возникающие в ориентированных гоафах, считаются обратными ребрами.

3. Прямые ребра (Forward edges) соединяют вершину с ее потомком, но не входят в дерево поиска в глубину.

4. Перекрестные ребра (Cross edges) – все остальные ребра графа.

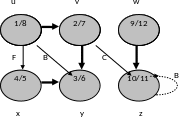
Пример исполнения алгоритма DFS

Пример графа

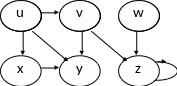
Шаг1

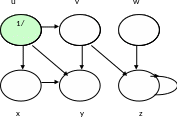
Шаг 2

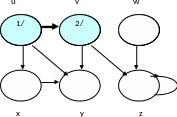
Шаг 3

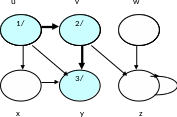
Шаг 4

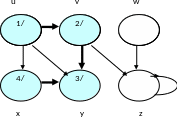
Шаг 5

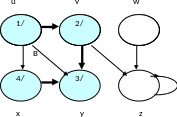
Шаг 6

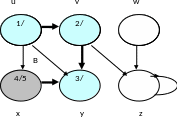
Шаг 7

Шаг 8

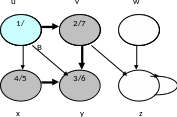
Шаг 9

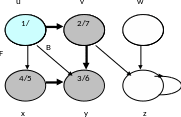
Шаг 10

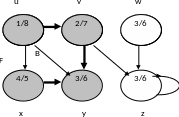
Шаг 11

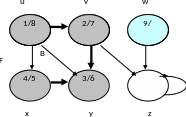
Шаг 12

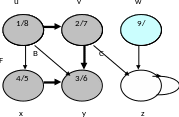
Шаг 13

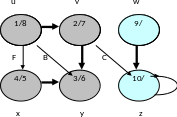
Шаг 14

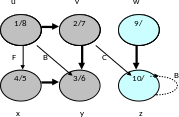
Шаг 15

Шаг 16