Давление жидкости на криволинейные поверхности

С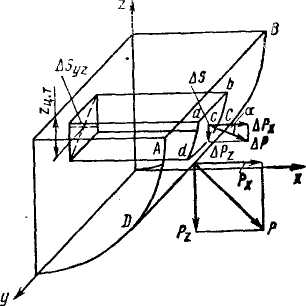 ила избыточного давления, с которой жидкость действует на криволинейную поверхность, находится как геометрическая сумма составляющих по трем взаимно перпендикулярным направлениям: вертикальному и двум горизонтальным. Например, в частном случае, если криволинейная поверхность цилиндрическая (см.рис.) на участок АВ действует сило Р, имеющая две составляющие: горизонтальную Px и вертикальную Pz.

; ; или

,

где h_cx – глубина погружения центра тяжести площади участка АВ;

Sx – площадь проекции поверхности АВ на вертикальную плоскость, перпендикулярную рассматриваемому горизонтальному направлению х;

W – объем тела движения, т.е. объем, ограниченный цилиндрической поверхностью, вертикальными проектирующими плоскостями и поверхностью воды.

Движение идеальной жидкости.

Во всех жидкостях (газах) при движении элементарных слоёв, одних относительно других, возникают силы трения. Если эти силы малы, ими пренебрегают, и тогда, рассматриваемая жидкость (газ) называется идеальной.

Уравнение Бернулли.

Если скорость v и давление P остаются постоянными в каждой точке пространства, где протекает жидкость (газ), то такое движение называют стационарным. В этом случае через любые поперечные сечения трубы жидкость проходит равные объёмы т.е. S₁v₁ = S₂v₂ ,

где S₁ и S₂ – площади двух разных сечений трубы;

v₁ и v₂ – скорости жидкости в этих сечениях.

При изменении сечения трубы и установившемся течении жидкости меняется не только скорость, но и давление, поэтому в любом сечении I-I и II-II (см. рис.) выполняется условие:

I II

v₁ v₂

P₁ P₂

I II

Частным случаем закона сохранения энергии является уравнение Даниила Бернулли (1700-1782г.), которое служит основой гидравлических расчётов. Оно характеризует постоянство суммы геометрического, пьезометрического, скоростного напоров вместе с потерями энергии на преодоление гидравлических сопротивлений по всему тракту движения жидкости.

,

где Z - геометрический напор, определяемый высотой положения места приёма жидкости.

Р/ρ - пьезометрический напор, характеризующий энергию давления среды на жидкость;

v²/2g - скоростной напор, характеризующий скорость истечения жидкости в определённом сечении трубы;

∑ h_w - потери напора на преодоление сопротивлений в трубопроводах.

И з этого следует закон Торричелли: ,где H

v 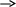- скорость жидкости при вытекании из малого отверстия емкости; v

H - высота поверхности жидкости над отверстием (см. рис.).

Движение вязкой жидкости.

При движении в жидкости любого твёрдого тела, сила, действующая на него внутри вязкой среды, и направленная противоположно скорости тела – называется сопротивлением среды. Если за телом не возникает завихрений, то сопротивление среды пропорционально скорости тела.

Число Рейнольдса (Re) – безразмерный критерий механического подобия, характеризующий течение вязкой жидкости в трубопроводе. Физический смысл критерия Рейнольдса выражает отношение двух эффектов: сил инерции (подвижность жидкости) и силы вязкости. ,

где d – диаметр трубопровода

υ – коэффициент кинематической вязкости

При одинаковых величинах Re жидкость, текущая в трубах разных диаметров и с разными скоростями, имеет одинаковые гидравлические характеристики.

Если число Рейнольдса меньше критической величины (Re _кр1=900-1600) – режим течения ламинарный (спокойный). Если число Рейнольдса больше (Re_кр2=2600-3600) – режим течения турбулентный (с завихрениями потока). В диапазоне между величинами Re_кр1 и Re_кр2 находится переходный режим течения (10⁴>Re>2300), т.е. как ламинарный, так и турбулентный.

В частном случае, при движении шара сопротивление среды можно определить по формуле Стокса: ,

где - коэффициент внутреннего трения жидкости – вязкость, которая в значительной степени зависит от температуры среды.

R - радиус шарика.

Скорость равномерного падения шарика в вязкой среде

где ρ - плотность шарика;

ρ_ж - плотность вязкой среды.

Объём жидкости, протекающей в единицу времени по капилярной трубке радиуса R и длиной l, при поддержании на её концах разности давлений (∆P) - будет равен: