Задание 3. Решение задачи линейного программирования графическим методом.
Дано:
F=2Х1+3Х2 max;
Х1
≥ 4
Х2 ≥3
Х1+Х2 ≤ 8
Х1,Х2 ≥0
Решение.
В ограничениях задач линейного программирования заменяем знаки неравенств на знаки уравнений и строим соответственно прямые.
Х1
= 4
Х2 =3
Х1+Х2 = 8
Вычисляем координаты точек пересечения этих прямых с осями координат.
1-я прямая: Х1=4
2-я прямая: Х2=3
3
-я
прямая: Х1=0 Х1=8
Х2=8 Х2=0
Находим и штрихуем полуплоскости, разрешенные каждым из ограничений неравенств задачи. Для этого подставляем в конкретное неравенство координаты, какой либо точки и проверяем истинность полученного неравенства. Если неравенство истинное, то надо заштриховать полуплоскость, содержащую данную точку, иначе надо заштриховать полуплоскость, не содержащую данную точку.
Определяем область допустимых решений как часть плоскости принадлежащей одновременно всем разрешенным областям и выделяем ее. При отсутствии области допустимых значений - задача не имеет решений. Общей областью, разрешенной всеми ограничениями, является треугольник АВС.
Так как в нашем случае область допустимых решений не пустое множество, то строим целевую прямую С1Х1+С2Х2=F, где F - кратное число С1 и С2.
Целевая прямая: 2Х1+3Х2 =6
Координаты точек пересечения этой прямой с осями координат.
Х
1=0 Х1=3
Х2=2 Х2=0
Строим вектор С, который начинается в точке (0;0) и заканчивается в точке (2;3). Если целевая прямая и вектор С построены верно, то они будут перпендикулярны.
При поиске максимума целевой функции передвигаем целевую прямую в направлении вектора С, при поиске минимума- против направления вектора С. Последняя по ходу движения вершина ОДР будет точкой максимума целевой функции, точка В- точка максимума целевой функции при пересечении 1-й и 3-й прямых.
Определяем координаты точки максимума целевой функции Х*(Х1*;Х2*) и вычисляем значение F(Х*). Для вычисления координат оптимальной точки Х* решаем систему уравнений прямых, на пересечении которых находится Х*.
Х
1=4
Х1=4
Х1+Х2=8 Х2=4
F(Х*) =F(4;4) = 2∙Х1*+3∙Х2*=2∙4+3∙4=8+12=20
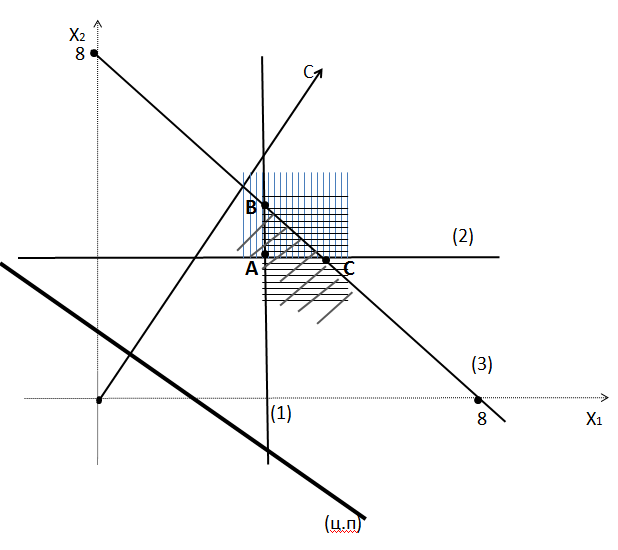
Рисунок 1 – Графическое решение задачи
Задание 4. Решение задачи симплекс-методом.
Дано:
L
=
Х1+2Х2+3Х3-Х4;
Х1+Х2+Х3+Х4=4;
Х1+2Х2+Х3+2Х4=6;
Х1+2Х2+2Х3+Х4=6;
Х1,Х2,Х3,Х4 ≥0
Решение.
Решение задачи ЛП симплекс-методом состоит из 2х этапов:
Находят какой-либо начальный опорный план Х0;
По специальным правилам переходят от начального плана Х0 к другому, более близкому к оптимальному, опорному плану Х1, затем к следующему Х2, и так до тех пор, пока задача не будет решена.
Записываем задачу линейного программирования в форме симплексной таблицы. Последняя строка в симплексной таблице – строка для целевой функции (ЦФ) – f-строка. Все элементы столбца свободных членов должны быть неотрицательны. Те уравнения системы, в которых свободные члены отрицательны, предварительно умножаются на (-1).
Симплексную таблицу преобразовываем шагами жордановых исключений, замещая нули в левом столбце соответствующими х. В ходе жордановых исключений столбцы под «переброшенными» на верх таблицы нулями (разрешающие столбцы) можно вычеркивать.
Если система ограничительных уравнений совместна, то через некоторое число шагов все нули в левом столбце будут замещены на х и так будет получен опорный план.
Таблица 2 Таблица 3
-
1
-Х1
-Х2
-Х3
-Х4
0
4
1
1
1
1
0
6
1
2
1
2
0
6
1
2
2
1
f
0
-1
-2
-3
1
1
-Х1
-Х2
-Х3
-Х4
4
1
1
1
0
-2
-1
0
-1
0
-2
0
1
1
f
-4
-2
-3
-4
Таблица 4 Таблица 5
|
1 |
-Х1 |
-Х2 |
-Х4 |
2 |
1 |
0 |
0 |
0 |
-1 |
1 |
-Х3 |
2 |
0 |
1 |
F |
4 |
-2 |
1 |
|
1 |
-Х1 |
-Х4 |
2 |
1 |
-Х2 |
0 |
-1 |
-Х3 |
2 |
1 |
F |
4 |
-1 |
При Х1 =0, получим Х2 =0, Х3 =2, Х4 =2, тогда f(Х0) =4
Нахождение оптимального опорного плана.
Так как в столбце свободных членов есть отрицательные числа, мы выбираем строку целевой функции, и столбец с отрицательным числом берем за разрешающий, далее делаем еще шаг жорданова исключения.
Таблица 6
|
1 |
-Х3 |
-Х4 |
0 |
|
-Х2 |
2 |
|
-Х1 |
2 |
|
f |
6 |
1 |
Так как в f- строке нет отрицательных элементов (не считая свободного члена) - план оптимален.
Х*(2; 2; 1; 0) f(Х*) =6
Вывод: Решили задачу симплекс- методом.