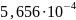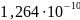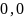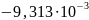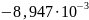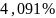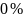4.2. Метод Рунге-Кутта.

Рис. 10. Начальные условия и основные параметры, необходимые для решения уравнения методом Рунге-Кутта.

Рис. 11. Решение уравнения методом Рунге-Кутта.

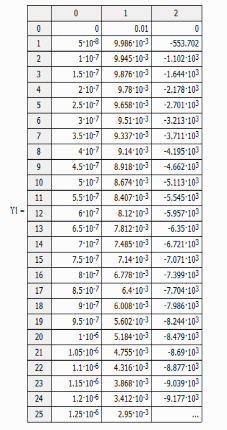
Рис. 12. Точки решения уравнения.

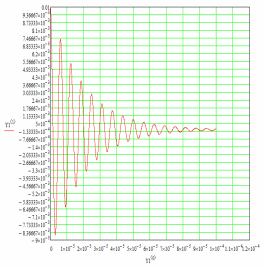
Рис. 13. График зависимости .

Колебания, протекающие по закону косинуса:

. По графику можно вычислить:

А,

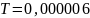с,

Гц,

Гц.

При решении уравнения методом Рунге-Кутта получаем гармонические затухающие колебания (рис. 13), идентичные полученным в методе Эйлера (рис. 5, 8), так что описывать их снова не будем.

Рис. 14. Уменьшение шага решения.

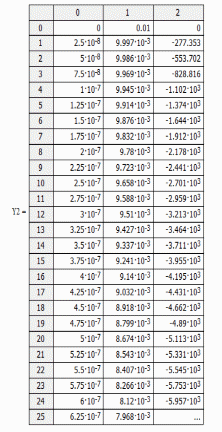
Рис. 15. Новые точки решения уравнения.

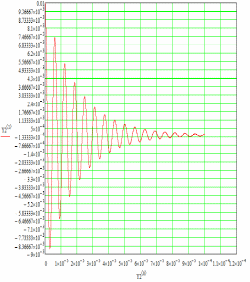
Колебания, протекающие по закону косинуса:

. По графику можно вычислить:

А,

с,

Гц,

Гц.

Рис. 16. Новый график зависимости .

Очевидно, что в методе Рунге-Кутта при изменении шага график функции кардинально не меняется (рис. 16).

Рис. 17. Вычисление погрешности метода Рунге-Кутта.

5. Вывод.

Таблица 2. Сравнение погрешностей методов.

Название метода	Максимальная погрешность
Метод Эйлера
Метод Рунге-Кутта 4-ого порядка
Идеальное значение погрешности

Таблица 3. Сравнение относительных погрешностей методов по элементам.

Методы	Элемент при обычном шаге 0,00000005	Элемент при вдвое меньшем шаге 0,000000025	Относительная погрешность
Метод Эйлер
Метод Рунге-Кутта 4-ого порядка

В ходе данной лабораторной работы я выяснил, что метод Эйлера пригоден для расчета только в том случае, если допускается большая погрешность. Метод Рунге-Кутта дал меньшую погрешность, поэтому я бы рекомендовал его для инженерных вычислений.

6. Список литературы.

1. Леонов В.М. Методические указания к курсовой работе по дисциплине «Численные методы решения задач строительства автодорог» (Электронный курс): кафедра ССМиК, ТулГУ, 2012.

2. Березин И.С., Жидков Н.П. Методы вычислений: том второй: Государственное издательство физико-математической литературы. – 1959 г., 620 с. (с. 286-327).

3. Сайт www.exponenta.ru.