Министерство образования и науки РФ.

Государственное бюджетное образовательное учреждение

высшего профессионального образования.

Тульский государственный университет.

Кафедра «Строительство, строительные материалы и

конструкции».

Курсовая работа

по дисциплине «Численные методы» на тему:

«Численные методы решений задач строительства автодорог».

Вариант № 8-3.

Выполнил ст. гр. 331701 Егоров

Проверил   Леонов В.М.

Тула 2012

Содержание.

1. Введение………………………………………………………….…3

2. Теоретические сведения…………………………………………....3

3. Задание……………………………………………………….……...6

4. Решение задания в MathCAD………………………………….…..7

4.1. Метод Эйлера………………………………………….….…8

4.2. Метод Рунге-Кутта четвертого порядка…………….….…13

5. Вывод……………………………………………………………..….18

6. Список литературы………………………………………………....19

1. Введение.

Цель работы: овладеть численными методами решения задач строительства автодорог.

Для достижения цели необходимо решить ряд промежуточных задач:

1. Изучить теорию и практические аспекты применения метода Эйлера.

2. Изучить теорию и практические аспекты применения метода Рунге-Кутта четвертого порядка.

3. Решить исходную задачу каждым методом.

4. Провести сравнительный анализ методов.

5. Выбрать наиболее точное решение.

6. Сделать вывод о проделанной работе.

2. Теоретические сведения.

Метод Рунге-Кутта - одношаговый метод численного решения задачи Коши для системы обыкновенных дифференциальных уравнений вида 

 (1)

Основная идея метода была предложена К. Рунге и развита затем В. Кутта и другими. Первоначально эта идея использовалась лишь для построения явных схем метода, которые разыскивались в виде 

 (2)

где 

при этом значения постоянных A_i, a_n, b_nm, i=l, 2,...,.q; n=2, 3, . . ., q; m=1, 2, . . ., n-1, определялись из требования, чтобы погрешность равенства (2) на точном решении уравнения (1) имела возможно высокий порядок малости в сравнении с шагом t для любых уравнений вида (1).

В отличие от Адамса метода и других многошаговых методов, метод Рунге-Кутта, как и всякий одношаговый метод, не требует предварительного построения начала таблицы значений приближенного решения и дает возможность вести вычислительный процесс при естественных для уравнения (1) начальных условиях, что позволяет использовать его непосредственно и в случае неравномерных сеток. Однако поскольку в этом методе не используется информация о решении в предыдущих узлах сетки, то он, вообще говоря, оказывается локально менее экономичным, чем, например, метод Адамса.

Наиболее широко известным среди методов Рунге-Кутта является метод 

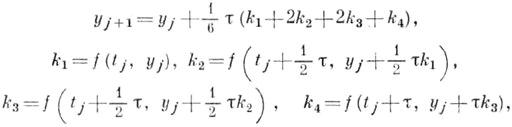
принадлежащий зависящему от двух свободных параметров семейству методов четвертого порядка точности вида (2) с q=4. Популярен и простейший явный метод первого порядка точности, получающийся из (2) при q=1. Этот метод известен под названием метода Эйлера. При значениях q, равных 2 и 3, из (2) могут быть найдены семейства метода Рунге-Кутта второго и третьего порядка точности, зависящие от одного и двух свободных параметров соответственно. В случае q> 4 имевшее место ранее соответствие между значением q и порядком точности метода уже нарушается. Метод Рунге-Кутта вида (2) пятого порядка точности удается построить лишь при q=6, шестого - при q=7, седьмого - при q=9 и т. д. В этом случае с увеличением значения qна единицу расширение множества подлежащих выбору в (2) постоянных A_i, a_n, b_nm часто оказывается уже недостаточным, чтобы удовлетворить условиям, возникающим из требования повышения на единицу порядка точности явного метода. С целью увеличения числа выбираемых в (2) параметров можно рассмотреть, например, следующее обобщение конструкции одношаговых

методов, основанных на идее К. Рунге:

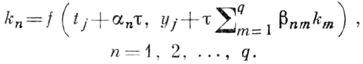 (3)

Методы вида (2), (3) в общем случае являются уже неявными, что значительно осложняет их численную реализацию: величины k_n, n=1, 2, . . . , q, на каждом шаге приходится находить из системы, вообще говоря, нелинейных уравнений (3). Однако за счет достигнутого здесь значительного увеличения числа подлежащих выбору констант такие методы приобретают следующее свойство: для каждого значения q существует неявный метод Рунге-Кутта порядка точности 2q. Кроме того, при таком расширении класса появляются методы, хорошо ориентированные на случай жестких дифференциальных систем.

Имеется еще одно видоизменение идеи К. Рунге конструирования одношаговых методов численного решения уравнений вида (1). Именно, исходя из (1) записывается равенство 

Приближенное представление последнего интеграла квадратурной формулой с q узлами дает 

 (4)

Если выбор узлов a_i и коэффициентов A_i, i=l, 2, . . . , q, рассматриваемой квадратурной формулы подчинить условиям 

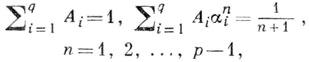 (5)

то погрешность приближенного равенства (4) будет величиной порядка t^p + 1. При   система уравнений (5) разрешима и приближенное равенство (4) может быть построено. Аналогично можно записать приближенные равенства для неизвестных величин u(t_j+a_it), входящих в правую часть (4), при этом требования к их точности могут быть понижены на порядок, и т. д. В качестве примера так построенного одношагового метода ниже приводится (см. [6]) метод третьего порядка точности предсказывающе-исправляющего характера:

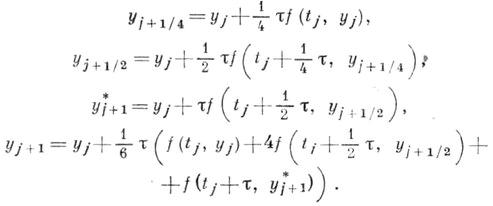
Если положить в (4) одно из значений a_i- равным единице, на этом пути можно строить также и неявные методы, напр. метод 

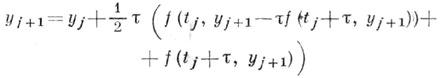
второго порядка точности.

Рассмотренные выше на примере уравнений вида (1) подходы к построению численных методов могут быть распространены на обыкновенные дифференциальные уравнения высших порядков, а также использованы при конструировании разностных схем в случае дифференциальных уравнений с частными производными.