3.6. Решение задачи оптимального управления линейным объектом по минимуму квадратичного функционала в векторно-матричной форме.
Постановка задачи.
Задан объект :
,
(3.89)
где
;
.
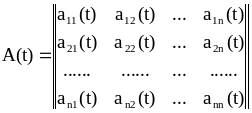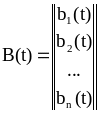(3.90)
Задан функционал :
,
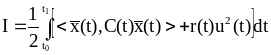(3.91)
где
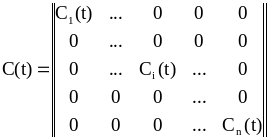
Решение задачи.
Функция F* в уравнение Эйлера имеет следующий вид.
(3.92)
(3.93)
(3.94)
Оптимальное управление :
(3.95)
Каноническая система :
(3.96)
3.7. Решение задачи оптимального управления линейным объектом по минимуму квадратичного функционала при постоянных параметрах.
Решение задачи существенно упрощается в случае, когда рассматривается объект с постоянными параметрами при бесконечном времени управления. При этом также предполагается, что коэффициенты функционала постоянны.
Постановка задачи.
Задан объект :
(3.97)
Задан функционал :
(3.98)
Каноническая система :
(3.99)
Делаем замену :
(3.100)
Отсюда
,
(3.101)
где
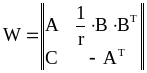(3.102)
Составляем характеристическое уравнение.
(3.103)
(3.104)
(3.105)
Анализ показывает, что распределение корней характеристического уравнения (3.105) на комплексной плоскости будет симметричным как относительно действительной, так и относительно мнимой осей (рис.3.2).
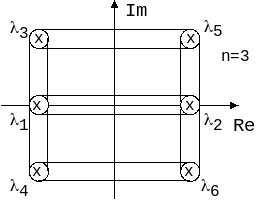
Рис. 3.2. Симметричное распределение корней для объекта 3-го порядка.
Предположим, что среди корней характеристического уравнения есть только действительные корни. Тогда решение для каждой компоненты вектора состояния запишется в виде :
,
(3.107)
Поскольку полученная система должна быть устойчивой должно выполняться следующие :
.
(3.108)
Отсюда
.
(3.109)
В следствии условия (3.109) решение (3.107) будет содержать n произвольных постоянных. Иными словами в канонической системе остаются известными только величины связанные с начальными условиями по компонентам вектора состояния. В этом случае процедура поиска начальных условий по сопряженным переменным исключается.
Пример 3.3.
Требуется определить стационарную обратную связь для объекта управления с передаточной функцией :
,
.
При заданном минимизируемом функционале :
Решение задачи.
1. Записать уравнение состояния и каноническую систему.
2. Найти решение системы для x(t) и (t).
3. Определить оптимальное управление используя переменную (t).
4. Определить коэффициент обратной связи.
1.
, 
, 
, 
.
2. 
3.
4. 
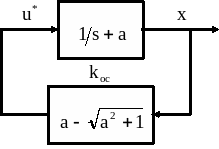
Рис. 3.3. Структурная схема оптимального управления.
Пример 3.4.
Требуется для объекта управления
определить стационарную обратную связь по координатам состояния x1, x2, которая минимизирует функционал
при заданных начальных условиях
Решение задачи.
1.
, 
, 
, 
.
2.
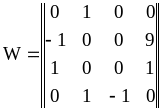
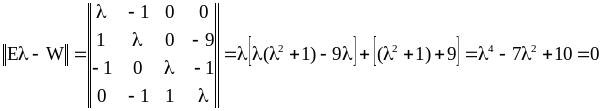
Отсюда
, 
.
Делаем замену
, 
3. 
4. 
, 
.