2.2. Уравнение Эйлера
Уравнение Эйлера определяет необходимое условие существования экстремума функционала следующего вида:
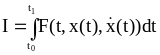(2.21)
где F - некоторая дифференцируемая по своим аргументам функция. Предполагается, что левая и правя точки экстремали заданы:
(2.22)
Рис. 2.5. Задача
Эйлера.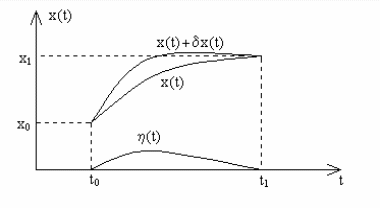
(2.23)
(2.24)
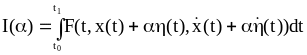(2.25)
(2.26)
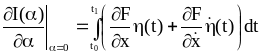(2.27)
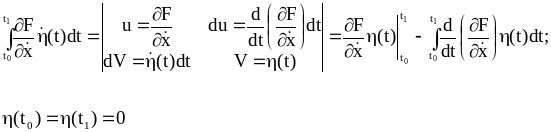(2.28)
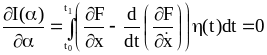(2.29)
(2.30)
Уравнение Эйлера представляет собой дифференциальное уравнение второго порядка, с заданными левой и правой граничными точками.
Пример 2.1.
Требуется определить экстремаль функционала
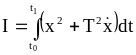проходящего
через точки
.
Решение задачи.
;
Пример 2.2.
Требуется определить экстремаль функционала:
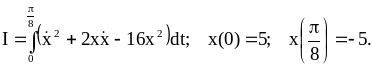
Решение задачи.
2.3. Уравнение Эйлера для функционала, содержащего векторную переменную.
Рассмотрим функционал:
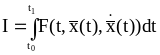(2.31)
где
(2.32)
Технология решения задачи, в принципе, не отличается от ранее рассмотренного случая.
(2.33)
Полагаем, что
существуют частные производные F по
всем компонентам
и
.
(2.34)
В данном случае (2.34) будет системой дифференциальных уравнений порядка 2n.
2.4. Естественные граничные условия.
В ряде задач рассматривается случай, когда у искомой экстремали зафиксирована лишь левая граничная точка, а для правой граничной точке указан лишь параметр t1
Рис. 2.6.
Естественные граничные условия.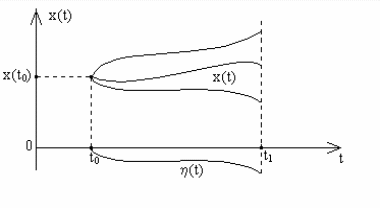
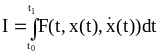(2.35)
(2.36)
Очевидно, что
при любых вариациях, а
:
(2.37)
(2.38)
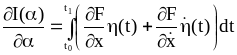(2.39)
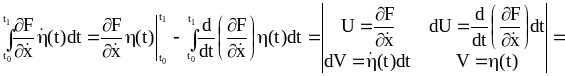
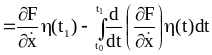(2.40)
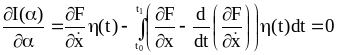(2.41)
(2.42)
(2.43)
Естественные граничные условия налагают дополнительные требования на поведение искомой экстремали в правой граничной точке.
Пример 2.3.
Задан функционал:
.
;
;
;
;
;
;
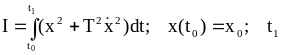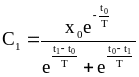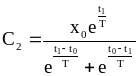
2.5. Граничные условия для функционала вида:
В данной задаче не зафиксированы левая и правая граничная точки, а t0 и t1 заданы.
Предполагается,
что функции
и
дифференцируемые по своим переменным.
Рис. 2.7. Граничные
условия для функционала вида:
(2.44)
(2.45)
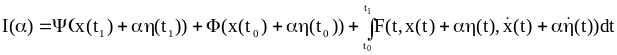(2.46)
(2.47)
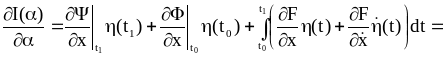
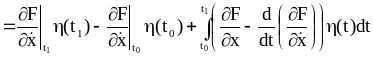(2.48)
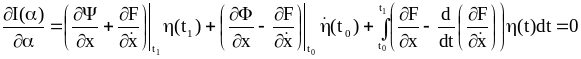(2.49)
(2.50)
(2.51)
(2.52)
Таким образом, решение поставленной задачи состоит в решении уравнения Эйлера. Причем искомая экстремаль должна удовлетворять граничным условиям (2.51) и (2.52) соответственно для правой и левой граничных точек.
Пример 2.4.
Требуется определить экстремаль функционала
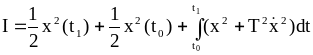
при заданных t0 и t1.
Решение задачи.
; 
;
; 
;
; 
;
