
- •1. Введение
- •1.1. Математическая модель системы (объекта управления)
- •1.2. Математическая модель линейного объекта
- •1.3. Постановка общей задачи оптимального управления
- •1.4. Частные случаи общей задачи оптимального управления
- •1.5. Методы решения задач оптимального управления
- •2. Вариационные методы решения задач оптимального управления
- •2.1. Элементы вариационного исчисления
- •2.2. Уравнение Эйлера
- •2.3. Уравнение Эйлера для функционала, содержащего векторную переменную.
- •2.4. Естественные граничные условия.
- •2.5. Граничные условия для функционала вида:
- •2.6. Общая форма первой вариации.
- •2.6. Уравнение Эйлера–Пуассона.
- •2.7. Вторая вариация функционала. Условие Лежандра.
- •3. Определение экстремали функционала при наличии ограничений.
- •3.1. Изопериметрическая задача.
- •3.2. Условный экстремум функционала.
- •3.3. Экстремум функционала при наличии ограничений в форме дифференциальных уравнений.
- •3.4. Некоторые сведения из алгебры матриц и квадратичных форм.
- •3.5. Оптимальное управление линейным объектом по минимуму квадратичного функционала.
- •3.6. Решение задачи оптимального управления линейным объектом по минимуму квадратичного функционала в векторно-матричной форме.
- •3.7. Решение задачи оптимального управления линейным объектом по минимуму квадратичного функционала при постоянных параметрах.
- •3.8. Задача Майера.
- •3.9. Задача Больца.
- •3.10. Решение уравнения состояния для линейного объекта.
- •3.11. Некоторые свойства фундаментальной матрицы.
- •3.12. Методы получения фундаментальных матриц.
- •3.13. Необходимое условие оптимальности в задачи управления линейным объектом первого порядка. Функция Гамильтона.
1. Введение
1.1. Математическая модель системы (объекта управления)
Рис. 1.1. Структурная
схема системы управления.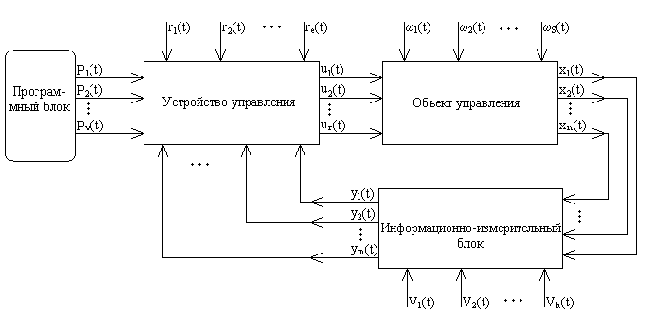
![]() (1.1)
(1.1)
или, в матричной форме:
![]() (1.2)
(1.2)
где
![]() (1.3)
(1.3)
Информационно–измерительный блок также может быть динамической системой, которая описывается соответствующей системой дифференциальных уравнений.
![]() (1.4)
(1.4)
Часто информационно–измерительный блок представляется в виде системы нелинейных алгебраических уравнений.
![]() (1.5)
(1.5)
Программный блок определяет как требуемые функции, определяющие требуемое состояние объекта, так и алгоритмы. Он функционирует на основании программы, заложенной оператором. В принципе, программный блок может быть связан и с информационно–измерительным блоком, поскольку алгоритм управления и программные функции pi(t) могут изменятся в зависимости от состояния объекта.
1.2. Математическая модель линейного объекта
Линейный объект описывается следующими уравнениями:
 (1.6)
(1.6)
![]() (1.7)
(1.7)
1.3. Постановка общей задачи оптимального управления
Задан объект:
![]() (1.8)
(1.8)
Исходное состояние:
![]() (1.9)
(1.9)
Конечное состояние:
![]() (1.10)
(1.10)
Ограничение на состояние:
![]() (1.11)
(1.11)
Ограничение на управление:
![]() (1.12)
(1.12)
Критерий оптимальности:
 (1.13)
(1.13)
Для объекта управления заданного уравнением состояния (1.8) требуется определить ограниченное по условию (1.12) управление такое, чтобы при переходе объекта управления из состояния (1.9) в состояние (1.10) по ограниченным уравнением (1.11) траекториям, критерий оптимальности (1.13) принимал свое наибольшее или наименьшее значение.
1.4. Частные случаи общей задачи оптимального управления
1. Задачи оптимального быстродействия.
Задан объект управления:
![]() (1.14)
(1.14)
Заданы начальное и конечное состояния:
![]() (1.15)
(1.15)
![]() (1.16)
(1.16)
Заданы ограничения на состояние и управление:
![]() (1.17)
(1.17)
![]() (1.18)
(1.18)
Время движения t1- неизвестно;
Критерий оптимальности:
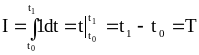 (1.19)
(1.19)
Таким образом в задачах оптимального быстродействия минимизируется время движения.
2. Задача на минимум интегрального критерия.
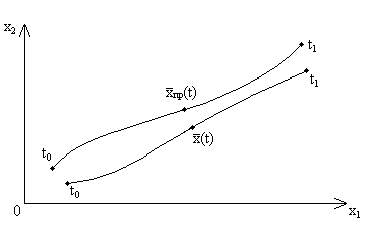 Рис.
1.2. Задача на минимум интегрального
критерия
Рис.
1.2. Задача на минимум интегрального
критерия
Введем в рассмотрение ошибки:
![]() (1.20)
(1.20)
![]() (1.21)
(1.21)
Критерий оптимальности:
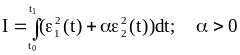 (1.22)
(1.22)
3. Терминальная задача.
Задано начальное состояние x(t0), время движения t1. Конечное состояние x(t1) неизвестно. Критерий оптимальности:
![]() (1.23)
(1.23)
4. Задача на минимум комбинированного функционала.
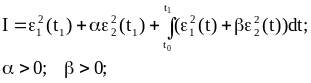 (1.24)
(1.24)
Для n-мерного пространства:
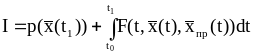 (1.25)
(1.25)
5. Задача аналитического конструирования оптимальных регуляторов.
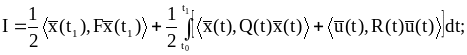 (1.26)
(1.26)
Если F=Q=R=1 и n=1 то:
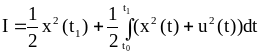 (1.27)
(1.27)
