1. Определение Ме в дискретном рр:

1.1. если число ед. совокупности нечетное, то Ме= значение признака у ед. совокупности с порядковым номером N.

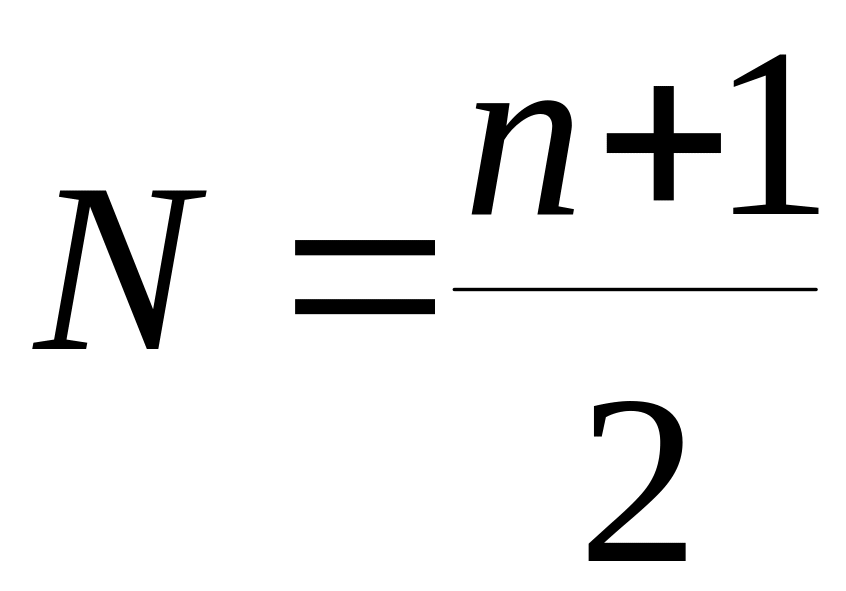
1.2 Если число ед. Совокупности четное, то

n – численность ед. совокупности, N₁= , N₂=

2. Расчет Ме в интервальном ряду р.

, где Х_ме - нижнее значение Ме интервала, h - величина Ме интервала, - сумма частот или численность совокупности, - значения накопленной частоты интервала представленному интервалу, - частота медианного интервала.

Ме интервал- интервал, в котором впервые встечается значение накопленной частоты равное или большее половины численности совокупности.

Мо – знач. признака , которое наиболее часто встречается в совокупности. В дискретном ряду значение Мо очевидно

В интервальном РР Мо рассчитывается по следующей формуле:

х_мо –нижнее значение Мо интервала

h – величина интервала

f_{мо –} частота модального интервала

f_мо-1 – частота интервала, предшествующего модальному

f_{мо+1 –} частота интервала, следующего за модальным

Расчет Мо по данной формуле используется в случае равных интервалов. В случае неравных интервалов необходимо рассчитать плотность распределения.

Мо интервал – интервал, имеющий наибольшую частоту.

На основе данных пок-лей можно сделать выводы о хар-ре распед-ния:

-симметриное,если X=Me=Mo

- правостор.асимметрия X>Me>Mo

- левосторон.асимметрияX<Me<Mo

7. Понятие о квантилях. Порядок расчета квартилей, децилей, сфера применения.

Квантили- структурные показатели, кот-е хар-ют особенности формы распред-ния. К ним относят: медиану, квартили, децили,квинтили.

Квартили – значение признака у тех ед. совокупности, которые делят численность совокупности на 4 равные части.

Интервал,в котором заключен 1 –й квартиль - интервал, в котором впервые встречается значение накопленной частоты равное или большее ¼ от численности совокупности.

Квинтили - значение признака у тех ед. совокупности, которые делят численность совокупности на 5 равн.частей.

Децили - значение признака у тех ед. совокупности, которые делят численность совокупности на 10 равных частей. Квантили нах. применение в соц.статистике для изучения дифференциации населения по уровню доходов. На основе децилей рассчит-тся коэф-нт децильной дифференциации:

K_d= d₉/d₁

На основе квинтилей- квинтильный к-нт:

K=K₄/K₁

Коэф-нт Джини.

8. Показатели формы распределения: к-нт асимметрии и к-нт эксцесса.

К-нт асимметрии:

1) As=(X-Mo)/СКО

если >0,то правосторон.ас-рия

если < 0,то левостор.ас-рия

если = 0.то симметричн.распредление

Для интерпретации результатов исполз.шкалу:

|As|<0,25 – незначит.ас-рия

<=|As|<= - умерен.ас-рия

|As|> - значит. ас-рия

2)As=m₃/СКО³

На основе дан.формулы проводят строгую проверку существенности ас-рии:

если |As|/ сигма_As>3, то ас-рия существенна. Сигма_As- ср.квадр.ошибка к-нта ас-рии.

К-нт эксцесса

E_x=m₄/СКО⁴-3

E_x>0 – островершинное распределение

E_x< - плосковершин.распр-е

E_x=0 – норм.распр-е

Если |E_x|/сигма_ex>3, то существен.

Оценка существенности пок-лей ас-рии и эксцесса позвол. Сделать вывод о том, можно ли данное распраделение отнести к типу кривых нормальн.распр-ния.