Электрические цепи синусоидального тока(s.T.).

Этот ток изменяется во времени по закону синуса или косинуса. Его преимущество перед постоянным: 1)наиболее экономичен,2)в цепях синусоидального тока относительно просто преобразовывать напряжения, получать большее или меньшее значение с помощью трансформаторов, сохраняя при этом форму кривой напряжения (частота).

Получение синусоидального тока.

При вращении металлической рамки в магнитном поле по закону Фарадея: , где - ЭДС самоиндукции.

- магнитный поток. [ ] = Вб, [В] = Тл.

- угол между и .

T – время полного оборота вокруг оси. , чаще используется циклическая частота . [ ]= с^-1.

Приборы, включенные в цепь с переменным напряжением, показывают действующее значения переменной величины. U – действующее значение напряжения, I - действующее значение тока. , , .Средние значения: , .

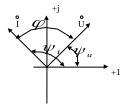
Представление синусоидальных функций в различных формах.

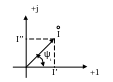Комплексная ось включает действительную часть и мнимую, где j=i= .Переменная величина на комплексной плоскости изображается в виде вектора. или U,I,E,Z – вектора, где I’ – координата по действительной оси. Длина вектора соответствует действительному значению переменной величины. . Данный вектор можно записать в виде комплексного числа, используя алгебраическую запись: или в показательной форме: , где I – длина вектора или действующее значение переменной величины. - угол между действительной осью и вектором.

Перевод алгебраической записи вектора в показательный.

- действующее значение. , если I’ – отрицательна, то к прибавляется .

Перевод показательной записи в алгебраическую.

Известно I и . Определить: I', I’’. I’=I cos , I’’=I cos , .

Переход к записи мгновенного значения переменной величины.

Известно I’ и I’’.Определить: и . , , = , если I’<0, то прибавляем .

Переход от записи мгновенного значения переменной величины к записи вектора в показательной форме.

Дано: I= .Определить: . .

Алгебраические операции с комплексными числами.

A=A’+jA’’= . При сложении и вычитании векторные величины записываем в алгебраической форме. , , .

При умножении и делении векторные величины записываются в показательной форме. , ; A= , где , ; , где A= , .

Основные элементы и параметры электрических цепей синусоидального тока.

1. Резистивный элемент.(Резистор, активное сопротивление).

При прохождении электрического тока через этот элемент в нем выделяется тепло. Q=IUt.

2. Катушка индуктивности. (Индуктивность).

[L] – Гн. Ее называют реактивным элементом, т. к. в ней происходит преобразование энергии электрического тока в энергию магнитного поля. Она представляет собой сопротивление переменному току. ( - индуктивное сопротивление). [ ] – Ом.

3. Емкостное сопротивление.

Также является реактивным, где энергия электрического тока переходит в энергию магнитного поля . - емкостное сопротивление.

4. Полное сопротивление. z= , где - реактивное сопротивление цепи. Полное сопротивление цепи изображают на комплексной плоскости в виде вектора

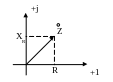
- векторная запись полного сопротивления электрической цепи.

Напряжение и ток на элементах цепи синусоидального тока.

1. Участок цепи с активным сопротивлением.

Г рафик зависимости тока и напряжения Векторная диаграмма тока и на участке с активным сопротивлением. напряжения.

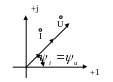
1) ,

2) i= , , . Сдвигом по фазе называется разность между фазой напряжения и фазой тока .Для изображения векторной диаграммы тока выбираем масштаб для тока и напряжения. Для этого надо найти действующие значения тока и напряжения. Если ток и напряжения записываются через комплексные числа, то и , , где , .

2. Индуктивное сопротивление.

Г рафик зависимости тока и напряжения Векторная диаграмма тока и на участке с индуктивным сопротивлением. напряжения.

1)

2) i= , тогда

3) , предположим, что А=0 и , тогда и из 3) следует z= =Lw – индуктивное сопротивление, а , то есть ток отстает по фазе от напряжения на 90 .

В комплексной форме , , = .

3. Емкостное сопротивление.

Г рафик зависимости тока и напряжения Векторная диаграмма тока и на участке с индуктивным сопротивлением. напряжения.

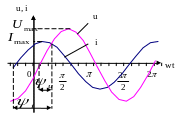
1) , .

2) , тогда , , ток по фазе опережает напряжение. В комплексной форме , , = .

4. Закон Ома для участка цепи с последовательным соединением

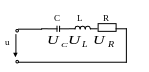
Общее сопротивление равно , а напряжение – сумме падений напряжений на участках цепи. Ток в цепи постоянен.

1) , все расчеты ведутся в комплексной форме. , , тогда из 2) , , .

2) 1): , по закону Ома - полное сопротивление участка цепи с последовательным соединением элементов. Если цепь имеет сложный характер, то необходимо ее разбить на отдельные ветви с последовательным соединением элементов. Каждую ветвь обозначить через соответствующее сопротивление z/ Упрощать схему как при постоянном токе, вычисляя эквивалентные сопротивления в комплексной форме.

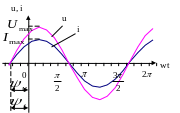
Мощность цепи синусоидального тока.

p=ui – мгновенная мощность.

График зависимости мощности от тока и напряжения.

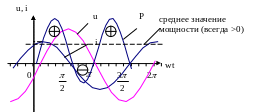
Среднее значение мощности вычисляем через среднее значение активной, реактивной, полной мощности.

1) P – среднее значение активной мощности. , [P]- Вт, .

2) Q – реактивная мощность . , , [Q] = ВАр=Вольт*ампер*реактивное.

3) Полная мощность. , , .

Мощность в комплексной форме.

, где - комплексно-сопряженная величина. , .

По закону сохранения энергии должен выполняться баланс мощности: активная мощность источников должна быть равна активной мощности приемников. Аналогично: реактивная мощность источников равна реактивной мощности приемников.( ).Коэффициентом мощности называют отношение активной мощности к полной мощности , он показывает, какая часть электрической энергии преобразуется в необратимую энергию.

Резонанс в электрических цепях.

Режим работы участка цепи, содержащий L и C, при котором разность фаз между напряжением и током равна 0. Различают резонанс тока и напряжения.

Резонанс напряжения.

, .

, , , . Сопротивление реактивного элемента при резонансной частоте называется характеристическим сопротивлением последовательного контура. , . Отношение характеристического к активному сопротивлению называется добротностью .

Характерные особенности резонанса напряжений:

1) Резонансное сопротивление. , , . Общее сопротивление при резонансе равно активному. Это минимальное сопротивление участка.

2 ) Напряжение на отдельных участках цепи. , ,

График зависимости тока и напряжения от частоты.

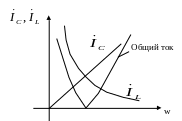
Резонанс токов.

Возникает на участках цепи с параллельным соединением индуктивности и емкости.

Резонансная частота определяется аналогично частоте для резонанса напряжений .

Кривая зависимости проводимости от частоты

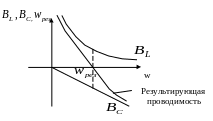
Кривая зависимости токов от частоты