Тема 15(ем). Смеси газов

Вопрос 1. Смеси идеальных газов

В практике часто приходится иметь дело с газообразным веществом, близким по свойствам к идеальным газам и представляющими собой механическую смесь различных газов, химически не реагирующих между собой.

1.1. Давление, объем и масса смеси

Основным законом, определяющим поведение газовой смеси является закон Дальтона: полное давление смеси идеальных газов равно сумме парциальных давлений всех входящих в смесь компонентов

Парциальное давление р_i – это давление, которое имел бы компонент газа, если бы он один при той же температуре занимал весь объем смеси.

Объем смеси идеальных газов равен сумме приведенных (парциальных) объемов всех входящих в смесь компонентов

.

Приведенным (парциальным) объемом называется объем, который занимал бы компонент газа, если бы его давление и температура равнялись давлению и температуре смеси.

.

Масса смеси идеальных газов равна сумме масс всех входящих в смесь компонентов

1.2. Способы задания смеси

Состав смеси может быть задан массовыми, объемными или мольными долями.

Массовой долей называется отношения массы отдельного компонента М_i к массе смеси М

и .

Например, для воздуха  77 %,  23 %.

Объемной долей называется отношения приведенного объема компонента газа V_i к полному объему смеси V.

и .

Для воздуха = 78 %, = 21 %.

Мольной долей называется отношение количества молей N_i рассматриваемого компонента к общему количеству молей смеси N. Можно показать, что задание смеси газов мольными долями равнозначно заданию ее объемными долями

, где .

1.3. Газовая постоянная и молекулярная масса смеси

Уравнение состояния для смеси

или через компоненты смеси

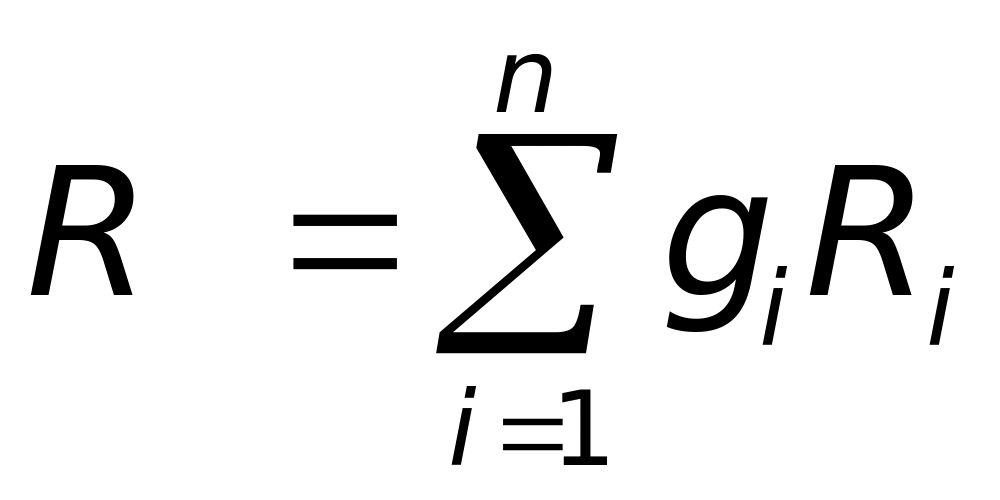= - газовая постоянная смеси.

Молекулярная масса смеси:

1) через массовые доли:

=; .

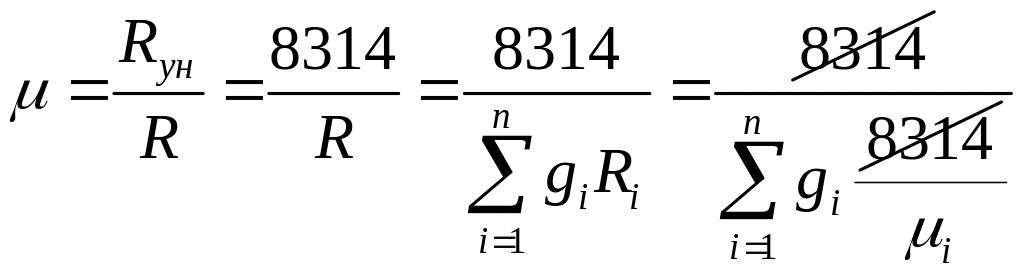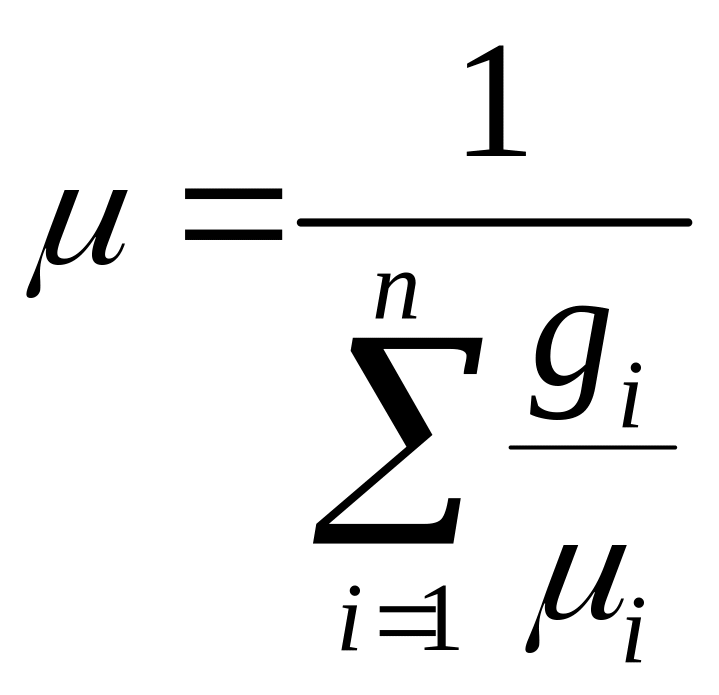2) через объемные доли,

так как , то =

1.4. Соотношения между объемными и массовыми долями

=> и

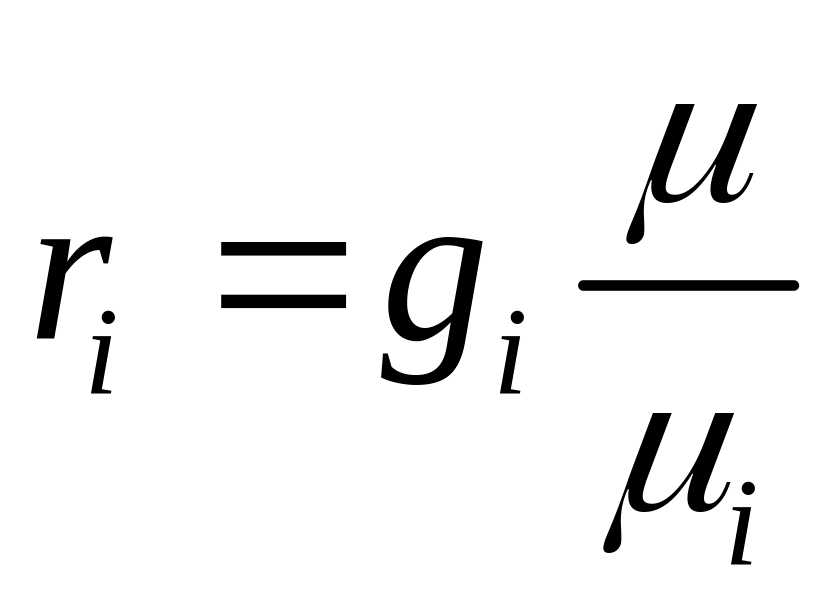
1.5. Теплоемкость смеси

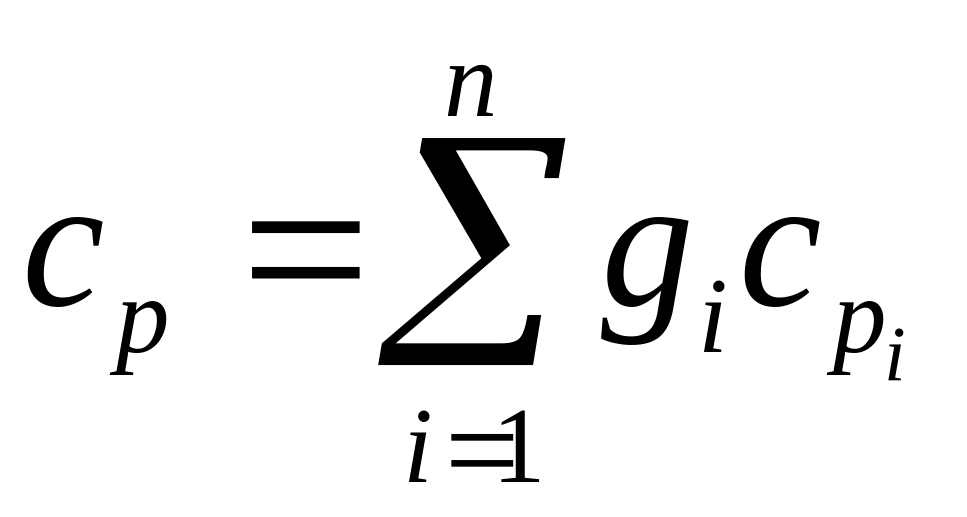; - массовая теплоемкость при v = const и р = const,

; - объемная теплоемкость при v = const и р = const,

; - мольная теплоемкость при v = const и р = const.

1.6. Смешивание идеальных газов при постоянном объеме

Пусть несколько газов с давлениями р₁, р₂, … и температурами Т₁, Т₂, … занимают различные объемы V₁, V₂, …

После удаления разделяющих перегородок объем образовавшейся смеси будет равен сумме объемов смешиваемых газов: .

Масса смеси газов равна сумме масс газов, составляющих смесь:

Предполагается, что при смешение газов отсутствует теплообмен с внешней средой, и газы не совершают внешней работы. В этом случае внутренняя энергия смеси идеальных газов, согласно первому закону термодинамики, равна сумме внутренних энергий отдельных газов до смешения: .

Тогда при получим

.

Откуда температура смеси идеальных газов

= ,

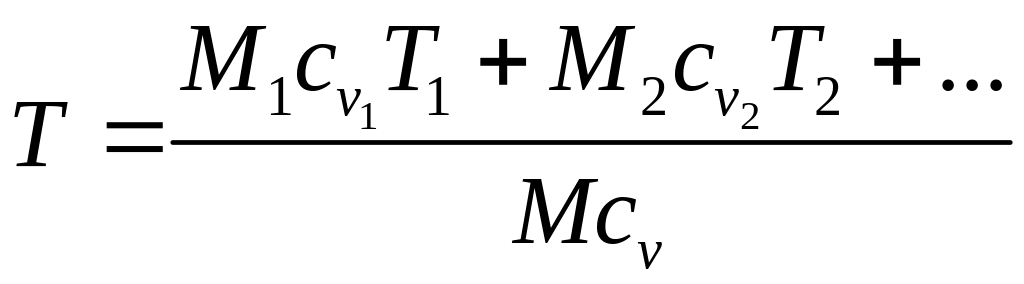где g₁, g₂ и т.д. – массовые доли идеальных газов, составляющих смесь.

Из полученного уравнения и уравнения состояния идеальных газов можно получить давление смеси газов одинаковой атомности

.

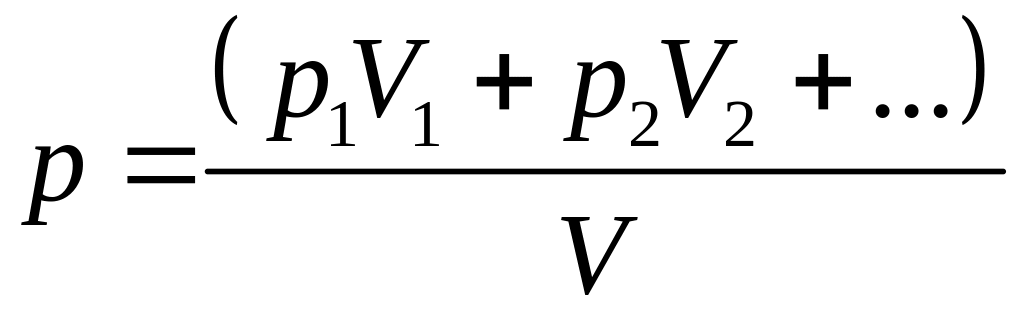Зная температуру, объем и давление, можно определить все остальные величины и параметры смеси газов.