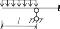
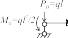- •1.Предмет и задачи см. Основные понятия:расчЁтная схема сооружений,наргрузка,опорные устройства,их статическая и кинематическая характеристики.Классификация расчЁтных схем.
- •9.Статически определимые плоские фермы.РасчЁт способом вырезания узлов.Привести пример.
- •11.Понятие о шпренгельных фермах.Общий порядок расчЁТа.
- •13.Линия влияния усилий в многопролЁтных статически определимых балках.Пример.
- •23. Метод сил. Идея метода сил,основные понятия: лишние связи,условно необходимые и абсолютно необходимые связи, критерии рациональности выбора основной системы.
- •Уравнение трех моментов.
Уравнение трех моментов.
К уравнениям такого типа сводится система канонических уравнений при расчете неразрезной балки по методу сил.
Рассмотрим
многопролетную неразрезную балку
произвольной длины при действии
произвольных внешних воздействий.
Выделим из рассматриваемой балки два
пролета, примыкающие к произвольной
опоре
![]() (рис9.4 а). Будем нумеровать опоры балки
слева направо, начиная с номера
(рис9.4 а). Будем нумеровать опоры балки
слева направо, начиная с номера
![]() .
При этом каждый пролет
.
При этом каждый пролет
![]() и его жесткость
и его жесткость
![]() ,
являющаяся постоянной в пределах
каждого пролета, получают индекс
,
являющаяся постоянной в пределах
каждого пролета, получают индекс
![]() ,
соответствующий номеру правой опоры.
,
соответствующий номеру правой опоры.
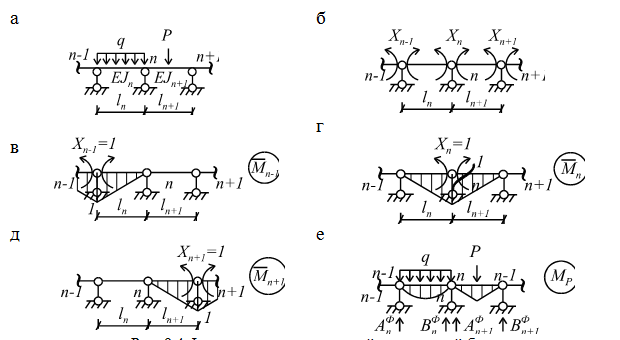
Рис. 9.4 Фрагмент многопролетной неразрезной балки.
Для
расчета балки основную систему метода
сил образуем путем врезания (постановки)
в сечениях над всеми промежуточными
опорами шарниров (рис. 9.4 б). Вместо
устраненных связей приложим неизвестные
опорные моменты
![]() ,
,
![]() ,
...,
,
...,
![]() .
Таким образом, основная система будет
представлять собой ряд простых
независимых однопролетных статически
определимых балок. Единичные эпюры
.
Таким образом, основная система будет
представлять собой ряд простых
независимых однопролетных статически
определимых балок. Единичные эпюры
![]() и грузовая
и грузовая
![]() ,
которые получаются при рассмотрении
каждого пролета как статически
определимой балки, показаны на рис9.4
в-е. Условие неразрывности балки в
местах устраненных связей, т. е. углов
расхождения смежных сечений (углов
перелома) над промежуточными опорами,
записывается в виде системы обычных
канонических уравнений метода сил.
Вычисляя коэффициенты
,
которые получаются при рассмотрении
каждого пролета как статически
определимой балки, показаны на рис9.4
в-е. Условие неразрывности балки в
местах устраненных связей, т. е. углов
расхождения смежных сечений (углов
перелома) над промежуточными опорами,
записывается в виде системы обычных
канонических уравнений метода сил.
Вычисляя коэффициенты
![]() и
и
![]() способом Верещагина с учетом только
изгибных деформаций и учитывая
локальность единичных эпюр
способом Верещагина с учетом только
изгибных деформаций и учитывая
локальность единичных эпюр
![]() в пределах двух смежных пролетов,
получим
в пределах двух смежных пролетов,
получим
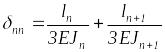 ,
,
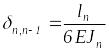 ,
,
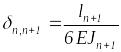 ,
,
![]() ,
,
где
![]() и
и
![]() - площади эпюр изгибающих моментов,
построенные от заданной нагрузки на
примыкающем к опоре
левом и правом пролетах соответственно;
- площади эпюр изгибающих моментов,
построенные от заданной нагрузки на
примыкающем к опоре
левом и правом пролетах соответственно;
![]() - расстояние от левой опоры примыкающего
к опоре
левого пролета до центра тяжести площади
эпюры изгибающих моментов
;
- расстояние от левой опоры примыкающего
к опоре
левого пролета до центра тяжести площади
эпюры изгибающих моментов
;
![]() - расстояние от правой опоры примыкающего
к опоре
правого пролета до центра тяжести
площади эпюры изгибающих моментов
.
- расстояние от правой опоры примыкающего
к опоре
правого пролета до центра тяжести
площади эпюры изгибающих моментов
.
При этом каноническое уравнение метода сил для -й опоры примет вид
![]() .
.
Как
видно,
-е
уравнение системы канонических уравнений
содержит только три неизвестных опорных
момента и поэтому называется уравнением
трех моментов. Подставив в данное
уравнение значения соответствующих
коэффициентов, приведя подобные и
обозначив неизвестные опорные моменты
![]() ,
,
![]() и
и
![]() через
через
![]() ,
,
![]() и
и
![]() соответственно, получим уравнение трех
моментов в развернутом виде
соответственно, получим уравнение трех
моментов в развернутом виде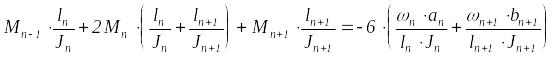
или
![]() ,
(9.3)
,
(9.3)
где
,
,
- величины изгибающих моментов над
опорами
![]() ,
,
![]() ,
,
![]() (моменты считаются положительными,
если вызывают растяжение в нижних
волокнах балки);
(моменты считаются положительными,
если вызывают растяжение в нижних
волокнах балки);
![]() ,
,
![]() - приведенные длины пролетов, вычисленные
по формулам
- приведенные длины пролетов, вычисленные
по формулам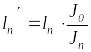 ,
,
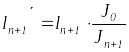 величину
величину
![]() обычно принимают равной моменту инерции
одного из пролетов балки);
обычно принимают равной моменту инерции
одного из пролетов балки);
![]() ,
,
![]() - фиктивные опорные реакции в опоре
от загружения соответствующих пролетов
фиктивной нагрузкой, представляющей
собой эпюру
(рис. 9.4 е). Значения фиктивных реакций
для некоторых наиболее распространенных
видов нагрузки приведены в табл. 1. В
случае балки постоянного сечения (при
- фиктивные опорные реакции в опоре
от загружения соответствующих пролетов
фиктивной нагрузкой, представляющей
собой эпюру
(рис. 9.4 е). Значения фиктивных реакций
для некоторых наиболее распространенных
видов нагрузки приведены в табл. 1. В
случае балки постоянного сечения (при
![]() )
уравнение трех моментов примет вид
)
уравнение трех моментов примет вид
![]() .
(9.5)
.
(9.5)
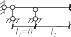
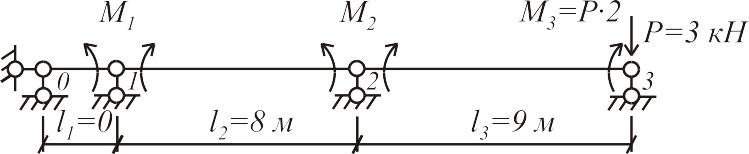
Это уравнение устанавливает связь между величинами опорных моментов в трех соседних опорах неразрезной балки. Если неразрезная балка имеет консоли, то они отбрасываются, а нагрузки с консолей переносятся на опоры в виде силы и момента (рис9.5, а). При наличии жестких заделок они заменяются фиктивными пролетами нулевой длины (рис.9.5, б), которые добавляются к балке со стороны заделки. Например, для балки (рис.9.6, а) расчетная схема (основная система) показана на рис 9.6, б.
а |
|
|
б |
|
|
Рис.9.6 Особенности выбора основной системы для неразрезных балок.
а |
|
б |
|
Рис.9.6 Пример выбора основной системы для двухпролетной неразрезной балки.
Уравнение трех моментов записывается для каждой промежуточной опоры. Решение полученной таким образом системы уравнений определяет величины изгибающих моментов на всех промежуточных опорах неразрезной балки.
Определение внутренних усилий и опорных реакций. Внутренние усилия в сечении любого пролета неразрезной балки выражаются через опорные моменты по концам пролета:
![]() ,
,
![]() ,
,
где
![]() ,
,
![]() - опорные моменты на левом и правом
концах
-го
пролета,
;
- опорные моменты на левом и правом
концах
-го
пролета,
;
![]() - изгибающий момент и поперечная сила
в сечении
- изгибающий момент и поперечная сила
в сечении
![]() однопролетной балки от внешней нагрузки
в
-м
пролете.
однопролетной балки от внешней нагрузки
в
-м
пролете.
Опорные реакции вычисляются по формуле
![]() ,
,
где
![]() ,
,
![]() - поперечные силы слева и справа от
опоры
.
- поперечные силы слева и справа от
опоры
.