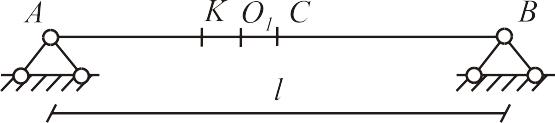13.Линия влияния усилий в многопролЁтных статически определимых балках.Пример.

При построении ЛВ усилий в многопролетных статически определимых шарнирных балках статическим методом удобно пользоваться так называемыми «поэтажными схемами», для того чтобы определить, какая часть балки является основной (главной) по отношению к другим (второстепенным). Напомним, что я.

а
б
в
г
д

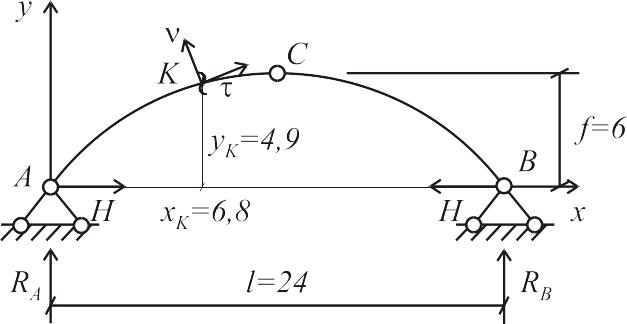
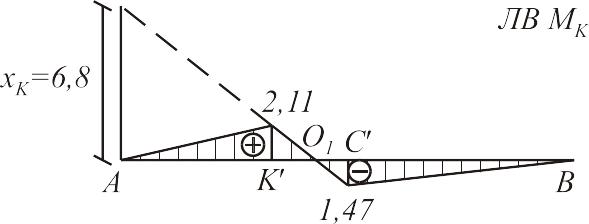
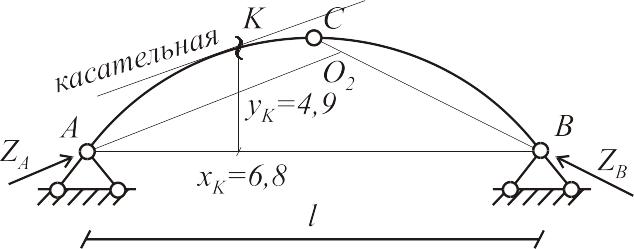
Рис.6.1 Построение линий влияния опорных реакций в арке.

так как единичная нагрузка вертикальна, то в этом случае опорные реакции и внутренние усилия в трехшарнирной арке выразятся через аналогичные усилия в простой балке того же пролета, что и арка (рис. 6.1 б). Из равенства вертикальных составляющих опорных реакций арки и балки ( и ) следует, что ЛВ вертикальных составляющих опорных реакций арки и совпадают соответственно с ЛВ опорных реакций простой балки и , рис.6.1 б, и определяются по формулам

;

.

Линии влияния показаны на рис.2.14 в и г. Величина распора при вертикальной нагрузке определяется по формуле

,где - изгибающий момент в сечении простой балки (под шарниром ); - высота арки.Из данного выражения следует, что для построения ЛВ распора достаточно построить ЛВ изгибающего момента в сечении простой балки и уменьшить ее ординаты в раз, т.е.

.

Таким образом, линия влияния представляет собой треугольник с вершиной под шарниром и с ординатой в вершине, равной (рис. 6.1 д).

Внутренние усилия , , в сечении арки при вертикальной нагрузке определяются по формулам:

;

;

.

Из этих формул следует, что ЛВ , , в арке могут быть построены алгебраическим сложением известных линий влияния изгибающего момента , поперечной силы в простой балке и распора , умноженных на соответствующие коэффициенты , , , т.е.

;

;

.

Результаты выполненных сложений в соответствии с данными формулами при показаны на рис.6.2 а-д, 6.3 в, 6.4 в.

Необходимо учитывать, что при расположении сечения в правой полуарке угол отрицателен, т.е. , . Для большей наглядности построенных линий влияния и удобства их использования можно развернуть данные ЛВ на горизонтальные оси. Для этого надо отложить ординаты результирующих линий влияния (рис.6.2 е, 6.3 г, 6.4 г) от одной прямой.

При переходе к горизонтальной оси в линии влияния неизменными остаются положение нулевой точки и ордината . Таким образом, ЛВ состоит из трех прямолинейных участков. При этом ЛВ можно построить в следующем порядке.

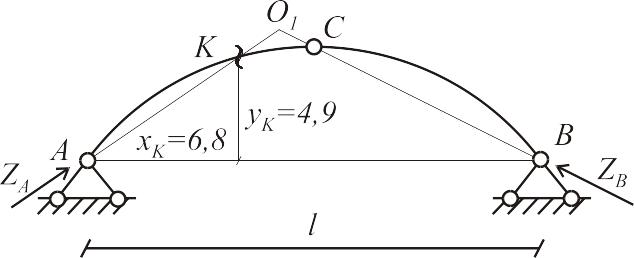
1.Определяется положение нулевой точки ; при размещении груза в ней изгибающий момент в сечении будет равен нулю. Это возможно в том случае, если линия действия левой опорной реакции проходит через точку , т.е. направлена по прямой . Поскольку груз находится на левой полуарке, а правая не загруженна, результирующая реакция опоры будет направлена вдоль прямой, соединяющей точки и . Таким образом, нулевая точка находится на пересечении двух прямых: и (рис. 6.2 а).

2.Над опорой откладывается ордината ; через нее и нулевую точку проводится прямая (рис. 6.2 д). На данную прямую сносятся сечение (точка ) и сечение (точка ). Соединяя последние с нулевыми точками под опорами и арки, получим окончательный вид ЛВ (рис. 6.2 д).

Контролем правильности построения ЛВ алгебраическим сложением (рис. 6.2 в-д) является равенство нулю ординаты ЛВ над нулевой точкой.

а
б
в
г
д
е

Рис.6.2. Построение линий влияния изгибающего момента в заданном сечении на оси арки.

Для построения ЛВ (рис. 6.3) на горизонтальной оси необходимо выполнить следующие действия.

а
б
в
г

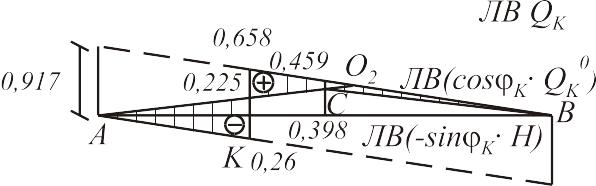
Рис.6.3. Построение линий влияния перерезывающей силы в заданном сечении на оси арки.

Над опорой откладывается ордината (рис. 6.3 в). Через нее и нулевую точку проводится прямая. При этом нулевая точка находится на пересечении прямой , вдоль которой направлена реакция . и линии , проходящей параллельно касательной, проведенной в сечении арки (рис. 6.3а). Для того чтобы при расположении груза в нулевой точке поперечная сила в сечении была равна нулю, реакция должна быть направлена так, чтобы ее проекция на нормаль к касательной (это и есть величина ) при рассмотрении равновесия левой полуарки была равна нулю, т.е. проходила вдоль линии, параллельной касательной.

Из точки проводится прямая, параллельная прямой .

На полученные прямые сносятся сечение (точки , ) и шарнир (точка ); последняя соединяется с нулевой ординатой над опорой , а через точки и проводится вертикальная прямая (рис. 6.3 г).

Нулевая точка продольной силы (рис. 6.4 а) лежит на пересечении линии действия реакции (прямая ) и линии действия реакции , которая должна быть направлена так, чтобы при положении груза в нулевой точке величина была равна нулю. Это возможно, если направлена перпендикулярно касательной, проведенной в сечении (только в этом случае сумма проекций всех сил рассматриваемой левой части арки на касательную, вдоль которой направлена , будет равна нулю). После определения нулевой точки порядок построения ЛВ следующий.

Под левой опорой арки (точка ) откладывается вниз ордината (рис. 6.4 в); через нее и нулевую точку , снесенную на горизонтальную ось, проводится прямая.

Из точки проводится прямая, параллельная построенной

а
б
в
г

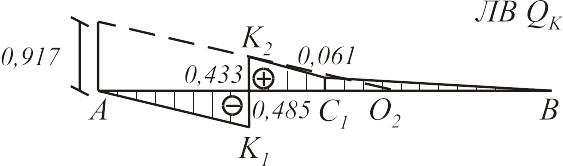
Рис.6.4. Построение линий влияния продольной силы в заданном сечении арки.

1. На полученные прямые сносятся сечение (точки и ) и шарнир (точка ), последняя соединяется с нулевой ординатой в точке ; точки и соединяются вертикальной прямой, а точки и - отрезком (рис. 6.4 г).

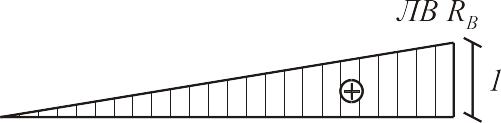
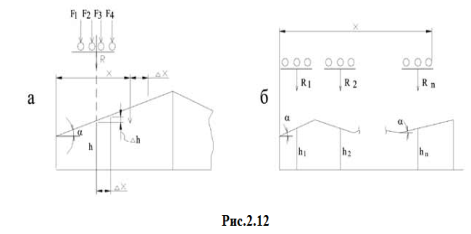
19.определение наиневыгоднейшего положения системы связанных сосредоточенных сил в случае полигональной линии влияния.

Такая нагрузка на сооружение возникает при движении по нему транспортных средств (поезд, автоколонна и так далее).Рассмотрим систему жестко связанных грузов (рис.2.12,а), положение которой характеризуется расстоянием x от начала линии влияния до первого груза. Пусть система грузов переместилась на ∆x , оставаясь полностью на участке ав. При этом равнодействующая также переместится на ∆x , а ордината под ней изменится на ∆h=∆x*tgα , следовательно, усилие S получит приращение ∆S=R*∆h=R*∆x*tgα

Когда загружены несколько участков линии влияния, можно нагрузку на каждом участке заменить равнодействующей (рис.2.12,б):

eсли нагрузка переместится на небольшое расстояние ∆x так, что грузы останутся на тех же участках, то равнодействующие не изменяются, а усилие S получит приращение (2.1)

и тогда (2.2)

В соответствии с (2.1) приращение усилия линейно зависит от ∆x до тех пор, пока ни один из грузов не перейдет через вершину, следовательно, график изменения усилия в зависимости от ∆x будет линейным (рис.2.13).

Из (2.2) и рис.2.13 следует:

Критерием достижения усилием максимального значения будет изменение знака выражения (2.2) при переезде грузов через одну из вершин линии влияния или обращение его в нуль, что соответствует горизонтальной линии на графике. Этот критерий позволяет определить только локальный максимум. Перебор же всех возможных вариантов вручную может быть достаточно трудоемким.

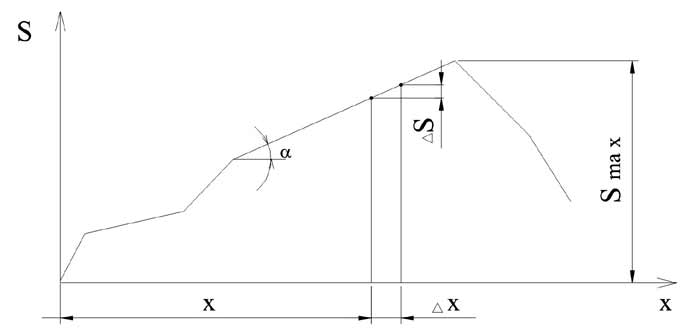
Рис.2.13

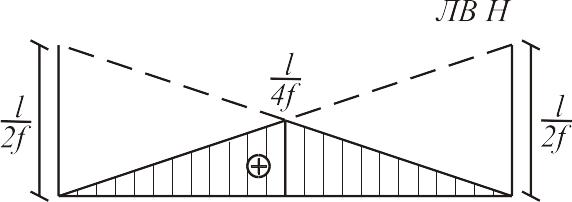
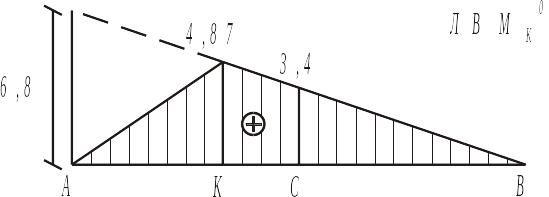
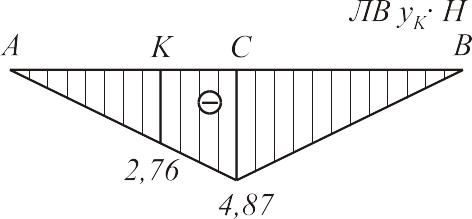
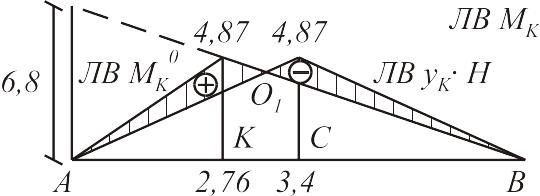
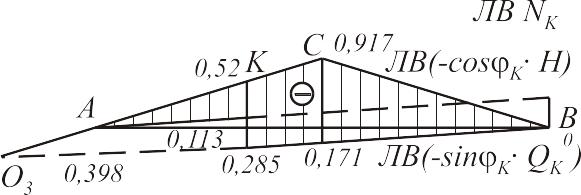
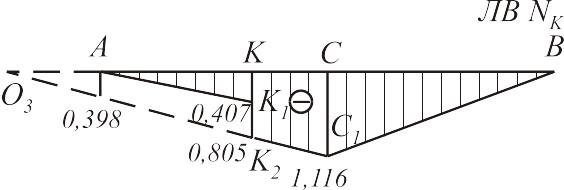
В практике расчетов чаще всего встречается загружение треугольной линии влияния (рис.2.14).

(2.4)

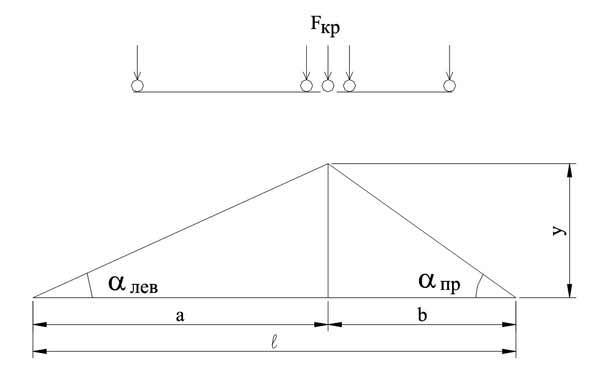
Рис. 2.14

Знак выражения (2.4) не зависит от у, поэтому задача сводится к определению того груза, переход которого через вершину линии влияния изменяет знак величины, стоящей в скобках выражения (2.4). Этот груз называется критическим. Очевидно, что при достижении грузом критического значения. Отсюда(2.5),(2.6)

Формулы (2.6) можно использовать только в том случае, когда система грузов полностью расположена над треугольной линией влияния.Ввиду того, что невыгодное положение нагрузки не зависит от размера ординаты y , можно для каждого вида подвижной нагрузки при различных l и a/l найти max при y=1 . Затем действие подвижной нагрузки при невыгодном ее расположении можно заменить действием нагрузки, равномерно распределенной по вcей длине l. Такая нагрузка называется эквивалентной. Ее интенсивность определим из условия(2.7)

Откуда

Эквивалентная нагрузка зависит от длины треугольной линии влияния, положения ее вершины, типа подвижной нагрузки и приводится в справочных таблицах.Максимально возможное усилие вычисляется через площадь линии влияния: