Прямоугольный треугольник

Прямоугольным называется сферический треугольник, у которого по меньшей мере один угол равен 90^о.

Если угол С – прямой, то противоположная сторона c – гипотенуза.

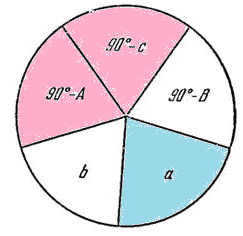
Соотношения между сторонами и углами прямоугольного сферического треугольника по правилу Непера:

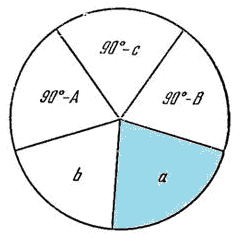
синус любого из углов, изображенных на диаграмме (например а), равен

1) произведению тангенсов двух углов, прилежащих к нему на диаграмме,

2) произведению косинусов двух углов, противолежащих ему на диаграмме.

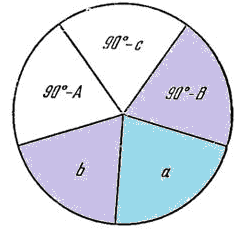
Пример 2.

Найти стороны и углы прямоугольного сферического треугольника, зная гипотенузу c и сторону a ( ).

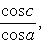
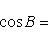
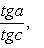
Если a меньше, равно или больше 90^о, то A соответственно меньше, равно или больше 90^о, и наоборот.

Если даны a и A, то задача имеет решение только в том случае, когда выполнено предыдущее условие и , причем если , то решений два.

Если даны A и B, задача имеет решение только при условий

и .

Сферический треугольник со стороной, равной 90^о, называется квадрантным треугольником. Это полярный треугольник к прямоугольному сферическому треугольнику.

Решение треугольников

a, b, c – стороны,

A, B, C – углы, противолежащие сторонам a, b, c.

r и ρ – радиусы описанного и вписанного конусов.

Формулы сферической тригонометрии:

1. Теорема косинусов для угла: Косинус угла равен минус произведению косинусов двух других углов плюс произведение синусов тех же углов на косинус стороны, лежащей между ними (т.е. противолежащей первому углу).

2. Теорема синусов: Во всяком сферическом треугольнике синусы сторон относятся как синусы противоположных им углов

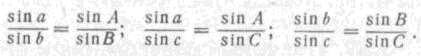
3. Теорема косинусов для стороны: Во всяком сферическом треугольнике косинус стороны равен произведению косинусов двух других сторон плюс произведение синусов тех же сторон, умноженное на косинус угла между ними (т.е. на косинус угла, противолежащего первой стороне).

4. Теорема котангенсов: Во всяком сферическом треугольнике произведение котангенса крайнего угла на синус среднего угла равно произведению котангенса крайней стороны на синус средней стороны минус произведение косинусов средних элементов.

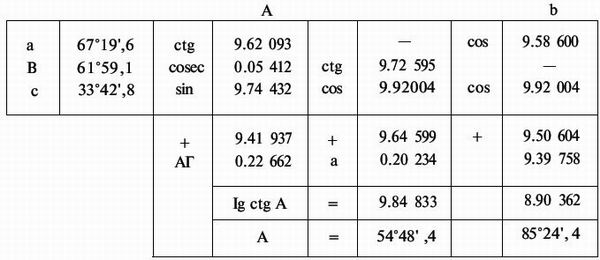
Пример.

Д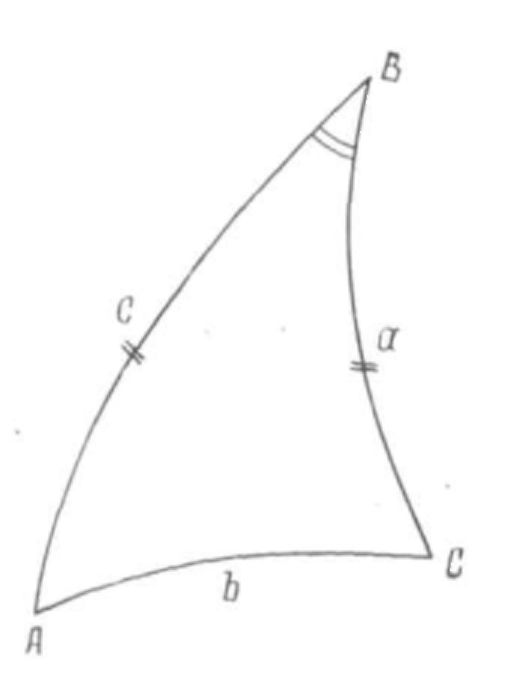 ано: а = 67°19',6, с=33°42',8 , В = 118°00',9.

Найти А, b, С. 

Решение.

1. Пользуясь сферическим треугольником, выписываем формулы, связывающие три известных элемента с искомым:

ctg Аsin В = ctg аsin с – cos с  cos В;

cos b = cos а  cos с + sin а  sin с  cos В;

ctg С  sin В = ctg с  sin а – cos a  cos В.

2. В полученных формулах анализируем знаки множителей:

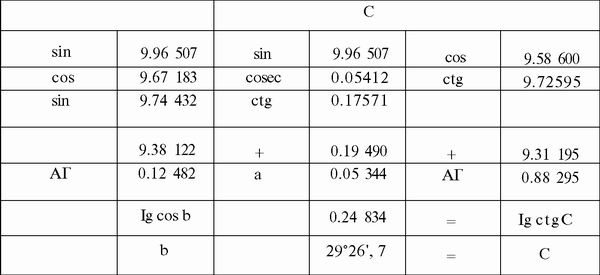
3. Выписываем рабочую схему и решаем задачу

Вычисление сторон и углов по заданным сторонам и/или углам:

(Формулы могут быть получены одновременной циклической перестановкой A, B, C и a, b, c).

 (теорема синусов),

 (теорема косинусов для сторон),

 (теорема косинусов для углов),

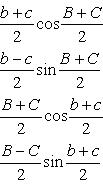
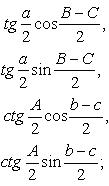
(пропорции (аналогии) Непера)

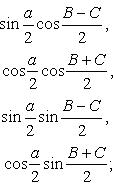
(пропорции Деламбра и Гаусса)

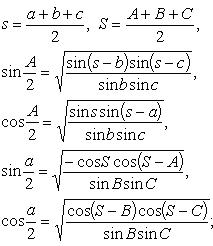
 (формулы половинных углов)

Таблица решения сферических треугольников

	Даны	Формулы для вычисления	Условия существования решения
1	Три стороны a, b,c	A, B, C из формул половинных углов и циклической перестановки	Сумма двух сторон должна быть больше третьей
2	Три угла A, B, C	a, b, c из формул половинных углов и циклической перестановки	Сумма двух сторон должна быть меньше   плюс третий угол
3	Две стороны и заключенный между ними угол b, c, A	и  из аналогий Непера, затем B и C;  из аналогий Деламбра и Гаусса, формул половинных углов или теоремы косинусов для сторон
4	Два угла и заключенная между ними сторона B, C, a	и  из аналогий Непера, затем b и c; A из аналогий Деламбра и Гаусса, формул половинных углов или теоремы косинусов для углов
5	Две стороны и противолежащий одной из них угол b, c, B	C из  теоремы синусов, A и a из аналогий Непера	Задача имеет одно или два решения, если . Сохраняются те из величин C, для которых A - B и a - b имеют одинаковый знак: и  также должны быть одного знака
6	Два угла и противолежащая одному из них сторона B, C, b	c из теоремы синусов, A и a из аналогий Непера	Задача имеет одно или два решения, если . Сохраняются те из величин c, для которых  A - B и a - b имеют одинаковый знак: и  также должны быть одного знака

16