Сферические треугольники

Основные понятия

Кратчайшее расстояние между двумя точками сферы измеряется вдоль окружности большого круга, т.е. окружности, плоскость которой проходит через центр шара.

Сферическая прямая – большая окружность, полученная сечением сферы плоскостью, проходящей через центр сферы.

Сферический отрезок АВ (расстояние между точками А и В) равно угловой величине a соответствующей дуги, если R=1.

Любая точка С сферического отрезка АВ разбивает его на два отрезка, сумма сферических длин которых равна длине всего отрезка как в планиметрии

ÐАОС + ÐСОВ = ÐАОВ

Задача 1

Докажите, что для любой точки D вне отрезка имеет место «сферическое неравенство треугольника»: сумма сферических расстояний от D до А и от D до В больше длины отрезка АВ, или

ÐАОD + ÐDОВ > ÐАОВ

Сферическим треугольником называется фигура на сфере, образованная тремя прямыми, не проходящими через общую точку, и тремя точками их попарного пересечения. (всего от трех прямых треугольников может быть восемь).

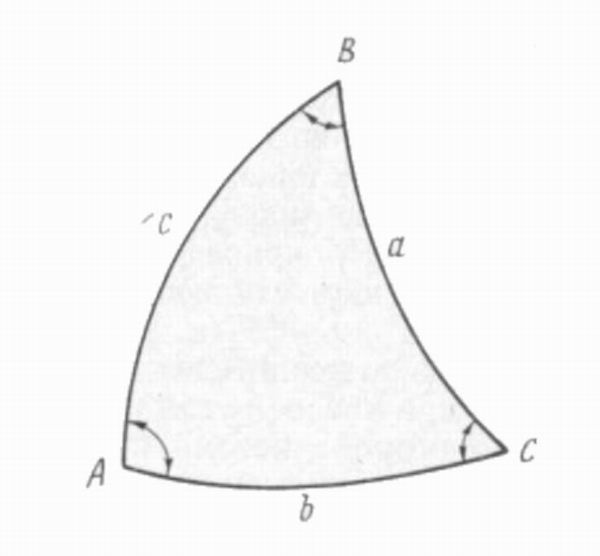
Вершины сферического треугольника являются точками пересечения трех лучей, выходящих из центра шара и сферической поверхности.

Стороны сферического треугольника – дуги больших окружностей, ограничивающие треугольник (или в тригонометрии центральные (плоские) углы, образованные радиусами, идущими к вершинам (меньшие 180^о, если один из этих углов 180^о, то треугольник вырождается в полуокружность большого круга). Каждой стороне треугольника соответствует дуга большого круга. Дугу принять за сторону сложно, т.к. ее трудно измерить).

Поэтому, решая задачи по учебному пособию, следует обращать внимание на определения основных понятий.

Углы сферического треугольника – углы между сторонами – дугами в вершинах треугольника (или линейные углы двугранных углов, образованных плоскостями больших окружностей, или углы между дугами больших окружностей, которые измеряются как углы между касательными в соответствующих вершинах).

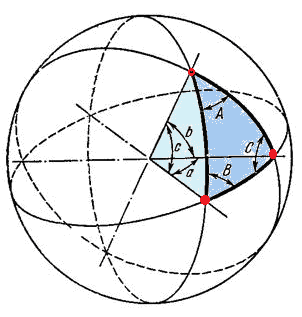
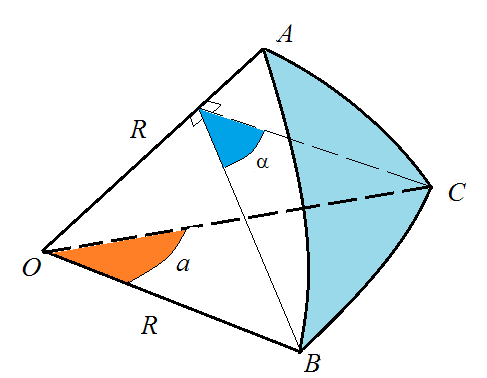
Сферический треугольник АВС (второй вариант определения):

a, b, c – стороны (центральные углы граней),

А, В, С: – вершины,

, ,  – углы (двугранные углы между гранями).

Каждому сферическому треугольнику соответствует трехгранный угол с вершиной в центре сферы, что позволяет выполнять доказательства для сферических объектов, используя евклидову планиметрию и стереометрию.

Свойства сферических треугольников

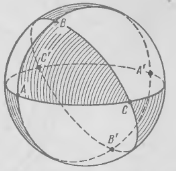
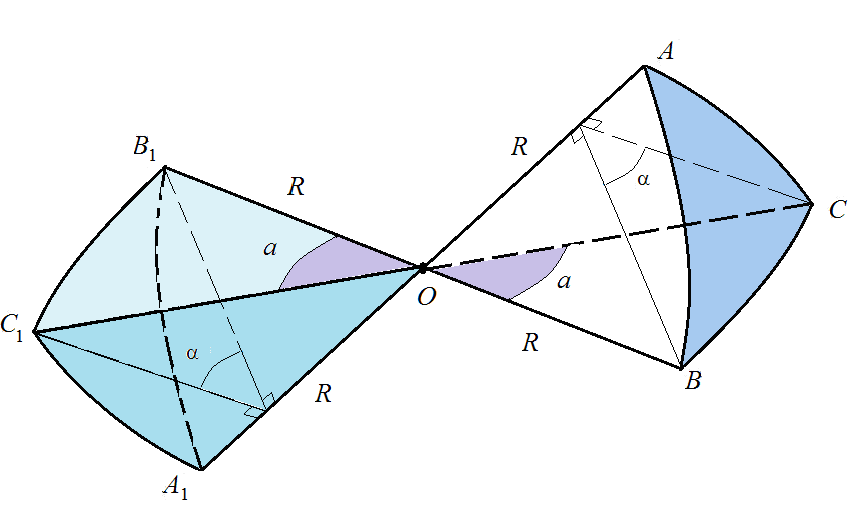
Всего от трех прямых треугольников может быть образовано 8 треугольников, из них три имеют с данным общую дугу и грань (А₁ВС, АВС₁, АВ₁С), где А₁, В₁, С₁ – точки, диаметрально противоположные точкам А, В, С.

Треугольники, имеющее с данным треугольником АВС общую дугу, называют смежными с ним. Углы, прилегающие к общей стороне, дополняют соседние углы треугольника до 180^о.

Треугольники АВС и А₁В₁С₁ называют симметричными (соответственными).

Симметричные треугольники попарно равновелики. Однако их нельзя считать равными (конгруэнтными), т.к. нельзя наложить один на другой перемещением (с учетом их выпуклости).

Площадь сферического двуугольника и треугольника

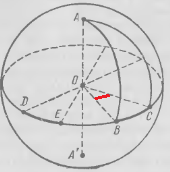
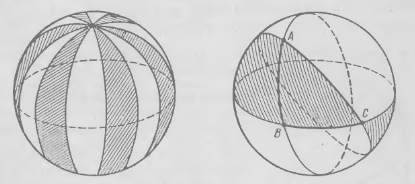
Площадь сферы (угол 2): .

Площадь двуугольника с углом в 1 радиан:

Площадь двуугольника с углом  радиан:

Пример.

Вычислите площадь двуугольника с углом, равным 30^о, на сфере, радиус которой 5 см.

Решение. (радиан)

(кв.см)

или

(кв.см).

Расчет:

2	5	30	0,523599
0,30103	0,69897		-0,281		1,417969	сумма логарифмов
					26,17994	степень 10

Сферический треугольник получается из двуугольника делением третьей сферической прямой. Каждая пара их трех определяет 6 двуугольников: два с вершиной (углом) А, два – с В, два – с С. Тогда сумма площадей двуугольников равна сумме площадей всей сферы и четырех площадей треугольника АВС:

где А, В, С – углы сферического треугольника.

Следствие 1.

. Значит, , т.е.

.

Сумма углов сферического треугольника больше 180^о.

Величина называется угловым избытком (эксцессом) треугольника и измеряется в радианах.

Величина называется дефектом треугольника.

Следствие 2.

Избыток угла сферического треугольника прямо пропорционален его площади и обратно пропорционален квадрату радиуса сферы.

Наибольшим треугольником считается тот, для которого

Дл этого треугольника: избыток равен 2, сумма углов 3.

Если , то избыток стремится к нулю, сумма углов к 180^о, сфера к евклидовой плоскости. Значит, евклидова плоскость – предельный случай сферической геометрии.

Пример.

Вычислите площадь треугольника с углами, равными 30^о, 120^о и 60^о на сфере, радиус которой 5 см.

Решение.

(радиан)

(кв.см)

или ,

(кв.см).

Расчет:

5	30	0,523599
0,69897		-0,281		1,116939	сумма логарифмов
				13,08997	степень 10