Диаграмма состояний

Рассмотрим регулярную диаграмму G[z] :

Z::= V0|V1

U::= Z1|1

V::= Z0|0

Порождённый ею язык состоит из последовательностей образуемых парами 01 или 10, т.е. L(G) = {B |n>0}, где В ={01, 10}.

Чтобы облегчить распознавание предложений грамматики G нарисуем диаграмму состояний.

Рис.6.

В этой диаграмме каждый нетерминал грамматики G представлен узлом или состоянием. Кроме того, есть начальное состояние S ( предполагается, что грамматика не содержит нетерминала S).

Каждому правилу Q::=T соответствует дуга с пометкой Т, направленная от начального состояний S к состоянию Q. каждому правилу Q::=КТ соответствует дуга с пометкой Т, направленная от состояния К к состоянию Q.

Диаграммы состояний используются, чтобы распознать или разработать цепочку Х следующим образом:

1. Первым текущем состоянием считать S. Начать с самой левой литеры в цепочке Х и повторить шаг 2 тех пор, пока не будет достигнут конец Х.

2. Сканировать следующую литеру Х, продвинуться по дуге, помеченной этой литерой, переходя к следующему текущему состоянию.

Если при каком-то повторении шага 2 такой дуги не оказывается, то цепочка Х – не является предложением языка и происходит остановка. Если мы достигнем конца Х, то Х предложение когда последнее текущее состояние есть Z.

На каждом шаге, кроме первого, основой является имя текущего состояния, за которым следует входной символ. Символ, к каждому приводится основа, будет именем следующего состояния.

Пример:

ШАГ ТЕКУЩЕЕ СОСТОЯНИЕ ОСТАТОК ЦЕПОЧКИ

Z

1 S 101001 V |

2 U 010001 Z | |

3 Z 1001 U | | |

4 U 001 Z | | | |

5 Z 01 U | | | | |

6 V 1 1 0 1 0 0 1

7 Z

Рис.7.

Каждая строка отражает состояние разбора перед началом выполнения шага 2.

В этом примере разбор выглядит столь простым благодаря характеру правил, т.к. нетерминалы встречаются лишь как первые символы правой части. На первом шаге первый символ предложения всегда приводится к нетерминалу. На каждом последующем шаге первые два символа VT синтециальной формыVTt приводится к нетерминалу U, при этом используется правило U::=VT. При выполнении этой редукции имя текущего состояния U, а имя следующего текущего состояния V. Т.к. каждая правая часть единственна, то единственным оказывается U символ, к которому она приводится.

Синтаксические деревья для предложений регулярных грамматик всегда имеют вид, подобный изображённому.

Чтобы избавится от проверки на каждом шаге, есть ли дуга с соответствующей пометкой, можно добавить ещё одно состояние F(неудача) и добавить все необходимые дуги от всех состояний к F. Добавляется также дуга, помеченная всеми возможными литерами ведущая из F обратно в F. В результате диаграмма имеет вид:

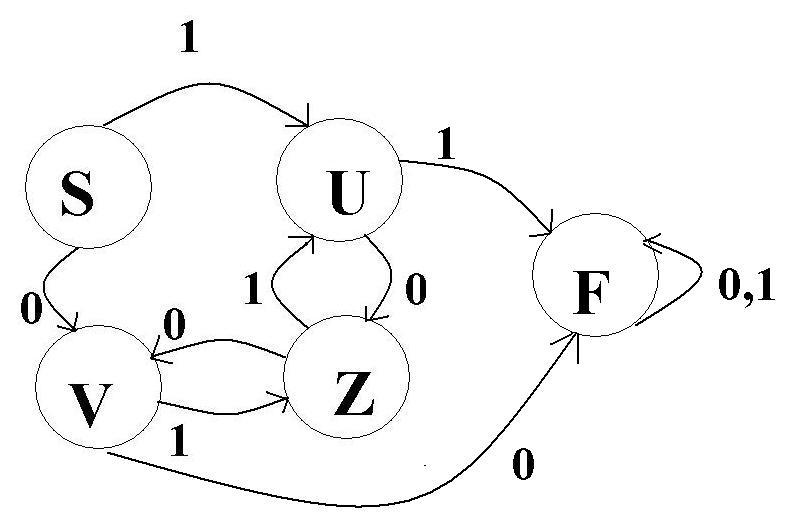
Рис.8.

Определение 13:

Детерминированный автомат с конечным числом состояний (КА) – это пятёрка (K, VT, M, S, Z),

K- алфавит элементов, называемых состояниями;

VT – алфавит, называемый входным алфавитом( литеры, которые могут встретится в цепочке или предложении);

М – отображение (или функция) множества К VT во множество К (если M(Q,T)=R, то это означает, что из состояния Q при входной литере Т происходит переключение в состояние R);

S К - начальное состояние;

Z – непустое множество заключительных состояний, каждое из которых К.

Можем так же формально определить, как работает КА с входной цепочкой t. Сделаем это расширив, понятие отображение, которое указывает, как переключаются состояния в зависимости от входной литеры.

Определим:

М(Q,λ)=Q при любом состоянии Q

M(Q, Tt) = M(M(Q,T), t) для любых t VT* u любыхT VT.

Первая строка означает, что если на входе пустой символ, то состояние остаётся прежним. Вторая строка показывает, что в состоянии Q и при входной цепочке Tt мы применяем М, чтобы перейти в состояние Р=M(Q, T), а затем применяем отображение M(P,t). Конечный автомат (КА) допускает цепочку (цепочка считается допустимой), если M(S,t)=P, где состояние Р принадлежит множеству заключительных состояний Z.

Такие автоматы называются детерминированными, т.к. на каждом шаге входная литера однозначно определяет следующее текущие состояние.

Рассмотренной диаграмме состояний соответствует следующий КА:

КА ({S, Z, U, V, F}, {0, 1}, M, S, {Z}), где

M(S,0)=V M(S,1)=U

M(V,0)=F M(V,1)=Z

M(U,0)=Z M(U,1)=F

M(Z,0)=V M(Z,1)=U

M(F,0)=F M(F,1)=F

Мы рассмотрели регулярную грамматику, которая имела единственные правые части. Для неё мы смогли построить диаграмму состояний. Эта диаграмма фактически была неформальным представлением КА. Легко видеть, что если предложения х принадлежит грамматике G, то оно также допускается КА, соответствующим грамматике G.

Определение14:

Регулярным множеством называется множество цепочек, которое распознаётся некоторым конечным распознавателем.