§ II.1.3. Равновесное, состояние решетки

Помимо сил химической связи, притягивающих атомы, между атомами действуют силы отталкивания, обусловленные взаимодействием внутренних электронных оболочек или ядер. Обе эти силы зависят от расстояния. Однако силы притяжения являются дальнодействующими и возрастают сравнительно медленно с уменьшением расстояния между атомами, в то время как силы отталкивания являются короткодействующими и очень резко возрастают при уменьшений расстояния.

Современная теория дает приближенную формулу для силы притяжения:

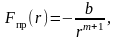
где b и m — постоянные, зависящие от вида химической связи. Так, например, в ионных кристаллах и в металлах m = 1, а в кристаллах с молекулярной связью m = 6. Силы притяжения и соответствующая им потенциальная энергия обычно записываются с отрицательным знаком.

Силы отталкивания выражаются сложной математической зависимостью от расстояния. В грубом приближении они могут быть описаны формулой

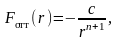
где с и n — постоянные, зависящие от природы атомов. Для некоторых кристаллов обычно полагают n = 12.

При определенном расстоянии, между атомами r == а эти силы уравновешивают друг друга, в результате чего атомы оказываются в равновесном состоянии.

Перейдем к рассмотрению энергии, обусловленной силами притяжения и отталкивания. Поскольку составляющие потенциальной энергии взаимодействия атомов будут иметь вид:

где В = b/m, С = c/n. Тогда результирующую потенциальную энергию запишем как

На рис. 1.7 показаны составляющие потенциальной энергии, а также-результирующая энергия Е взаимодействия атомов. Здесь энергия свободных атомов принята за нуль.

Как видно из рисунка, равновесному состоянию атомов, когда F = 0, соответствует минимальное отрицательное значение потенциальной энергии Е_о. Следовательно, равновесное состояние является устойчивым. При всяком малом отклонении атомы возвращаются в исходное состояние.

Следует отметить, что приведенное рассмотрение равновесного состояния весьма упрощено. Фактически атомы в кристаллической решетке испытывают значительно большее число взаимодействий. Наиболее важным из них является влияние атомов, окружающих, данную пару. Если даже рассматривать линейную цепочку атомов, то уже очевидно, что на данную пару действуют силы взаимодействия с соседними атомами, которые в свою очередь связаны с последующими атомами, и т.д. В трехмерных кристаллических решетках картина резко усложняется. Задача отыскания условия равновесного состояния атомов в кристаллической решетке существенно усложняется и является по сути дела задачей многих тел. Однако, несмотря на это, качественная картина равновесного устойчивого состояния атомов в кристаллической решетке остается той же.

В реальных кристаллических решетках атомы практически никогда не находятся в положении устойчивого равновесия, так как они непрерывно совершают колебательные движения вокруг этого устойчивого состояния. Даже при абсолютном нуле температуры, атомы совершают так называемые нулевые колебания и обладают некоторой конечной «нулевой» кинетической энергией.

При повышении температуры интенсивность колебаний атомов вокруг устойчивого состояния увеличивается. При дальнейшем повышении температуры возможен случай, когда энергия теплового колебательного движения превысит энергию связи частиц Е₀. В этом случае, очевидно, частица не возвратится в исходное состояние, и химическая связь будет разорвана.

Многие элементы и химические соединения в силу сложной структуры электронных оболочек и кристаллической решетки могут иметь, не один, а два и более минимумов энергии, причем последовательность этих; минимумов может располагаться не только в радиальных направлениях, но и по угловым координатам. Каждый минимум энергии соответствует определенному виду кристаллической решетки. В этом случае элемент или соединение кристаллизуется в такой решетке, которая соответствует наиболее глубокому минимуму энергии. При определённых температурных условиях может произойти перестройка кристаллической структуры, сопровождающаяся переходом в другой минимум потенциальной энергии. Способность к перестройке кристаллической решетки у некоторых веществ получила название полиморфизма. Наличие последовательности минимумов энергий в определенных предпочтительных направлениях свидетельствует об анизотропии сил межатомного взаимодействия. В результате такой перестройки возникают структурные модификации одного и того же, элемента или соединения. Примером таких модификаций является серое и белое олово, алмаз и графит.

Тепловые колебания решетки. Фононы

Под влиянием какого-либо воздействия атом, выведенный из равновесия совершает колебательные движения вокруг этого равновесного состояния. Так как все атомы кристаллической решетки связаны друг с другом упругими силами химической связи, то первичное возбуждение вызывает сложные движения соседних атомов. В связи с тем, что аналитическое описание этих движений является крайне сложным, обычно рассматривают упрощенную модель колебаний атомов. Например, предполагают, что силы, взаимодействия между атомами являются линейными, т.е. пропорциональны величине, смещения атома относительно равновесного положения. Это позволяет уравнение движения, каждого атома записать в сравнительно простой форме. Однако это упрощение еще не дает возможности разрешить задачу, так как в этом случае необходимо решить 3N взаимосвязанных уравнения движения, где N — число атомов в кристалле, а коэффициент 3 учитывает число возможных степеней свободы-каждого атома. Поэтому вместо изучения индивидуальных движений каждого атома рассматривают коллективные колебания всего ансамбля атомов. Поскольку кристаллическая решетка является симметричной, а силы химической связи являются упругими, коллективные колебания атомов представляют собой упругие волны, распространяющиеся во всевозможных направлениях по кристаллу.

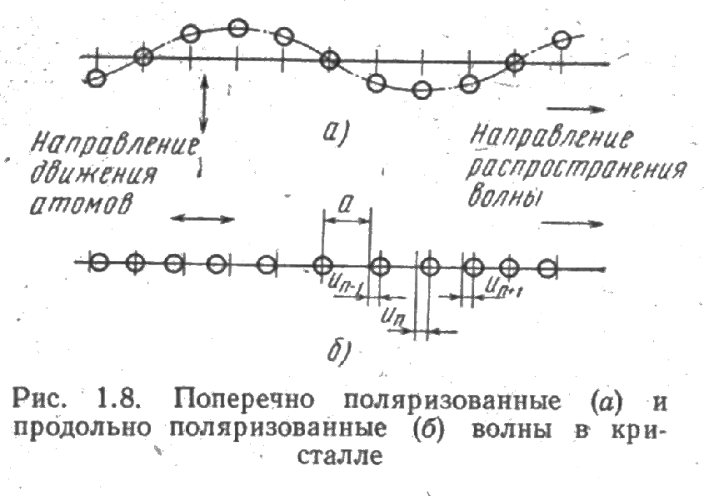
Колебания решетки отличаются друг от друга не только направлением распространения, но и длиной волны, сдвигом фазы соседних атомов и поляризацией. Наиболее коротковолновые колебания имеют длину волны равную удвоенному расстоянию между соседними атомами: λ_min=2a, а наиболее длинные – длину волны, равную удвоенной длине кристалла λ_max=2L. Для каждого направления распространения колебания в общем случае существует две поперечно поляризованные волны и одна продольно поляризованная. Поперечно поляризованные волны характеризуются колебаниями атомов в направлениях, перпендикулярных направлению распространения волны (рис. 1.8, а). В случае продольно поляризованных волн направление колебания атомов совпадает с направлением распространения влны (рис, 1.8,).

В теории колебаний волновой процесс принято характеризовать волновым вектором k, круговой частотой колебаний ω, фазовой и групповой скоростями распространения волны. Абсолютная величина волнового вектора

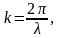(1.1)

а направление совпадает с направлением распространения волны. Фазовая скорость относится лишь к монохроматической волне и представляет собой скорость перемещения, в пространстве точки с заданной фазой. Фазовая скорость выражается следующей форулой:

(1.2)

В общем случае частота колебаний в кристалле, а также фазовая скорость имеют сложную зависимость от длины волны. Поэтому импульс, т. е. набор волн (волновой пакет), распространяется в пространстве с так называемой групповой скоростью, которая определяется формулой

(1.3)

Рассмотрим аналитическую зависимость частоты и скорости распространения волны в одномерном кристалле от ее длины или соответственно от волнового вектора k. Будем считать, что колебания атома вокруг равновесного состояния малы (см. рис. 1.8,б); зависимость энергии взаимодействия атомов от расстояния Е(r) вблизи равновесного положения описывается квадратичным законом, а силы, стремящиеся возвратить атом в исходное состояние, являются линейными. При расчете будем учитывать лишь взаимодействие данного атома с двумя ближайшими соседними, атомами. Сила, действующая на n-й атом, при этих условиях будет равна

где u – смещение атома из положения равновесия, f - коэффициент упругой силы. В соответствии со вторым законом Ньютона уравнение движения n-го атома принимает вид

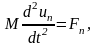(1.4)

где M – масса атома, t – время. Решением этого уравнения являются функции вида

(1.5)

представляющие собой уравнения бегущих волн. Здесь A_i — амплитуда i-ой волны, х_n = аn — координата n-го атома в цепочке. Подставляя это решение в (1.4), получим выражение для зависимости ω(k):

(1.6)

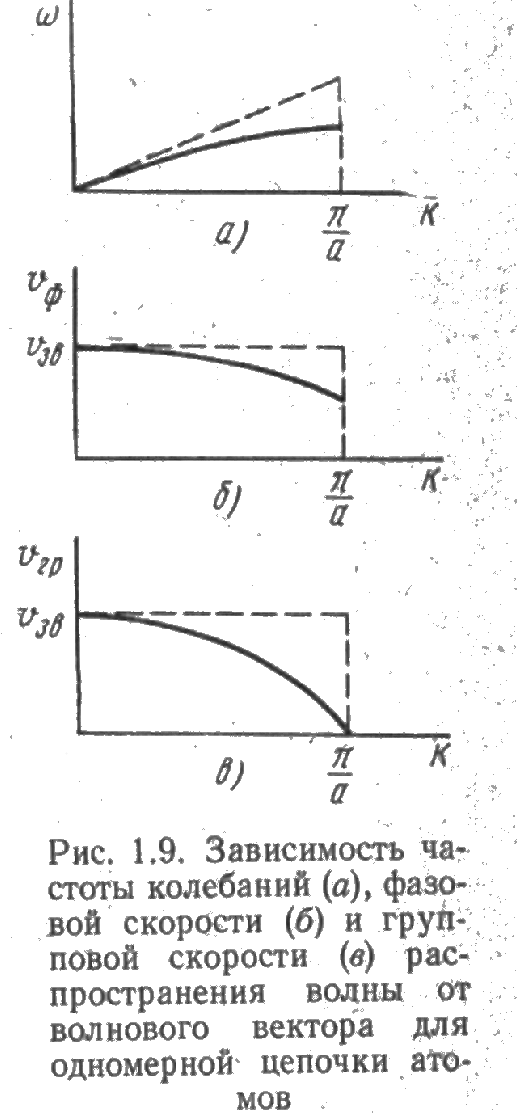
C учетом зависимостей (1.2) и (1.3) найдем выражения для фазовой и групповой скоростей:

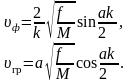
На рис. 1.9 приведены графики полученных зависимостей. Нетрудно видеть, что при k→0, т. е. в случае длинных волн, групповая и фазовая скорости обращаются в постоянную величину, равную скорости распространения звука υ_зв в кристалле:

(1.9)

Для самых, коротких волн, соответствующих к = π/a, групповая скорость стремится к нулю, а фазовая скорость — к величине В случае длинных волн кристалл можно рассматривать как непрерывную среду, скорость распространения упругих колебаний в которой максимальна и равна скорости звука. Если бы кристалл по своей структуре представлял непрерывную упругую среду, то зависимость ω(к) выродилась бы в прямую линию, а групповая и фазовая скорости были бы постоянны и равны скорости звука, как это показано на |рис. 1.9 штриховыми линиями. Однако на коротких волнах кристаллическую решетку уже нельзя рассматривать как непрерывную среду. Тот факт, что масса колеблющейся системы сосредоточена в отдельных точках, вносит существенные изменения в процесс колебания. Это сосредоточение оказывается эквивалентным увеличению массы системы или ее инерционности. В свою очередь увеличение инерционности приводит к снижению частоты и скорости распространения коротких волн.

Произведем ориентировочную оценку, спектра частот колебаний атомов и сопоставим его с диапазоном звуковых волн. При постоянной решетке порядка 3 10^-8 см^-1 максимальный волновой вектор равен к_max = 10⁸ см^-1. Полагая скорость звука равной υ_зв = 10⁵ см/сек, из (1.6) получим максимальную частоту 10¹² гц. Таким образом, звуковые волны представляют ничтожную часть спектра колебаний атомов твердого тела.

Следует заметить, что при выводе формулы (1.6) размеры кристалла не ограничивались, в результате чего спектр разрешенных значений частот ω колебаний является непрерывным. Однако в случае ограниченного кристалла с, конечным числом атомов N, как показывает анализ [2], спектр частот колебаний является дискретным, причем общее число разрешенных значений частот или соответственно число колебаний равно 3N. Эта величина совпадает с числом степеней свободы атомов в кристалле.

В кристаллах, состоящих из двух видов атомов с различной массой либо с одинаковой массой, но с различными расстояниями между атомами, а также в сложных решетках наблюдаются две ветви у зависимости частоты колебаний от волнового, вектора. На рис. 1.10 представлены кривые зависимости ω(к) для этого случая. Очевидно, каждой длине волны соответствуют два вида колебаний с существенно различающимися частотами. Колебания, описываемые верхней ветвью называются оптическими, а нижней — акустическими. Как уже было сказано выше, появление двух ветвей частот колебаний атомов кристалла обусловлено либо различием в их массах, либо различием коэффициентов упругой связи между атомами. Так, в случае одномерной решетки, составленной из двух типов атомов, существование двух частот колебаний, соответствующих одному значению длины волны, в области коротких воли объясняется колебаниями тяжелых атомов при покоящихся легких атомах и наоборот, как это показано на рис, 1.11, а. Очевидно, колебания более легких атомов дают более высокую частоту при одной и той же длине волны. При больших длинах волн акустическая ветвь образуется в результате колебаний всей цепочки, как и в случае одноатомной решетки (рис. 1.11, б), а оптическая ветвь обусловлена встречными колебаниями соседних атомов внутри элементарной ячейки решетки (рис. 1.11, в). В пределе при λ→∞ оптическая ветвь обусловлена тем, что все атомы колеблются в одной и той же фазе и с одинаковой амплитудой, как показано на рис. 1,11, г.

Рис. 1.10. Оптическая (а) и акустическая (б) ветви зависимости частоты колебаний от волнового вектора

Колебания атомов в трехмерной кристаллической решетке представляются более сложными. В кристаллах с одним атомом в элементарной ячейке существуют только акустические колебания: При этом каждому заданному по величине и направлению волновому вектору соответствуют три колебания: одно продольное и два поперечных. При постоянных амплитуде и длине волны возвращающая упругая сила при продольных колебаниях больше, чем при поперечных. Это связано с тем, что продольные колебания вызывают сжатие и растяжение, а поперечные — только сдвиг. Поэтому частота и скорость поперечных колебаний меньше, чем продольных. В анизотропных средах частота и скорость распространения волны зависят не только от величины волнового вектора, но и от его направления.

Рис. 1.11. Колебания двухатомной цепочки: а) λ= 2а; б) акустические колебания, λ>>а; в) оптические колебания, λ>>а; г) оптические колебания, λ= ∞

В более сложных кристаллах, в элементарной ячейке которых содержится m атомов, кроме трех ветвей акустических колебаний, имеются 3(m— 1) оптических ветви, соответствующих внутриячеечным колебаниям.

Рассмотрим тепловые колебания кристаллической решетки в энергетическом аспекте. Расчет энергии каждого из 3N колебаний показывает, что эта энергия квантована. Допустимые значения энергии определяются формулой

, (1.10)

где n = 1,2, … , h -постоянная Планка, ν = ω/2π —частота колебания. Минимальной порцией, или квантом энергии колебаний, является ε = hν. Таким образом, упругие колебания кристаллической решетки квантованы. Подобно тому, как квантование электромагнитного излучения привело к представлению о фотонах, квантование упругих волн приводит к представлению об упругих колебаниях, как о системе фононов. Поэтому поле упругих колебаний решетки можно рассматривать как совокупность фононов.

Поскольку каждый фонон с частотой ν имеет свою энергию hν, то систему фононов можно рассматривать распределенной по энергетическому спектру. Кроме того, так как количество фононов и их частотный спектр изменяются с изменением температуры, то кривая распределения должна зависеть от температуры. Ш. Бозе и А. Эйнштейн показали, что частицы, подобные фононам, распределяются по энергиям по закону

(1.11)

где f(ν,T) - плотность вероятности обнаружения фонона с энергией ε = hν, k — постоянная Больцмана, а T — абсолютная температура. С этой точки зрения энергия тепловых колебаний кристалла представляет собой полную энергию фононов, которая может быть определена интегрированием по всему частотному спектру:

(1.12)

где g(ν)dν — число, тепловых колебаний в интервале частот dν. При низких температурах, когда спектр фононов охватывает лишь диапазон низких частот, верхний предел интегрирования может быть заменен на бесконечность. В этом случае интеграл (1.12) дает выражение для энергии кристалла

(1.13)

где N - число атомов в кристалле а θ — температура Дебая, определяемая из условия hν_max = kθ. Приведенная формула аналогична закону Стефана — Больцмана для плотности энергии излучения черного тела. Однако при высоких температурах эта формула неприменима, так как в отличие от фотонов спектр фононов ограничен в области высоких частот. В области высоких температур удельная энергия кристалла пропорциональна лишь первой степени температуры:

E = 3NkT. (1.14)

На рис. 1.12 иллюстрируется зависимость энергии кристалла от температуры. Сильная разница в характере зависимости Е(Т) в области высоких и низких температур обусловлена следующими причинами. При низких температурах энергия кристалла сильно возрастает за счет увеличения числа возбужденных колебаний. Так как спектр разрешенных колебаний в кристалле ограничен, а их полное число составляет 3N, то при некоторой температуре наступит такой момент, когда практически всё 3N колебаний будут возбуждены. Поэтому дальнейшее повышение энергии с ростом температуры возможно только лишь за счет увеличения энергии каждого колебания. По указанным причинам изменяется и характер зависимости числа фононов в кристаллах.

Если при низких температурах число фононов с ростом Т резко увеличивается

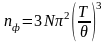(1.15)

благодаря расширению занимаемого фононами спектра частот, то при высоких температурах, когда весь частотный спектр занят, увеличение числа фононов происходит по формуле

(116)

лишь за счет увеличения их количества в данном типе колебаний.

Рис. 1.12. Зависимость энергии кристалла от температуры

Следует отметить, что приведенные формулы для энергии кристалла и концентрации фононов относились к случаю одноатомного кристалла. Для кристаллов, содержащих несколько типов атомов в элементарной ячейке, расчет энергии резко усложняется. В этом случае необходимо, очевидно, интегрировать по трем ветвям акустических колебаний и 3(m-1) ветвям оптических колебании.

Резюме

1. Атомы в кристаллах инертных газов связаны между собой силами Ван-дер-Ваальса (наведенное диполь-дипольное взаимодействие), которые изменяются с расстоянием R обратно пропорционально R⁶.

2. Возникновение сил отталкивания между атомами вызывается обычно тремя причинами:

а) увеличением кинетической энергии наиболее удаленных от ядра электронов, что является следствием сферической локализации электронного заряда в атоме;

б) электростатическим отталкиванием перекрывающихся электронных облаков и

в) принципом Паули, в силу которого электроны перекрывающихся электронных оболочек, имеющие параллельные спины, переходит ни уровни с более высокой энергией.

3. Ионы образуют ионные кристаллы за счет электростатического притяжения ионов разного знака. Энергия электростатического взаимодействия в структуре, состоящей из 2N ионов с зарядами ±q равна

где α — постоянная Маделунга, а R — расстояние между ближайшими соседями.

4. Связь между атомами в металлах в значительной степени обусловлена уменьшением кинетической энергии валентных электронов в металле по сравнению с кинетической энергией электронов в свободном атоме.

5. Ковалентная связь характеризуется перекрытием электронных оболочек атомов и участием в образовании связи электронов с антипараллельными спинами. Вклад во взаимодействие отталкивания, обусловленный действием принципа Паули, уменьшается для электронов с антипараллельными спинами, что делает возможным большую степень перекрытия электронных оболочек. Электроны перекрывающихся электронных оболочек связывают ионные остовы посредством электростатического притяжения.

Задачи:

1. Вычислить энергию электростатического взаимодействия ионов Na⁺ и Сl^-, расположенных на расстоянии 0,25 нм. По спектроскопическим экспериментальным данным энергия взаимодействия ионов Na⁺ и Сl^- равна 5,7 эв. Сравнить с результатом расчета.

2. Объяснить характер результирующей энергии взаимодействия Е атомов. Чем характеризуется взаимодействие при r = а?

3. Что такое полиморфизм.

4. Фононы – это квантовые эквиваленты звуковых волн в кристалле.

5. Ионные радиусы.

а) Сравнить ионные радиусы Захариазена из табл. 3.8 (Китель??) с опытными значениями постоянных решетки для кристаллов CsCl, NaCl и KBr.

б) Сравнить тетраэдрические радиусы со значениями постоянных решетки CuF, ZnS и InSb.

Примечание: Постоянные решеток указанных кристаллов даны в гл. I. (Китель??)

6. Линейный ионный кристалл. Рассмотреть цепочку 2N ионов с зарядами противоположного знака ±q. Считать, что потенциальная энергия отталкивания для ближайших соседей равна A/Rⁿ.

а) Показать, что в состоянии равновесия

б) Предположим, что кристалл сжимается таким образом, что R₀→R₀(1 — δ). Показать, что в выражение для работы, затрачиваемой на сжатие кристалла (работу отнести к единице длины), входит член Сδ²/2, где

Записать полученные результаты в системе СИ, заменив q² на q²/4πε₀. Примечание: Мы не можем получить этот результат, используя выражение для U(R_о), а должны использовать общее выражение для U(R).

7. Кубическая структура ZnS. Используя значения λ и ρ из табл. 3.5 (Китель??) и постоянные Маделунга, приведенные в тексте, рассчитать энергию связи для кристалла KCl с кубической структурой ZnS, описанной в гл. 1(Китель??). Сравнить полученный результат с величиной энергии связи, рассчитанной для кристалла KCl, имеющего структуру NaCl.

8. Модуль упругости LiF. Рассчитать модуль упругости кристалла LiF используя экспериментальные величины энергии связи и расстояния между ближайшими соседями. Сравнить результат с экспериментальным значением модуля упругости.

9. Водородные связи в кристаллах льда. Что является доказательством существования водородных связей в кристаллах льда? (См. книгу Полинга [33] и очень хорошую статью Ранелса «Лед» [41].). (Китель??)