§ II.5.2. Механизмы рассеяния и подвижность свободных носителей заряда

Полученные в предыдущем параграфе формулы для электропроводности в зависимости от времени релаксации не могут быть использованы, пока не будет установлена конкретная зависимость времени релаксации от энергии τ(Е) и произведено соответствующее усреднение. В свою очередь характер зависимости времени релаксации от энергии существенным образом зависит от конкретного механизма рассеяния. Центры рассеяния, т. е. объекты, с которыми могут взаимодействовать (соударяться) свободные носители заряда, могут иметь самую различную природу. Соответственно в реальном кристалле насчитывается сравнительно много различных механизмов рассеяния свободных носителей, каждый из которых дает свою зависимость τ(Е). Наиболее существенными механизмами: рассеяния являются: рассеяние на тепловых колебаниях решетки, на ионизированных и нейтральных атомах примеси, рассеяние на дислокациях, рассеяние в результате электрон-электронного взаимодействия и другие. Результирующее время релаксации и соответствующая подвижность носителей определяются совокупным действием указанных механизмов рассеяния.

Неравновесные носители заряда в полупроводниках

Образование, свободных носителей заряда в полупроводниках связано с переходом электронов из валентной зоны в зону проводимости. Для осуществления такого перехода электрон должен получить энергию, достаточную для преодоления запрещенной зоны. Эту энергию электрон получает от ионов решетки, совершающих тепловые колебания. Таким образом, преодоление запрещенной зоны электроном происходит обычно за счет тепловой энергии решетки. Концентрация носителей заряда, вызванная термическим возбуждением в состоянии теплового равновесия, называется равновесной.

Генерация и рекомбинация неравновесных носителей заряда

Однако, помимо теплового возбуждения, появление свободных носителей заряда может быть связано с другими причинами, например, в результате облучения фотонами или частицами большой энергии, ударной ионизации, введения носителей заряда в полупроводник из другого тела (инжекция) и др. Возникшие таким образом избыточные носители заряда называются неравновесными. Таким образом, полная концентрация носителей заряда равна:

где n_о и р_о — равновесная концентрация, а Δn и Δр — неравновесная концентрация электронов и дырок. Если возбуждение избыточных электронов производилось из валентной зоны, а полупроводник однородный и не содержит объемного заряда, то концентрация избыточных электронов равна концентрации избыточных дырок:

Рассмотрим характер распределения неравновесных носителей по энергиям. В большинстве случаев при возбуждении электрону сообщается энергии больше, чем ширина запрещенной зоны. Например, это имеет место в случае возбуждения электронов квантами света большой энергии, как показано на рис. 9.1.

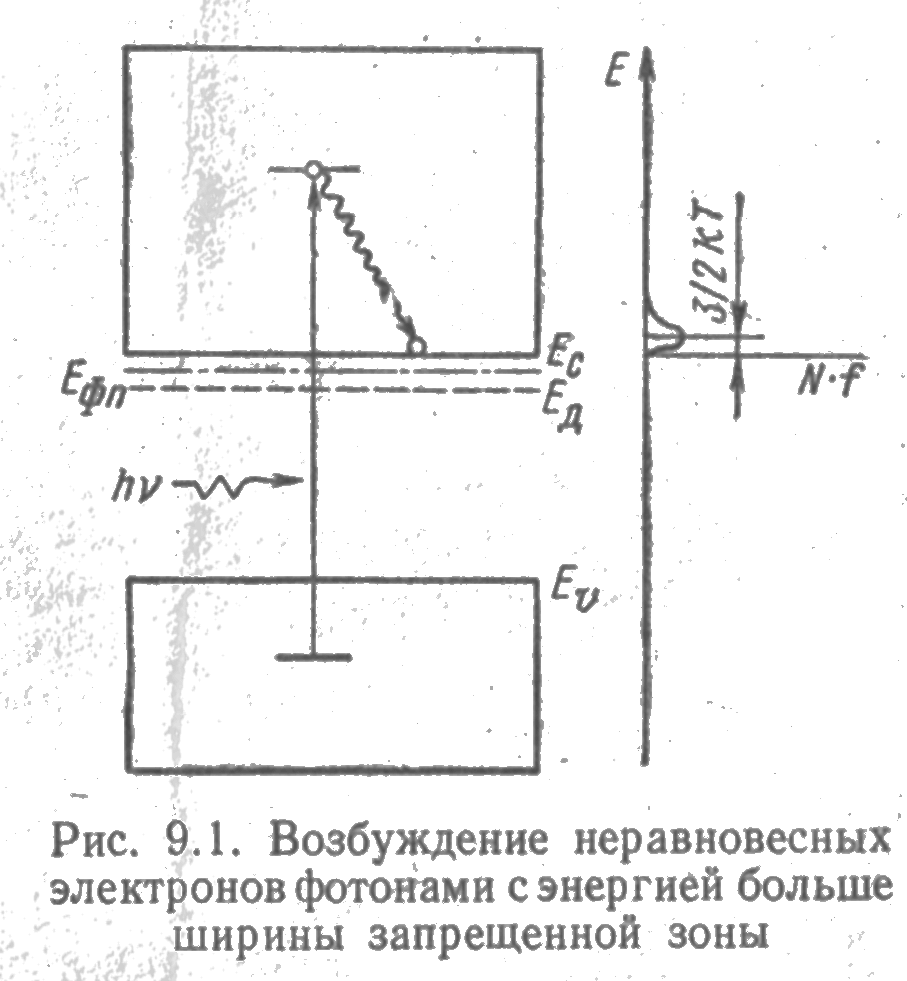
В результате такого возбуждения избыточные электроны оказываются на более высоких энергетических уровнях, чем равновесные электроны, а кинетическая энергия неравновесных носителей оказывается значительно больше средней энергии 3/2 kT.

Однако в дальнейшем в результате рассеяния на фононах и дефектах решетки кинетическая энергия неравновесных носителей быстро снижается до нормальных значений. Расчет показывает, что при длине свободного пробега ≈10^-6 см и скорости электронов 10⁷ см/сек электрон теряет свою избыточную энергию за время порядка 10^-10 сек, претерпев при этом около 10³ актов рассеяния. Таким образом, можно считать, что избыточные носители практически сразу же после возбуждения оказываются распределенными по энергиям, так же как и равновесные носители. Следовательно, возбуждение неравновесных носителей приводит лишь к изменению концентрации свободных носителей, в то время как распределение по энергиям в зонах и средняя кинетическая энергия каждого носителя остаются неизменными.

Как было показано в гл. 7, концентрация равновесных носителей однозначно определяется положением уровня Ферми. Очевидно, неравновесная концентрация носителей уже не может описываться теми же формулами, что и равновесная. Однако в большинстве случаев оказывается удобным полную концентрацию носителей описать с помощью некоторых энергетических уровней, которые входили бы в выражения для полных концентраций таким же образом, как уровень Ферми в формулы (7.21) и (7.25), т. е.

Соответствующие уровни с энергией Е'_Фn и Е'_Фp называются квазиуровнями Ферми. Следует подчеркнуть, что если в равновесии уровень Ферми для электронов и дырок в зонах или в локальных состояниях один и тот же, то квазиуровни Ферми для валентной зоны, зоны проводимости, а также для локальных энергетических состояний различны.

Таким образом, введение понятия о квазиуровне Ферми является формальным приемом, а расстояние от этого квазиуровня до соответствующих энергетических состояний есть просто способ; задания величины концентрации носителей в этих состояниях.

Как уже было отмечено распределение неравновесных носителей по энергиям в зонах по существу не отличается от равновесного. Следовательно, и подвижность неравновесных носителей практически не отличается от подвижности равновесных электронов и дырок. Поэтому выражение для полной электропроводности можно записать как

а выражение для неравновесной электропроводности примет вид

После прекращения действия механизма, вызвавшего появление неравновесной концентрации носителей, происходит постепенное возвращение к равновесному состоянию. Процесс установления равновесия заключается в том, что каждый избыточный электрон при встрече с вакантным местом (дыркой) занимает его, в результате чего пара неравновесных носителей заряда исчезает. Явление исчезновения пары носителей получило название рекомбинации. В свою очередь возбуждение электрона из валентной зоны или примесного уровня, сопровождающееся появлением дырки, называется генерацией носителей заряда.

Следует отметить; что рекомбинация носителей: заряда имеет место также и в равновесных полупроводниках, однако взамен каждой рекомбинируемой пары вследствие термического возбуждения генерируется новая пара носителей заряда. Таким образом, в кристалле в условиях равновесия поддерживается постоянная концентрация; при этом процессы генерации и рекомбинации не принимаются во внимание.

Время жизни

Каждый неравновесный носитель заряда, возбужденный каким-либо образом, проводит в свободном состоянии некоторое время до рекомбинации, которое может быть различным для разных носителей заряда. Поэтому вводят среднее время жизни в возбужденном состоянии электрона τ_n (или дырки τ_р), величина которого может меняться для различных материалов в широких пределах.

Рассмотрим подробнее процесс рекомбинации неравновесных носителей. Пусть с помощью какого либо механизма в полупроводнике возникли избыточные носители с концентрацией Δn_o = Δр_o и к началу отсчета времени (t=0) этот механизм выключился. Начиная с этого момента, концентрация избыточных носителей за счет рекомбинации будет постепенно понижаться, причем скорость рекомбинации, т.е. число рекомбинируемых пар носителей в единицу времени, будет равно Δn/τ_n где Δn — текущая неравновесная концентрация. Тогда можно составить, следующее уравнение:

Решая это уравнение при условии, что Δn (t=0) = Δn_o, получим

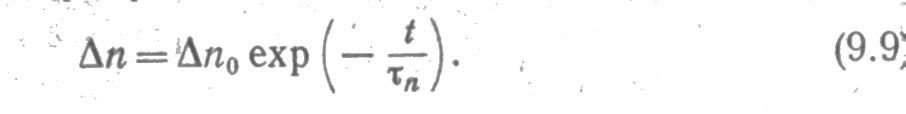
Полученное решение иллюстрируется pиc. 9.2. Из этого решения видно, что процесс рекомбинации описывается экспоненциальной зависимостью от времени, причем среднее время жизни представляет собой такой отрезок, времени, за который концентрация избыточных носителей изменяется в е раз.

Время жизни электрона определяется как среднее время между двумя встречами электрона с дыркой. Действительно, неравновесный электрон, двигаясь в зоне проводимости, имеет определенную вероятность встретиться с дыркой. Поскольку каждая такая встреча с дыркой заканчивается захватом электрона, если дырка неподвижна и расположена на каком-либо локальном уровне, или рекомбинацией, если дырка находится в валентной зоне, то средний отрезок времени между моментом генерации неравновесного электрона и моментом столкновения, его с дыркой является временем жизни.

Способность дырки к захвату электрона характеризуется параметром «сечение захвата». Для определения этого параметра проведем через дырку плоскость, перпендикулярную направлению движения электрона. При пересечении этой .плоскости электрон будет захвачен дыркой, если расстояние между ними окажется небольшим, или пройдет мимо, если это расстояние будет значительным. Площадь той части плоскости, при пересечении которой электрон еще захватывается дыркой, называется эффективным сечением захвата (рекомбинации) или просто сечением захвата. Сечение захвата зависит от ряда факторов, в том числе от относительной скорости взаимодействующий частиц, природы ионизированного атома, условий экранирование дырки другими свободными носителями и др.

Пользуясь понятием о сечении захвата, можно определить время жизни. Действительно, число возможных встреч данного электрона с дырками в единицу времени, очевидно, равно произведению концентрации дырок р, средней относительной скорости движения электрона и дырки υ_np и сечению захвата электрона дыркой s_n. Среднее время жизни, равное времени пробега электрона между такими встречами с дыркой, очевидно, выразится как

В процессе захвата и рекомбинации электронов могут участвовать дырки различной природы, а именно: свободные дырки в валентной зоне, дырки, локализованные на различных примесных уровнях, дефектов: решетки и т. п. Каждый тип дырок, естественно, может иметь свое значение концентрации, сечения захвата и относительной скорости. Поэтому по отношению к к-му типу дырок может быть введено свое значение времени жизни электрона:

В этом случае процесс рекомбинации электронов идет параллельно по различным механизмам и, следовательно, интенсивнее, а эффективное время жизни электронов в зоне проводимости складывается из составляющих времен жизни по отношению к каждому типу дырок:

Изложенные соображения относились к вычислению времени жизни электронов в зоне проводимости, однако они в полной мере применимы и при вычислении времени жизни дырок в валентной зоне. Так, аналогично (9.11) можно записать:

где n_к—концентрация электронов некоторого типа (свободных или находящихся на примесных уровнях, уровнях дефектов и др.), способных захватить дырку; υ_npк - скорость дырки относительно соответствующего типа электрона, a s_pk—сечение захвата этим электроном дырки. Эффективное время жизни дырок в зоне проводимости определяется по формуле, аналогичной (9.12).

Произведение сечения захвата s_nк и относительной скорости υ_npк усредненное по всем носителям в зоне,

принято называть коэффициентом рекомбинации (или, захвата). C учетом этого обозначения формулы (9.11) и (9.13) примут вид:

В легированных полупроводниках обычно время жизни неравновесных носителей относят к неосновным носителям: в случае электронного полупроводника говорят о времени жизни дырок и, наоборот, в случае дырочного полупроводника — о времени жизни электронов. Это обстоятельство вызвано тем, что в большинстве случаев концентрация избыточных основных носителей обычно меньше концентрации равновесных основных носителей, в то время как избыточная, концентрация неосновных носителей может превышать их равновесную концентрацию. Поэтому, процесс рекомбинации будет протекать медленнее для неосновных носителей, имеющих меньшую концентрацию, чем для основных, как эта видно из формул (9.15),и (9.16) при условии, что коэффициенты рекомбинации γ_nk и γ_pk одного порядка. Таким образом, процесс рекомбинации неравновесных носителей ограничивается временем жизни неосновных носителей.

Следует отметить, что, поскольку время жизни неравновесных носителей зависит от концентрации р_к и n_к, то оно не является константой материала, а меняется с изменением температуры, концентрации примесей и дефектов решетки, а также во времени при нестационарных условиях, когда в процессе генерации, рекомбинации или переноса концентрация носителей заряда существенно изменяется. В реальных условиях среднее время жизни носителей в полупроводниках составляет 10^-2 — 10^-8 сек.

При каждом акте рекомбинации электрона и дырки выделяется энергия, равная энергетическому промежутку между уровнями этих частиц. Эта энергия может выделяться либо в виде кванта света (излучательная рекомбинация), либо в виде тепловой энергии (фонона), передаваемой атомам решетки (безызлучательная рекомбинация). Как показывают расчеты и экспериментальные исследования, излучательная рекомбинация играет относительно малую роль в реальных полупроводниках, за исключением полупроводников с малой шириной запрещенной зоны и с прямыми междузонными переходами. Например, расчет показывает, что для собственного германия при комнатной температуре время жизни по отношению к излучательной рекомбинации электрон—дырка составляет примерно 1 сек, в то время как время жизни электронов по отношению к безызлучательной рекомбинации составляет около 10^-3 сек. В свою очередь в антимониде индия, имеющем узкую ширину запрещенной зоны ΔЕ = 0,18 эв, определяющим является механизм излучательной рекомбинации, поскольку время жизни электрона по отношению к этому механизму составляет 10^-7 сек.

Процесс безызлучательной рекомбинации в подавляющем большинстве случаев проходит с выделением фонона. Однако прямая междузонная безызлучательная рекомбинация электрон-дырка также маловероятна, поскольку выделяющаяся энергия порядка ширины запрещенной зоны 1—2 эв не может быть поглощена одним фононом, а одновременное участие многих фононов маловероятно. Поэтому наиболее распространенным видом является безызлучательная рекомбинация через промежуточные уровни примесей и дефектов. При этом процесс рекомбинации осуществляется в два этапа. Вначале электрон захватывается локальным центром (ловушкой), представляющим собой примесный атом или дефект решетки, а затем этим же центром захватывается дырка, или, иными словами, электрон с этого центра переходит в валентную зону. Очевидно, что при таком двухэтапном процессе рекомбинации электрон отдает решетке свою энергию по частям в виде двух фононов. Возможна также рекомбинация через несколько локальных центров рекомбинации. В этом случае энергия, выделяемая при рекомбинации электроном, передается решетке в виде нескольких фононов. Наиболее интенсивно осуществляется рекомбинация через такие центры, энергетические уровни которых -расположены в средней части запрещенной зоны.

Следует отметить, что механизм безызлучательной рекомбинации через локальные уровни оказывается наиболее, вероятным даже при крайне малой концентрации рекомбинационных центров порядка 10¹² см^-3 и ниже. Лишь при очень высокой концентрации избыточных носителей существенную роль будет играть прямая рекомбинация.

Следует, однако, иметь в виду, что эффективность рекомбинации через примесные центры определяется не только вероятностью захвата электрона и дырки этими центрами, но и вероятностью обратных тепловых забросов носителей в зоны. Действительно, захват ловушкой например, электрона из зоны проводимости лишь в том случае завершится рекомбинацией пары, если электрон будет находиться на локальном уровне до тех пор, пока на этот же уровень не перейдет из валентной зоны дырка. Обратный тепловой заброс электрона в зону проводимости, очевидно, ликвидирует такую возможность и, следовательно, приведет к уменьшению интенсивности рекомбинации. Такие ловушки, для которых вероятность обратного теплового заброса очень велика, практически находятся в обмене зарядами только с одной из зон и не способствуют; процессу рекомбинации. Эти ловушки называются центрами (уровнями) прилипания.

В противоположность этому ловушки, для которых тепловые забросы маловероятны, именуются центрами рекомбинации.

Разумеется, такое деление ловушек на центры прилипания и центры рекомбинации довольно грубое, поскольку та или другая роль ловушек зависит от температуры, концентрации носителей заряда и т. д.

Рекомбинация на примесных центрах. Рекомбинация в объеме

Как уже было отмечено, мелкие примесные уровни в полупроводниках практически не влияют на процессы рекомбинации электрона с дыркой. Эти уровни легко обмениваются электронами с прилегающей зоной, однако вероятность перехода электрона из зоны проводимости на акцепторный уровень или дырки из валентной зоны на донорный уровень крайне мала и практически не отличается от вероятности прямой рекомбинации электрон — дырка. Поэтому процессу рекомбинации могут способствовать лишь уровни, находящиеся вблизи середины запрещенной зоны. В моноатомных полупроводниках такие глубокие уровни могут быть созданы введением в них золота, меди, железа, кобальта, никеля, платины и др. В большинстве случаев эти примеси являются многозарядными, т. е. обладают способностью отдавать или захватывать несколько электронов или дырок. Так, атом меди, замещая в решетке атом германия, захватывает три электрона, оставляя в валентной зоне три дырки. Энергия ионизации атома меди не для всех электронов одинакова, а составляет 0,04; 0,32 и 0,46 эв. Соответственно каждый атом меди образует в германии три энергетических уровня, как показано на рис. 9.3.

Наличие нескольких уровней может существенно способствовать процессу рекомбинации, однако обычно главную роль играет уровень, расположенный в средней части запрещенной зоны. Учитывая сказанное, а также в связи с тем, что рассмотрение процесса рекомбинации на нескольких уровнях представляет сложную задачу, ограничимся случаем, когда рекомбинация проходит лишь с участием одного уровня Е_t, находящегося на Δ Е_t ниже дна зоны проводимости, как показано на рис. 9.4. Для этого случая найдем выражение для времени жизни неравновесных носителей.

На рис. 9.5 показаны наиболее важные переходы при рекомбинации с участием одного уровня. Вероятность захвата электрона ловушкой, расположенной на уровне Е_t, пропорциональна числу электронов в зоне проводимости n и числу пустых атомов примеси, равному N_t(1—f), где N_t — общая концентрация центров рекомбинации, а f – степень их заполнения электронами. Вероятность обратного процесса возбуждения электрона с этого уровня в зону проводимости пропорциональна числу электронов на них, равному N_tf.

В итоге изменение числа электронов в зоне проводимости вследствие захвата в единицу времени будет равно

(9.17)

где γ_n — коэффициент захвата электрона локальным центром, а β_n — некоторая постоянная, не зависящая от n и f. Соотношение между этими постоянными может быть определено из условия теплового равновесия. В состоянии теплового равновесия dn/dt = 0, концентрация электронов описывается формулой (7.21), а значение функции распределение на примесном уровне Е_t задается формулой

Подставляя зги .величины в (9.17), получим

Видно, что n₁ представляет собой концентрацию равновесных электронов в таком образце, в котором уровень Ферми совпадает с уровнем центров рекомбинации. С учетом (9.19) уравнение (9.17) перепишется так:

Аналогично вероятность захвата дырок ловушкой, или, что то же самое, вероятность перехода электрона с примесного центра в валентную зону пропорциональна числу дырок в валентной зоне р и концентраций атомов примеси, заполненных электронами, которое равно N_tf. Число же обратных переходов пропорционально числу дырок на примесном уровне, равному N_t(1—f). Таким образом, аналогично (9.20) для дырок имеем

где γ_р — коэффициент захвата дырки локальным центром, а р₁ — концентрация дырок в валентной зоне при условии, что уровень Ферми совпадает с примесным уровнем.

Запишем далее уравнение для баланса числа электронов на примесном уровне. Изменение числа электронов на рекомбинационных центрах, которое выражается членом N_tdf/dt, равно разности числа электронов, приходящих из зоны проводимости dn/dt, и числа электронов, уходящих в валентную зону в единицу, времени dp/dt, т. е.

В соответствии с условием нейтральности начальные значения концентрации избыточных носителей Δn и Δp должны быть связаны следующим уравнением

где Δf==f-f_о, а слагаемое N_tΔf равно концентрации избыточных электронов на примерном уровне. Поскольку в большинстве случаев концентрация центров рекомбинаций крайне мала и обычно не превышает концентрацию избыточных носителей т. е. N_tΔf<<Δn, то уравнение (9.23) принимает вид

Это значит, что степень заполнения примесных уровней практически не изменяется в процессе рекомбинации. Тогда (9.22) перепишется так:

Приравнивая (9.20) и (9.21), найдем неравновесную функцию распределения:

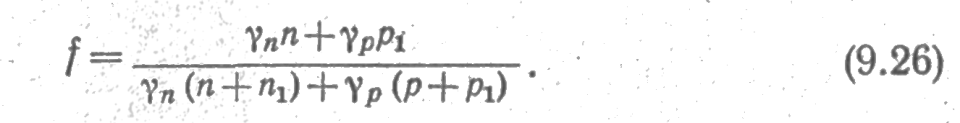
Подставляя значение этой функции в (9.20) и учитывая, что n₁p₁= n_i²=n₀p₀,получим

При условии, что избыточная концентрация меньше концентраций основных носителей, имеем

Учитывая, что изменение концентрации неосновных носителей описывается уравнением (9.8), из (9.27) получим общее выражение для времени жизни неравновесных носителей

Рассмотрим это выражение применительно к нескольким частным случаям. В случае сильно легированного полупроводника n-типа можно принять следующие соотношения

С учетом этих соотношений выражение (9.29) принимает

Следовательно, в этом случае получаем время жизни неосновных носителей — дырок, зависящее только от концентрации центров рекомбинации и коэффициента захвата дырок этими центрами. Обычно коэффициент захвата слабо зависит от температуры, поэтому τ_ро также практически постоянно.

Аналогичная ситуация наблюдается в случае сильно легированного полупроводника р-типа:

В этом случае получаем время жизни неосновных носителей - электронов

которое зависит только от концентрации центров рекомбинации и коэффициента захвата электронов этими центрами и также слабо изменяется с температурой.

Для того чтобы выполнялись условия (9.30), необходимо, чтобы уровень Ферми проходил выше уровня Е_t, если последний лежит выше середины запрещенной зоны (см. рис. 9.4, а), или выше уровня Е_t^' = E_υ + ΔЕ_t, если уровень E_t лежит ниже середины запрещенной зоны (см. рис. 9.4, б). Соответствующим образом должен располагаться уровень Ферми для того, чтобы выполнялись условия (9.32).

Выражение (9.29) можно переписать иначе, используя (9.31) и (9.33), а именно:

При повышении температуры или при уменьшении степени легирования полупроводника, когда уровень Ферми приближается к середине запрещенной зоны ближе, чем Е_t, концентрации n и р будут значительно меньше, чем n₁ и р₁ соответственно. Тогда формула (9.34) примет вид

В этом случае время жизни зависит от концентрации равновесных носителей, а следовательно, и от температуры. Учитывая закон действующих масс, нетрудно видеть, что время жизни достигает максимума при n₀ = р_о = n_i т. е. когда

Поскольку n₁ либо p₁ всегда больше n_i, то при τ_no ≈ τ_po время жизни в собственном полупроводнике τ_i всегда больше времени жизни в легированном полупроводнике τ_no или τ_po.

На основании изложенного можно сделать следующие выводы. В сильно легированных полупроводниках, пока уровень Ферми находится вблизи дна зоны проводимости или вблизи потолка, валентной зоны, время жизни неравновесных неосновных носителей минимально, практически не зависит от температуры и определяется формулами (9.31) и (9.33) для неосновных носителей заряда — дырок и электронов соответственно. При перемещении уровня Ферми в среднюю часть запрещенной зоны, что может быть достигнуто либо увеличением температуры в легированных полупроводниках и переходом в область собственной проводимости, либо снижением степени легирования и переходом к собственным полупроводникам, время жизни увеличивается в соответствии с (9.35) и достигает максимального значения при n₀ = р_о = n_i, равного (9.36). На рис. 9.6 показана зависимость времени жизни заряда от положения уровня Ферми, иллюстрирует сделанные выводы.

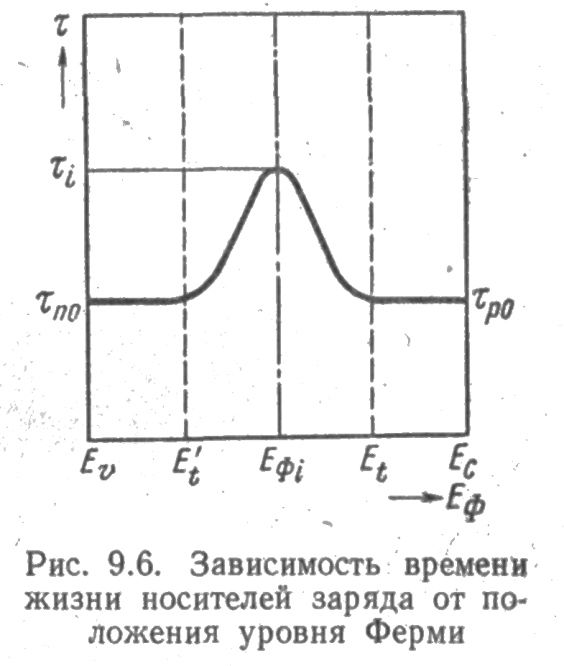
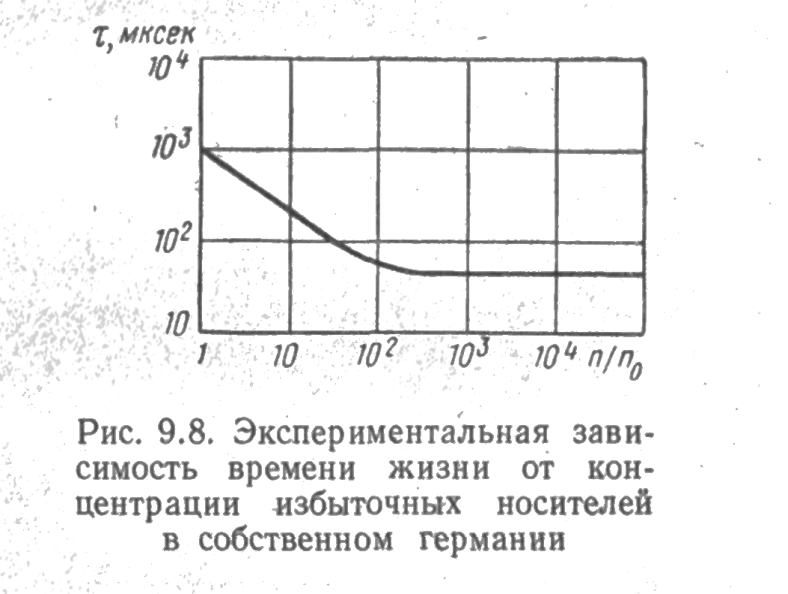
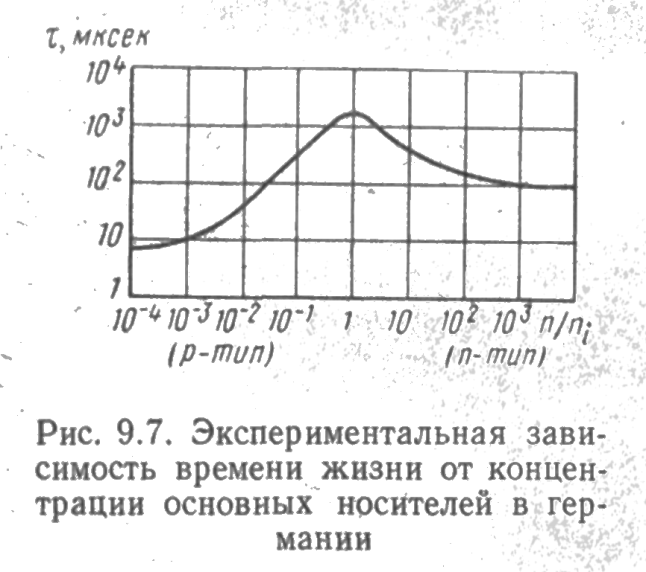
Вычисленные, зависимости хорошо согласуются с результатами экспериментальных исследований. Так, на рис. 9.7 приведена экспериментальная зависимость времени жизни носителей заряда в германии от концентрации основных носителей n₀/n_i или p_o/p_i при постоянной концентрации центров рекомбинации. Нетрудно видеть, что максимум кривой приходится на значение n₀ = n_i, а времена жизни τ_no и τ_po отличаются друг от друга более чем на порядок.

При выводе формулы для времени жизни предполагалось, что концентрация избыточных носителей значительно меньше концентраций основных носителей в полупроводнике. Однако в некоторых практических случаях соотношение может быть обратным. С увеличением концентрации избыточных носителей время жизни должно, очевидно, уменьшаться. Выражение, для времени жизни с учетом концентрации избыточных носителей, аналогичное (9.34), имеет вид

Из (9.37) видно, что в случае, когда избыточная концентрация значительно превышает равновесную концентрацию, т.е. когда Δn>>n₀, p₀, n₁, p₁, время жизни перестает зависеть от концентрации и равняется

На рис. 9.8 показана экспериментальная зависимость времени жизни от концентрации избыточных носителей в собственном герма-