171

Раздел II. Микроэлектроника

Введение

(Физические основы микроэлектроники)

Глава 1. Основы физики кристаллов

§ II.1.1. Идеальные кристаллы

§ II.1.2. Виды химической связи между атомами в кристаллах

§ II.1.3. Равновесное, состояние решетки

§ II.1.4. Реальные кристаллы

Глава 2. Диффузионные процессы в твердых телах

§ II.2.1. Механизм диффузии

§ II.2.2. Математическая теория диффузионных процессов

§ II.2.3. Диффузия примесей в германии и кремнии

§ II.2.4. Окисление кремния

Глава 3. Зонная теория твёрдого тела

§ II.3.1. Уравнение Шредингера, для кристалла

§ II.3.2. Энергетические зоны

§ II.3.3. Зоны Бриллюэна

§ II.3.4. Степень заполнения энергетических зон

§ II.3.5. Энергетические уровни дефектов и примесей в полупроводниках

Глава 4. Статистика носителей заряда в твердом теле

§ II.4.1. Функции распределения частиц по энергиям.

§ II.4.2. Сравнение функций распределения

§ II.4.3. Концентрация носителей заряда в собственном и

слабо легированном полупроводниках

§ II.4.4. Концентрация носителей заряда в сильно легированном

полупроводнике и металле

Глава 5. Явления переноса носителей заряда в твердом теле

§ II.5.1. Электропроводность полупроводников и металлов

§ II.5.2. Механизмы рассеяния и подвижность

свободных носителей заряда

§ II.5.3. Особенности контактных явлений

Глава 6. Оптические и фотоэлектрические явления в полупроводниках

Глава 7. Схемотехника и технология производства ИМС

§ II.7.1. Представление об элементной базе

и радиоэлектронной аппаратуре различных поколений

§ II.7.2. Основные принципы проектирования устройств

дискретной и интегральной электроники

§ II.7.3. Основные критерии миниатюризации

и оптимизации изделий микроэлектроники

§ II.7.4. Ограничения и проблемы электроники твердого тела

§ II.7.5. ТТЛ технология производства ИМС

§ II.7.6. МДП технология производства ИМС

§ II.7.7. БИС - проблемы и ограничения

§ II.7.8. Конструкция ИМС. Материалы и виды обработки,

применяемые при изготовлении ИМС

РАЗДЕЛ II

Микроэлектроника

Введение

§ II.1.1. Основы физики кристаллов

Кристаллом называется твердое тело, состоящее из атомов (ионов или молекул), расположенных с периодической повторяемостью в трех измерениях.

Идеальный кристалл можно построить путем бесконечного закономерного повторения в пространстве одинаковых структурных единиц. В наиболее простых кристаллах структурная единица состоит из одного атома. В более сложных кристаллах структурная единица может содержать несколько атомов или молекул.

Понятие о кристаллической решетке.

Любую кристаллическую структуру можно описать с помощью периодически повторяющейся в пространстве элементарной части кристаллической решетки, называемой элементарной ячейкой (имеющей форму параллелепипеда), с каждой точкой которой связана некоторая группа атомов. Эта группа атомов называется базисом; базис повторяется в пространстве и образует кристаллическую решетку.

Трансляционная решетка Бравэ.

Огюст Бравэ 1848 г. Впервые ввел понятие кристаллической решетки. Возьмем три независимых базисных вектора a₁, а₂, а₃ исходящих из одной точки и построим результирующий вектор

.

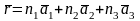Если n₁, n₂, n₃ принимают последовательно все целочисленные значения, то формируется пространственная решетка, обладающая периодичностью по всем трем направлениям. В кристаллографии за единицу измерения обычно принимают размер векторов a₁, а₂, а₃ и в этом случае эти вектора называются осевыми единицами.

Параллелепипед, образованный базисными векторами называют элементарной ячейкой. 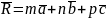Длину ребра элементарной ячейки вдоль одной из осей называют постоянной решетки. Поскольку α, β, γ – углы между базисными векторами могут принимать различные значения, то элементарная ячейка может иметь форму косоугольного параллелепипеда, призмы или куба. Постоянные решетки в разных направлениях также могут быть различными. Решетки данного вида принято называть простыми. Ячейки, в которых атомы располагаются не только в вершинах, называются сложными.

Более сложные пространственные решетки могут быть получены из простых решеток, взаимно сдвинутых на определенную величину. Простую решетку имеют обычно одноатомные кристаллы. Двух-, трёх-, четырехатомные кристаллы имеют более сложную решетку, состоящую соответственно из двух, трех или четырех вдвинутых друг в друга простых решеток.

Во всех вершинах элементарной ячейки располагаются одинаковые атомы или группы атомов поэтому все вершины ячеек эквивалентны друг другу и их называют узлами решетки. Элементарные ячейки, атомы в которых располагаются только в вершинах называется простыми или примитивными, на каждую такую ячейку в среднем приходится один узел.

Важнейшим параметром кристаллической решетки является координационное число, указывающее число ближайших частиц, окружающих данную частицу кристалла. Например, для кристалла NaCl координационное число равно 6. Каждый атом Na окружен шестью ионами Cl, а каждый ион Cl – шестью ионами натрия.

Существуют пять типов двухмерных решеток, а трехмерных пространственных решеток будет уже четырнадцать. Пространственные решетки Браве показаны на рис. 1.14.

По взаимному расположению и соотношению базисных векторов кристаллические решетки объединяются в системы (сингонии: син. лат. – одинаковый, гон. лат. – угол), то есть видов кристаллических решеток, обладающих сходными элементарными ячейками.

Сингоний семь: триклинная, моноклинная, ромбическая, тетрогональная, ромбоэдрическая, гексогональная, кубическая.

Каждая кристаллическая система состоит из нескольких видов кристаллических решеток. Всего существуют четыре вида кристаллических решеток: простая, базоцентрированная, объемоцентрированная и гранецентрированная. Каждая из этих кристаллических решеток может быть представлена совокупностью двух или большего числа простых подрешеток, смещенных относительно друг друга. В общей сложности имеется 14 видов различных решеток, называемых решетками Бравэ. Среди них, например: ОЦК – объёмоцентрированные (железо, вольфрам); ГЦК – гранецентрированные (медь, алюминий, свинец, никель и т.д.).

Для обозначения положения какой либо плоскости, проходящей через какие-либо три узла кристаллической решетки, или совокупности параллельных плоскостей используются индексы Миллера. Существуют три категории индексов Миллера: индекс узлов, индекс направлений, индекс плоскостей.

Рис. 1.14. Четырнадцать пространственных решеток Браве. Показаны обычно используемые ячейки, которые не всегда являются примитивными. Р — символ примитивной ячейки, I — объемноцентрированной, F — гранецентрированной, С — с центрированными основаниями, R — ромбоэдрической.

Индексы плоскости.

Если за начало координат взять один из узлов пространственной решетки, а за оси x, y, z – любые три ряда узлов, то любая кристаллическая плоскость будет отсекать от осей отрезки х = mа₁, y = nа₂, p =a₃ , где m, n, p – простые числовые параметры грани. Для определения индексов Миллера необходимо взять обратные значения этих простых числовых параметров грани (1/m; 1/n; 1/p) и привести их к общему знаменателю (h/s; k/s; l/s) и отбросить его. Числа (h, k, l) и являются индексами Миллера. Если плоскость параллельна координатной оси, то соответствующий индекс Миллера будет равен нулю. Все плоскости, имеющие одинаковые индексы Миллера являются параллельными.

Для примера на рисунке изображены три главные плоскости простой кубической решетки.

Рис. 1.21. Индексы Миллера некоторых наиболее важных плоскостей кубического кристалла. Плоскость (200) параллельна плоскости (100)

Набор индексов (hkl) может означать отдельную плоскость или семейство параллельных плоскостей. Если плоскость пересекает ось в области отрицательных значений координат, соответствующий индекс также будет отрицательным, но знак минус в этом случае помещается не перед индексом, а над ним, — например, . Плоскости граней кубического кристалла имеют индексы (100), (010), (001), , 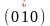и . Плоскости, эквивалентные по характеру симметрии, обозначаются индексами, помещаемыми в фигурные скобки; например, все грани куба можно обозначить через {100}. Часто просто говорят— плоскости (100). Плоскость (200)—это плоскость, параллельная плоскости (100), но отсекающая на оси а отрезок вдвое меньший, чем плоскость (100). На рис. 1.21а—1.21в показано образование плоскостей (110), (111) и (322) в кубической гранецентрированной структуре, если за исходные атомные плоскости взяты плоскости (100).

Индексы направлений.

Для обозначения направлений в кристалле применяются индексы, представляющие собой набор наименьших целых чисел, относящихся между собой как компоненты вектора, параллельного данному направлению в соответствующей системе координат. Эти целые числа в случае направлений пишутся в квадратных скобках: [hkl].

Рис. 1.22. Координаты центральной точки ячейки, выраженные в долях длин векторов

а, b, с, равны

В кубических кристаллах направление оси x запишется как [100], отрицательное направление оси y как 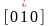. Часто через [hkl] обозначают и эквивалентные направления, которые просто называют [hkl]-направлениями. В кубических кристаллах направление [hkl] всегда перпендикулярно к: плоскости (hkl), имеющей те же индексы (см. задачу 1.3), однако для кристаллов других систем это, вообще говоря, не имеет места.

Индексы узлов элементарной ячейки

Положение узла элементарной ячейки задается координатами, которые выражаются в долях длин векторов а, b, с; начало координат выбирается в вершине угла элементарной ячейки. Таким образом, например, в кубической решетке центральный узел имеет координаты (рис. 1.22), а узлы в центрах граней — координаты 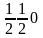; ; 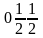. Координаты атомов в ГЦК и ОЦК решетках находятся обычно по координатам узлов соответствующей элементарной кубической ячейки. В таблицах с характеристиками кристаллических структур обычно указывается тип и размер элементарной ячейки, а затем приводятся значения координат каждого атома ячейки.

Признаки симметрии кристаллов:

Периодичность структуры - дальний и ближний порядок.

Анизотропия (зависимость свойств от направлений).

Симметрия (соразмерность) обозначает вид согласованности отдельных частей, которые объединяет их в единое целое. Элементы симметрии:

Центр симметрии.

Оси симметрии.

Плоскости симметрии.

Порядок симметрии. Порядком оси симметрии – называется число, показывающее сколько раз совмещается сам с собой кристалл при повороте его вокруг данной оси на 360 .

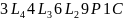– формула симметрии куба.

где L – ось симметрии;

P – плоскость симметрии;

C – центр симметрии.

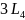- три оси четвертого порядка.

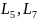и более высоких порядков осей не существует.

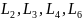- у минералов.

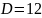
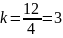
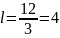
Плоскости эквивалентные по характеру симметрии обозначаются индексами помещенные в фигурные скобки. Например, все грани куба можно обозначить .

Совокупность направлений перпендикулярных граням 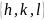обозначают

Пример: заменяет совокупность

Простые кристаллические структуры

Ниже мы кратко опишем некоторые простые кристаллические структуры, представляющие общий интерес; к ним относятся, в частности, структуры хлористого натрия, хлористого цезия, гексагональная структура с плотной упаковкой, структура алмаза и кубическая структура сульфида цинка.

Структура хлористого натрия. Структура хлористого натрия, NaCl, показана на рис. 1.23. Решетка Браве — кубическая гранецентрированная. Базис состоит из двух атомов: одного атома Na и одного атома Cl, находящихся один от другого на расстоянии, равном половине длины пространственной диагонали элементарного куба. Элементарный куб содержит четыре молекулы натрий хлор. Атомы имеют следующие координаты:

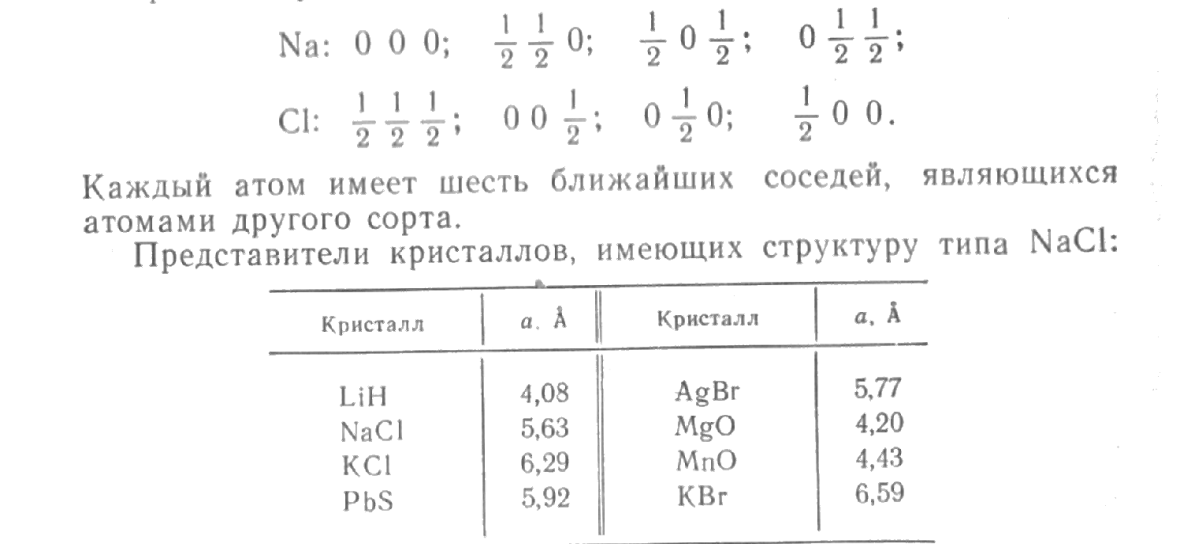
Рис. 1.23. Кристаллическая структура хлористого натрия. Пространственной решеткой является гранецентрированная кубическая решетка, а базис состоит из ионов 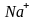с координатами 000 и иона с координатами

Поскольку любое направление в кристалле определяется прямой, проходящей через начало координат и первый узел на этом направлении. Эти индексы обычно записываются в квадратных скобках [unw] – индекс направления. В кубической системе индексы плоскости и индексы направления, перпендикулярного данной плоскости совпадают.

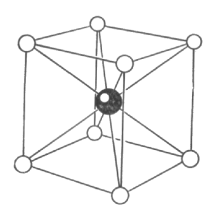
Рис. 1.24. Кристаллическая структура хлористого цезия. Пространственной решеткой является простая кубическая решетка, а базис состоит из ионов 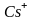с координатами 000 и иона с координатами

Значения а приведены в ангстремах; 1 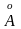= 10^-8 см = 10^-10 м.

Структура хлористого цезия. Структура хлористого цезия СsСl показана на рис. 1.24. В структуре хлористого цезия на элементарную ячейку приходится одна молекула. Базис содержит один атом Сs с координатами 000 и один атом хлора с координатами .

Пространственная решетка - простая кубическая. Каждый атом, являющийся центром, куба, имеет соседями в углах этого куба атомы другого сорта, так, что координационное число равно восьми.

Представители кристаллов, имеющих структуру типа СsС1:

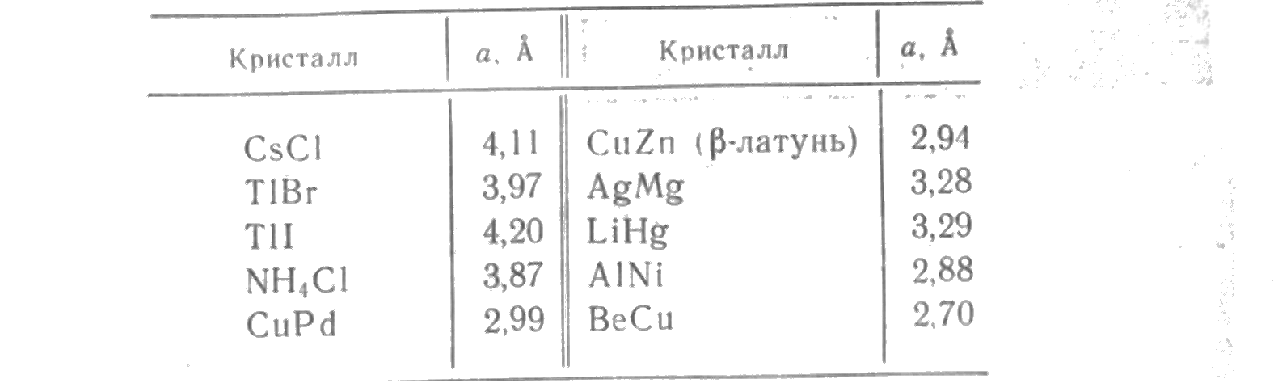
(Кристаллические структуры, имеющие простую кубическую решетку Браве, вообще говоря, не редкость, однако химические элементы «предпочитают» не кристаллизоваться в такие структуры, для которых характерны отсутствие плотнейшей упаковки и направленность связей.)

Гексагональная структура с плотной упаковкой. Расположить одинаковые твердые шары в пространстве так, чтобы объем, остающийся между ними, был минимален, можно двумя способами (рис. 1.27а). Один способ приводит к структуре, обладающей кубической симметрией, а именно к гранецентрированной кубической структуре (кубическая структура с плотной упаковкой), другой — к структуре, обладающей гексагональной симметрией и носящей название гексагональной структуры с плотной упаковкой (рис. 1.27в). Часть общего объема, занятая твердыми шарами, составляет 0,74 как для кубической, так и для гексагональной структур с плотной упаковкой.

Шары можно уложить плотноупакованным плоским слоем так, чтобы каждый шар соприкасался с шестью другими. Этот слой может быть либо базисной плоскостью гексагональной структуры с плотной упаковкой, либо плоскостью (111) гранецентрированной кубической структуры. Второй такой слой можно уложить на первый таким образом, чтобы каждый его шар прикасался с тремя шарами нижнего слоя, как показано на рис. 1.27а. Следующий, третий слой может быть уложен двумя способами. В случае кубической гранецентрированной структуры шары третьего слоя расположатся над теми углублениями (лунками) первого слоя, которые не заняты шарами второго слоя; случае гексагональной структуры шары третьего слоя расположатся непосредственно над шарами первого. Чередование слоев для кубической плотной упаковки можно поэтому записать так: АВСАВС...., а для гексагональной — АВАВАВ ....

Рис. 1.27а. Плотноупакованные слои твердых шаров. Центры шаров помечены точками А.

Шары второго слоя можно разместить над шарами первого слоя таким образом, что их центры займут положения В (или, что эквивалентно, положения С). Если шары второго слоя занимают положения В, то укладку шаров третьего слоя можно осуществить двумя способами: помещая их либо над А, либо над С. В первом случае получим последовательность слоев АВАВАВ... и структура является гексагональной структурой с плотной упаковкой. Во втором случае получим последовательность слоев АВСАВСАВС... и структура является кубической структурой с плотной упаковкой. Плоскостью плотной упаковки является плоскость (111).

Рис. 1.276. Гранецентрированная кубическая структура. Один угол срезан для того, чтобы показать плоскость (111). Плоскости (111) являются плотноупакованными слоями твердых шаров.

Элементарная ячейка гексагональной структуры с плотной упаковкой представляет собой примитивную гексагональную ячейку; в базисе её — два атома (см. рис. 1.27г). Примитивная ячейка, выбранная внутри гранецентрированной кубической ячейки, содержит один атом.

Отношение с/а для гексагональной плотноупакованной структуры равно (8/3)^1/2 = 1,633. Условились относить кристаллы к классу имеющих плотноупакованную гексагональную структуру даже в том случае, когда отношение с/а несколько отличается от теоретического значения. Так, цинк, у которого отношение с/а = 1,86 (а = 2,66 Аº, с = 4,94 Аº), должен быть отнесен к числу структур с гексагональной плотной упаковкой, хотя углы между атомными связями в его структуре значительно отличаются от тех, которые присущи идеальной гексагональной структуре с плотной упаковкой. Магний, у которого отношение с/а = 1,623, имеет почти идеальную структуру с гексагональной плотной упаковкой.

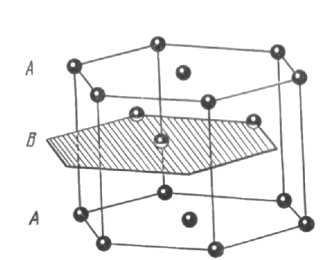
Рис. 1.27в. Гексагональная структура с плотной упаковкой. Расположение атомов в этой структуре не отвечает пространственной решетке. Пространственной решеткой является простая гексагональная решетка, базис которой состоит из двух одинаковых атомов, связанных с каждой точкой решетки.

Рис. 1.27г. Для примитивной ячейки a=b и угол между а и b равен 120°. Ось с перпендикулярна к плоскости, в которой лежат а и b. Для идеальной гексагональной структуры с плотной упаковкой с=1,633а. Два атома, образующие базис, показаны на рисунке черными кружками. Один атом, расположенный в начале координат, имеет координаты 000, второй и связан с началом координат радиус-вектором

Многие металлы при определенных температурах довольно легко изменяют свою структуру с гранецентрированной кубической на структуру с гексагональной плотной упаковкой и наоборот. Заметим, что координационное число, определяемое как число атомов, являющихся ближайшими соседями данного атома, одинаково для обоих видов структур с плотной упаковкой. Ели бы энергия связи зависела только от числа связей атома с соседями, то энергии гранецентрированной кубической структуры и структуры с гексагональной плотной упаковкой были бы одинаковы.

Примеры кристаллов, имеющих гексагональную плотноупакованную структуру:

Структура алмаза. Пространственная решетка алмаза является кубической гранецентрированной. С каждым узлом решетки связан примитивный базис, состоящий из двух одинаковых атомов с координатами 000 и (рис. 1-28).

Рис 1.28 Расположение атомов в элементарной кубической ячейке алмаза (проекция на грань куба). Значения дробей указывают высоту атомов над базисной плоскостью (за единицу длины принято ребро куба). Точки с высотой 0 и 1/2 составляют гранецентрированную кубическую решетку; точки с высотой 1/4 и 3/4, образуют такую же решетку, смещенную вдоль пространственной диагонали куба на четверть ее длины. Базис состоит из двух одинаковых атомов, имеющих координаты 000 и

Тетраэдрическое расположение связей в структуре алмаза иллюстрируется схемой, приведенной на рис. 1.29.

Рис. 1.29 Изображение кристаллической структуры алмаза,

показывающее тетраэдрическое расположение связей

Каждый атом имеет четырех ближайших соседей и двенадцать соседей, следующих за ближайшими. Элементарный куб содержит восемь атомов. Решетка алмаза не относится к числу плотных: максимальный относительный объем, который может быть занят твердыми шарами, имитирующими атомы, составляет лишь 0,34, т. е. примерно 46% от величины коэффициента заполнения, характерной для плотноупакованной структуры.

В структуре алмаза кристаллизуются углерод, кремний, германий и серое олово, постоянные решетки этих кристаллов равны соответственно 3,56; 5,43; 5,65 и 6,46 Аº. В структуре алмаза атомы связаны между собой ковалентными связями.

(Элементарная ячейка алмаза, имеющая форму куба, содержит восемь атомов; если мы будем описывать структуру алмаза посредством такой элементарной ячейки, то получим базис, содержащий восемь атомов. Однако в структуре алмаза не удается выбрать примитивную ячейку таким образом, чтобы базис состоял только из одного атома.)

Таким образом, в основе структуры кристаллов многих металлов и большинства полупроводниковых материалов лежат кубические решетки и их сочетания. В простой кубической решетке атомы расположены в углах элементарной ячейки. Координационное число равно шести (NaCl, KCl). В объемноцентрированной ещё один атом расположен в центре куба. Получается сдвигом простых решеток относительно друг друга на половину диагонали. Координационное число = 8 (щелочные металлы, барий, хром. железо и др.). Гранецентрированная решетка содержит в середине каждой грани по одному атому. Координационное число = 12 (золото, серебро, медь, алюминий, свинец и др.). Такая решетка имеет более плотную упаковку атомов. Кроме этих сравнительно простых решеток, есть ещё ряд других, более сложных структур с кубической элементарной ячейкой. Наиболее важной из них является решетка типа алмаза, в которой кристаллизуются также кремний, германий и серое олово. Решетка типа алмаза представляет собой модификацию гранецентрированной решетки. Состоит из двух гранецентрированных кубических решеток, сдвинутых одна относительно другой на четверть диагонали куба. Кратчайшее расстояние меду атомами в этой решетке равно , где а – постоянная решетки, (см рис.). Эта решетка вдоль определенных направлений имеет относительно широкие каналы, что способствует внедрению примеси в глубь кристалла. Для германия и кремния а соответственно равны 0,565 и 0,542 нм, а кратчайшие расстояния между атомами 0,245 и 0,235 соответственно. Число атомов в кубическом сантиметре германия равно 4,45·10²², а кремния 5·10²². Многие полупроводниковые бинарные соединения, такие, как GaAs, InAs, ZnS, кристаллизуются в решетке типа цинковой обманки (также решетка типа алмаза, но чередуются атомы разного типа).

РЕЗЮМЕ

1. Кристаллической решеткой называется совокупность точек (узлов решетки), связанных между собой векторами трансляций

T = n₁a + n₂b + n₃c

где n₁, n₂, n₃ — целые числа, a, b, c — векторы примитивных трансляций, выбранные в качестве ортов кристаллографических осей координат.

2. Для образования кристаллической структуры с каждой точкой решетки связывается одинаковый базис, состоящий из атомов, имеющих координаты

r_j = x_ja+ y_jb + z_jc, j = 1,2, … , N.

Значения х, у, z можно подобрать таким образом, чтобы они лежали в интервале от 0 до 1.

3. Векторы примитивных трансляций a, b, c образуют ячейку минимального объема . При помощи этой ячейки, векторов трансляций Т и базиса, связанного с каждой точкой решетки, можно образовать кристаллическую структуру.

4. Иногда бывает удобнее (особенно для кубических кристаллов описывать кристаллическую структуру посредством ячейки, которая обычно выбирается таким образом, что ее объем кратен объему примитивной ячейки.

5. Положения плоскостей и направлений в кристалле обозначаются с помощью индексов Миллера hkl, которые заключаются в круглые скобки для плоскостей и в квадратные — для направлений.

6. Практически важными и довольно простыми структурами являются объемноцентрированная кубическая, гранецентрированная кубическая, гексагональная структура с плотной упаковкой, структура алмаза, структуры типа NaCl и CsCl, кубическая и гексагональная модификации кристалла ZnS.

7. В основе структуры кристаллов многих металлов и большинства полупроводниковых материалов лежат кубические решетки и их сочетания.

8. Наиболее важной из них является решетка типа алмаза, в которой кристаллизуются также кремний, германий и серое олово. Решетка типа алмаза представляет собой модификацию гранецентрированной решетки. Состоит из двух гранецентрированных кубических решеток, сдвинутых одна относительно другой на четверть диагонали куба. Кратчайшее расстояние меду атомами в этой решетке равно , где а – постоянная решетки, (см рис.). Эта решетка вдоль определенных направлений имеет относительно широкие каналы, что способствует внедрению примеси в глубь кристалла. Для германия и кремния а соответственно равны 0,565 и 0,542 нм, а кратчайшие расстояния между атомами 0,245 и 0,235 соответственно.

ЗАДАЧИ

1.1. Структура алмаза.

а) Сколько атомов содержится в примитивной ячейке алмаза?

б) Какова длина (в Аº) вектора примитивной трансляции?

в) Доказать, что угол между тетраэдрическими связями в алмазе равен 109º28’. Указание: Это угол между объемными диагоналями куба.

г) Сколько атомов содержится в примитивной гранецентрированной кубической элементарной ячейке?

1.2. Перпендикуляр к плоскости. Доказать, что в кубическом кристалле направление [hkl] перпендикулярно плоскости (hkl), имеющей те же индексы Миллера.

1.3. Коэффициент упаковки. Показать, что относительная доля объема, занимаемого твердыми шарами, моделирующими атомы, при образовании перечисленных ниже структур имеет следующие значения: для простой кубической 0,52, для объемноцентрированной кубической 0,68, для гранецентрированной кубической 0,74.

1.4. Гексагональная структура с плотной упаковкой.

а) Показать, что отношение с/а для идеальной гексагональной структуры с плотной упаковкой равно (8/3)^1/2 = 1,633. Если с/а значительно больше этого значения, то кристаллическую структуру можно рассматривать как состоящую из плотноупакованных атомных плоскостей, уложенных одна на другую довольно рыхло, неплотно.

б) Показать, что не может существовать пространственная решетка с гексагональной плотной упаковкой с базисом, состоящим из одного атома на одну точку решетки. Указание. Показать, что нельзя найти такие векторы решетки а, b, с, чтобы набор векторов трансляций Т образовал бы решетку с гексагональной плотной упаковкой. Хотя можно выбрать векторы а и b, которые образуют гексагональную сетку в базисной плоскости, однако построить пространственную решетку с гексагональной плотной упаковкой при помощи вектора с нельзя.

1.5. Кристаллические структуры. Описать гексагональные кристаллические структуры. Определить используемую кристаллическую решетку и базис.

1.6. Подрешетки. Показать, что объемноцентрированная кубическая решетка может быть разделена на две простые кубические решетки А и В так, что ни одна пара ближайших соседей исходной решетки не окажется в решетке А (и соответственно в решетке В). Показать также, что для соблюдения этого условия простая кубическая решетка должна разделиться на две гранецентрированные решетки, а гранецентрированная, в свою очередь, — на четыре простые кубические решетки. Рассмотрение этого вопроса представляет интерес для теории антиферромагнетизма.

1.7. Плотнейшая упаковка волокон. Найти плотноупакованное расположение идентичных бесконечных прямых волокон в круглом поперечном сечении. Определить коэффициент упаковки для этой системы.

1.8. Оси симметрии третьего порядка и кубические кристаллы. Показать, что кристалл, имеющий четыре оси третьего порядка, образующие попарно четырехгранные углы (см. задачу 1.1) есть кристалл с кубической решеткой. (Наличие четырех осей третьего порядка является минимальным требованием к симметрии кубического кристалла.)

1.9. Структура хлористого цезия. Выбрать за исходный ион Сs⁺ в позиции 000 в простой кубической примитивной ячейке.

а) Определить число ближайших к исходному иону соседних ионов (ионы Сl^-), затем число ионов, следующих за ближайшими (ноны Сs⁺), и, наконец, число ионов следующего, третьего «слоя» (ионы Сs⁺). Указание: Порядок в расположении соседних атомов нагляднее всего выявляется в плоскости (110). В этой плоскости находятся три главные направления, которые имеет куб: ребро куба, диагональ грани и объемная диагональ.

б) Определить координаты x, у, z всех этих ионов относительно исходного иона Сs⁺ с координатами 000.