§ 3.3. Основы квантовой теории электропроводности

Теория атома Бора

Затруднения классической физики при объяснении спектральных закономерностей при поглощении и излучении веществами энергии частично были разъяснены датским физиком Нильсом Бором в 1913 году. Его анализ проблемы атомного излучения привел к неожиданному с точки зрения физика начала XX века выводу: «ошибочно убеждение, что область применимости представлений классической физики беспредельна, она ограничена явлениями в макросистемах (L>>10^-8 см); представления классической физики неприменимы к событиям в микросистемах (атомах, молекулах), которые поэтому она не в состоянии описать».

Для объяснения совокупности известных фактов, и прежде всего фактов, касающихся строения и свойств излучаемых газами спектров, Бор предложил теорию атомов, в основу которой похожих три постулата.

Для того, чтобы объяснить устойчивость экспериментально установленной Резерфордом планетарной структуры атомов Бор допустил, что внутриатомное движение не во всем следует законам классической физики и в частности - что результаты классической электродинамики неприменимы к внутриатомным процессам.

Своеобразие атомного движения по Бору проявляется в том, что могут иметь место случаи движения заряженной частицы по замкнутым орбитам (т.е. движения заряженной частицы с ускорением), которые не будут сопровождаться излучением энергии. Наблюдения, в том числе опыты Резерфорда, указывают на такой характер внутриатомного движения. Далее, движение электронов вокруг ядра таково, что не все мыслимые траектории возможны.

Эту мысль бор выразил в форме первого постулата своей теории: «из бесконечного числа электронных орбит, возможных с точки зрения классической физики, в действительности осуществимы только некоторые определенные стационарные орбиты. При движении электрона по любой из этих орбит, несмотря на то, что он движется с ускорением, электрон, вопреки классической электродинамике, не излучает анергии.

На неизбежный вопрос, как выделить эти дискретные орбиты из числа возможных с точки зрения классической физики орбит, дает ответ второй постулат бора: «из всех возможных с точки зрения классической физики орбит в атоме осуществляются только те, для которых момент количества движения n электрона равен целому кратному величины h/2π , то есть

где n = 1, 2, 3, 4 и т.д.»

В том случае, если электрон массы m со скоростью Vn движется по круговой стационарной орбите номера n и радиуса r_n, то его момент количества движения n равен

Отсюда для круговых стационарных орбит равенство (1.38) примет вид

Анализируя спектральные закономерности атомных спектров, Бор первый понял, что комбинационный принцип отражает своеобразие законов, управляющих внутриатомными движениями. Обобщая и опираясь на идею Планка о дискретности энергетических состояний атомных вибраторов в твердом теле, он понял, что комбинационный принцип указывает на возможность для атомов и в свободном состоя­нии изменять энергии не любым образом, а только дискретно.

Эту мысль он сформулировал в третьем постулате: излучение испускается или поглощается атомом при переходе электрона из одного квантового (стационарного) состояния в другое (при квантовом скачке). Причем разность энергии этих двух состояний излучается или поглощается в виде светового кванта анергии hν).

Таким образом, воли E₁ — энергия одного стационарного состояния, а E₂, энергия другого, те при переходе атома из состояния E₂ в состояние E₁ (E₁ < E₂) излучается (поглощается, если E₁ > E₂) квант энергии

где h - постоянная Планка, ν - частота излучаемой линии.

Это состояние часто называй боровским условием частот. Оно выражает закон сохранения энергии.

С другой стороны, боровское условие частот не что иное как комбинационный принцип, выраженный иным, чем это делал В. Ритц, способом: каждая спектральная линия связана с двумя стационарными состояниями атома. Действительно, если Е₂-Е₁=hν, то

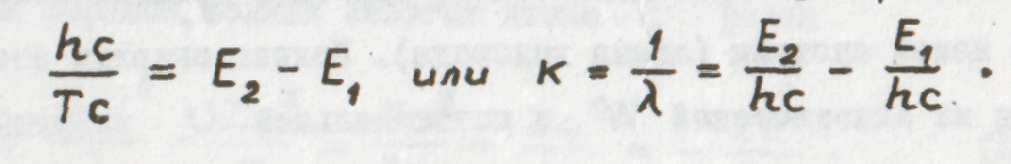
Обозначив

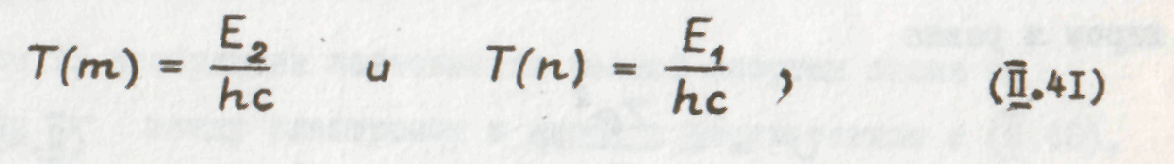
Получим

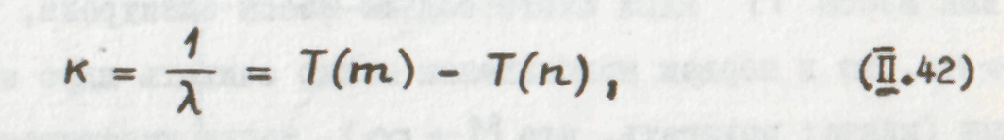
то есть известную нам аналитическую формулировку комбинационного принципа.

Таким образом, постулаты Бора по существу являются обобщением экспериментальных фактов, формулировкой на их основе характерных, специфических особенностей внутриатомного движения.

Опишем на основании теории Бора спектральные закономерности водородоподобиого атома.

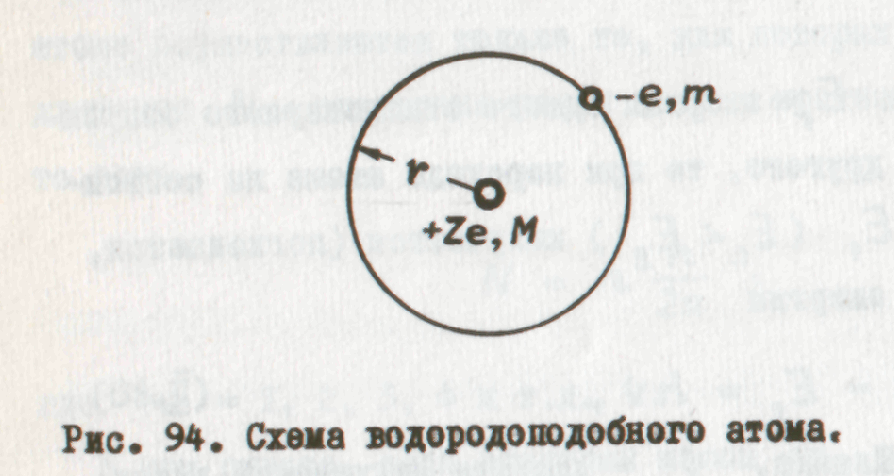
Водородоподобный атом - система, состоящая на ядра с зарядом +Ze и одного электрона (рис. 94). При Z=1 - это атом водорода, Z = 2 - однократно ионизированный атом гелия и т.д.

Взаимодействие между ядром и электроном - кулоновское. Это установили опыты Резерфорда.

Предположим, что электрон движется по круговой орбите. Вычислим энергию нашей системы (атома водорода). Полная энергия атома складывается из кинетической W и потенциальной U энергий.

Потенциальная энергия обусловлена взаимодействием электрона с ядром и равна

Так как масса М ядра много божьим массы электрона, то есть М » m, то в первом приближении можно считать ядро атома неподвижным (иначе: полагать, что М →∞), тогда кинетическая анергия системы

где V - скорость движения электрона по орбите. Следовательно, полная анергия Е будет:

Движение по криволинейной траектории есть движение о ускорением - это центростремительное ускорение электрону сообщает кулоновская сила взаимодействия его с ядром. Для этого случая движения центробежная сила компенсируется центростремительной, то есть кулоновской силой

Отсюда находится связь между кинетической и потенциальной энергиями. Сократив (П.46) на r, получим

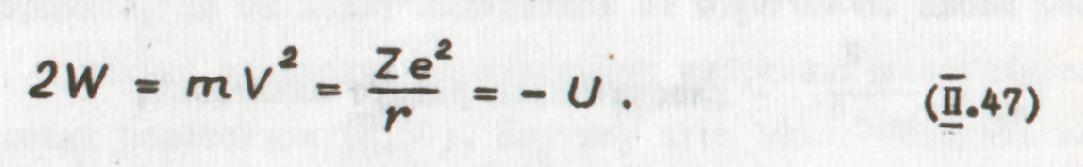
Таким образом, полная энергия атома Е равна

На рисунке 95 изображена зависимость полной энергии атома от расстояния r между электроном и ядром в соответствии с (1.48).

Теперь можно уточнять возможные энергетические состояния электрона в атоме. Так как электрон может двигаться только по стационарным орбитам, то он может находиться от ядра не на любом расстоянии, а только на вполне определенных набранных расстояниях. Поэтому атом может обладать не любой энергией, а только некоторыми разрешенными значениями ее, зависящими от числа n. Эти возможные энергетические состояния атома определяются, если в выражение (П.48) подставить значение радиусов разрешенных электронных орбит (ф-ла П.50). Это дает

Из равенства (П.55) видно, что энергия атома дискретна, изменяясь обратно пропорционально квадрату квантового числа п. С ростом п. Энергия атома растет (уменьшается ее отрицательная величина). На рис. 96 изображены эти разрешенные значения анергии.

Шимони

Зонная теория твердого тела

В дальнейшем следует учитывать, что потенциал внутри тела не постоянен, а соответствует периодичности решетки. Следовательно, вопрос в том, как ведет себя электрон в периодическом потенциальном поле согласно представлениям квантовой механики. В следующем разделе эта задача будет решена количественно. Здесь же мы хотим прежде всего добиться качественной характеристики ожидаемых результатов.

Мы начнем с рассмотрения двух различных путей: во-первых, рассмотрим, что происходит при движении свободного электрона в периодическом потенциальном поле; во-вторых, рассматривая электроны, находящиеся в связанном состоянии, исследуем, как изменяется это состояние при объединении в металле множества атомов.

В соответствии с первым способом рассмотрения проблемы плоская волна, описывающая электрон, должна двигаться в пространстве с периодическим потенциалом. Если эта волна достигнет точки кристалла, н которой потенциал меняется скачкообразно, т. е. встретится с ионом, это приведет к рассеиванию, как и в случае световой волны, которая попадает на маленькую частицу вещества. Из точки скачка потенциала, обусловленного наличием иона, исходят сферические волны по всем направлениям. В связи с тем, что ионы металла находятся в узлах правильной кристаллической решетки, интерференция сферических волн в направлении падения приводит к усилению последних; во всех других направлениях волны, напротив, ослабляются. В результате плоские волны проходят вещество без рассеивания и, следовательно, без потери интенсивности. Однако из рентгеноструктурного анализа известно, что при определенных углах падения и длинах волн обеспечиваются условия полного отражения — брэгговское отражение. Определение длины волны электрона однозначно задает величину импульса и энергии, так что электроны, обладающие определенной величиной импульса и соот­ветствующей ему величиной энергии, не могут двигаться сквозь металл. Отсюда одновременно следует, что вероятность значений, близких к этим дискретным величинам, тоже очень мала. Таким образом, видно, что энергия электрона не может принимать любое произвольное значение: наряду с разрешенными значениями энергии есть и запрещенные значения или зоны.

С помощью второго способа рассмотрения приходят качественно к такому же выводу, т. е. к тем же энергетическим зонам. Рассмотрим сначала два одинаковых атома, бесконечно удаленных друг от друга. Тогда их внешние электроны могут иметь различные энергетические уровни в соответствии с тем, что основному и возбужденным состояниям атома соответствуют различные дискретные значения энергии, которые при сближении этих атомов изменяются вследствие взаимодействия между атомами, и энергетические уровни расщепляются. Это может быть наглядно прослежено на рис. 3-28, где энергетические уровни представлены как функция расстоя­ния между атомами для случая с 8 атомами.

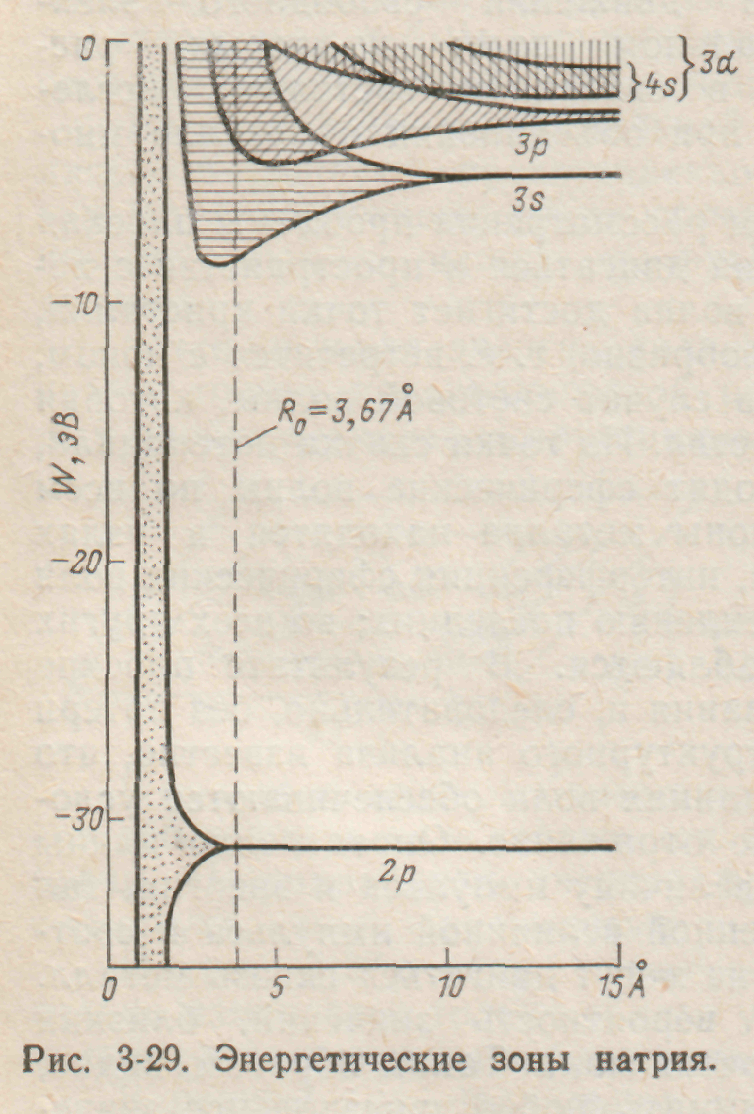
Поскольку в реальном металле очень много атомов и, кроме того, расщепленные уровни находятся очень близко друг от друга, мы получаем зоны с почти непрерывным распределением энергии (рис. 3-29).

Первоначальные дискретные энергетические уровни, расщепляясь, образуют зоны, состоящие из очень большого количества находящихся близко друг от друга энергетических уровней, на каждом из которых согласно принципу Паули могут быть размещены два электрона. Нельзя, однако, обнаружить электрон с величиной энергии, приходящейся на интервал между двумя такими зонами. Этот интервал называется запрещенной зоной. В следующем разделе будет проведено соответствующее количественное рассмотрение. После этого мы еще раз вернемся к качественному рассмотрению зонной структуры.

Электроны в периодическом потенциальном поле. Одномерный случай

Решение одномерного уравнения Шредингера. Волны Блоха.

Количественное исследование соотношений в реальном кристалле, хотя при этом предполагается идеальная (свободная от дефектов) кристаллическая структура, выглядит сложнее. При качественном рассмотрении ожидаемых соотношений одномерной кристаллической модели необходимо, чтобы ионы решетки находились на одной прямой на расстоя…….

Возможные типы зонных структур

Исходя из сказанного, рассмотрим возможные типы зонных структур в случае конкретного твердого тела. Расположим свободные атомы очень далеко один от другого, однако в соответствии с окончательной кристаллической структурой, и начнем сближать их до тех пор, пока они не займут окончательного положения равновесия. Энергетические уровни свободного атома расщепляются при этом на зоны, которые состоят из совокупности дискретных уровней. Степень расщепления зависит от взаимного расстояния атомов и может быть подсчитана с помощью методов, описанных выше. Таким образом получают энергетические зоны, изображенные на рис. 3-28???, согласно которому расщепление отдельных невозмущенных уровней молено рассматривать как функцию изменения постоянной решетки. Если рассмотреть изменение величины средней энергии от межатомного расстояния, то видно, что при совершенно определенном расстоянии между атомами она достигает минимального значения, соответствующего положению равновесия. Именно наличие этого минимума обусловливает возможность сущест­вования металлической связи. Если теперь при этом состоянии равновесия осуществить вертикальный разрез энергетической диаграммы, то получим зонную структуру металла, характерную для состояния равновесия.

С точки зрения электропроводности решающее значение имеет изучение фактической заселенности расщепленных энергетических уровней. Возьмем, например, одновалентный металл. Соответствующий s-уровень расщепляется на G³ уровней. Согласно принципу Паули на каждом энергетическом уровне может быть по два электрона с проти­воположными спинами. Всего в металле имеется G³ электронов, так что занята лишь половина возможных уровней. Не входя в детальное исследование взаимодействия электрического поля и электронов, мы знаем, что каждый электрон в случае существования электрического тока приобретает определенную энергию, передаваемую ему электрическим полем, следовательно, он должен перейти на более высокий энергетический уровень, чем тот, на котором он находился прежде. Однако это возможно лишь тогда, когда в непосредственной близости к занятым уровням есть свободный, разрешенный уровень. Это справедливо и для одновалентных металлов, о которых идет речь.

Можно было бы ожидать, что в случае с двухвалентными металлами, у которых все уровни заполнены, дальнейшее поглощение энергии электронами и, следовательно, прохождение электрического тока в металлах невозможны. Однако опыт показывает, что это не так: возбужденные уровни свободного атома также расщепляются, и обе зоны в состоянии равновесия могут перекрываться, как показано на рис. 3-38,а. Таким образом, разрешенные энергетические уровни примыкают к заполненным энергетическим уровням, минуя расположенные между ними запрещенные зоны, обеспечивая тем самым прохождение электрического тока и в двухвалентных металлах.

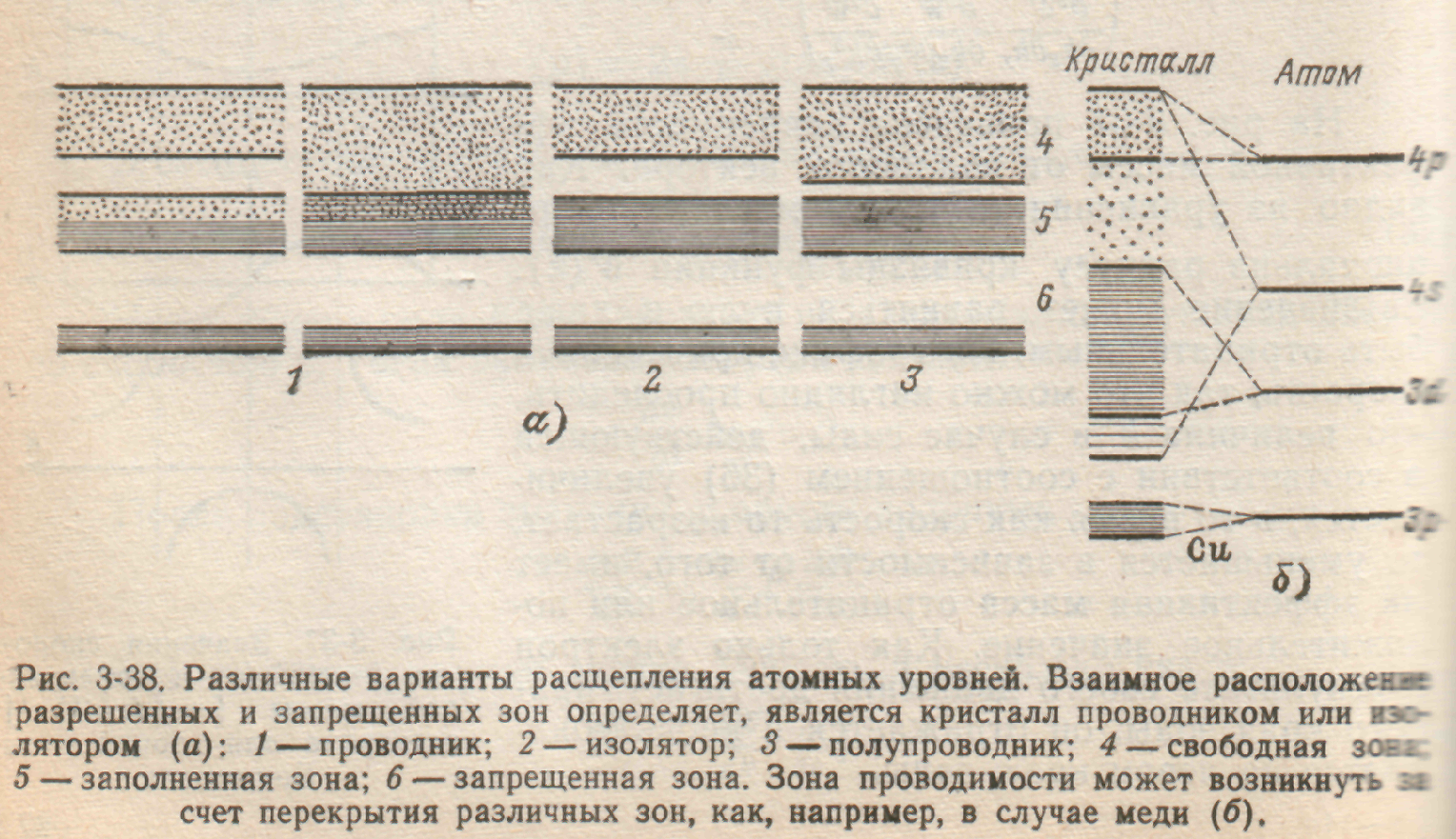
Таким образом, проводником является такое твердое тело, у которого самая верхняя зона, так называемая зона проводимости, еще не полностью заполнена электронами. Рисунок 3-38 показывает, как образуются такие не до конца заполненные зоны в проводниках, имеющих большое практическое значение. В изоляторе электронами заполнен каждый уровень этой зоны. Различные кристаллические модификации одного и того же материала могут вести себя по-разному. Если рассмотреть сильно различающиеся (рис. 3-39,а и б) расположением атомов в решетке различные модификации углерода — алмаз и графит, то окажется неудивительным, что первый является изолятором, а последний — проводником. Если заполненная зона проводимости отделена от расположенной над ней незаполненной энергетической зоны только узкой запрещенной зоной, то достаточно теплового движения электронов, чтобы забросить электроны в незаполненную зону и обеспечить, таким образом, электрическую проводимость. Такой материал — позже о чем будет сказано подробнее — называют полупроводником.

Как мы увидим в дальнейшем, перекрытие зон, а, следовательно, и сам факт, является ли твердое тело проводником, полупроводником или изолятором, определяются постоянной решетки, т. е. расстоянием между атомами, образующими решетку. Оно может быть изменено с помощью механического воздействия, что указывает, следовательно, на взаимосвязь проводимости и механических напряжений в решетке.

Опыт показывает, что в металлах концентрация электронов практически не зависит от температуры. Даже при самых низ­ких температурах в металлах уже имеется большое количество по­движных электронов. Это показывает, что в образовании электро­нов проводимости в металлах тепловое движение не играет сущест­венной роли.

Атомы типичных металлов характеризуются тем, что в них имеется один или несколько электронов, связанных с ядром слабо. При сближении атомов металла такие электроны под действием сил взаимодействия с соседними атомами отщепляются от своих атомов. Они принадлежат уже не какому-либо определенному атому, а всему металлу в целом и движутся по металлу в результирующем поле всех ионов и электронов. Эти отщепившиеся электроны н являются электронами проводимости.

Наряду с металлами мы встречаемся с проводниками и другого типа. Эти проводники являются, так же как и металлы, электронными (проводниками первого класса) и в них электрический ток не сопровождается никакими химическими изменениями. Однако концентрация носителей заряда в таких проводниках чрезвычайно сильно увеличивается с увеличением температуры. Подобные проводники при низких температурах имеют весьма большое удельное сопротивление и практически являются изоляторами, но с увеличением температуры их удельное сопротивление сильно уменьшается и при достаточно высоких температурах становится весьма малым. Вещества такого типа получили название электронных полупроводников.

Полупроводниками являются многие элементы (кремний, германий, селен и др.), закись меди Си₂О, сернистый свинец PbS и многие другие химические соединения. Так, например, по данным опыта можно заключить, что концентрация электронов в чистейшем кремнии при комнатных температурах < 10¹⁷м^-3, а его удельное сопротивление должно быть > 10³ ом·м; но при температуре 700^o С концентрация электронов в нем возрастает до 10²⁴ м^-3, а удельное сопротивление падает до 0,001 ом·м, т. е. больше чем в миллион раз.

Сильная зависимость концентрации носителей заряда в полупроводниках от температуры показывает, что в этом случае электроны проводимости возникают под действием теплового движения. В полупроводниках атомное взаимодействие само по себе еще не достаточно для отщепления электронов от атомов и превращения их в электроны проводимости. Для этого даже наиболее слабо связанным электронам нужно сообщить некоторую добавочную энергию W — энергию ионизации, которая и заимствуется из энергии теплового движения тела. Чем выше температура, тем большее число электронов будет иметь тепловую энергию, равную или превышающую W, тем большая часть электронов будет существовать в полупроводнике в отщепленном состоянии, т.е. в виде электронов проводимости.

Если величина энергии ионизации W велика по сравнению со средней энергией теплового движения (имеющей порядок kТ) при температурах в области существования данного кристалла, то электроны проводимости в заметном количестве не образуются и такой кристалл будет изолятором.

Зоны запрещенных энергий

Исходя из особенностей химической связи в полупроводниках, можно непосредственно объяснить существование запрещенной зоны энергий. Рассмотрим в качестве примера атомарные полупроводники подгруппы 1УВ и будем пока считать, что в них не имеется никаких химических примесей и структурных дефектов. Тогда из рис. 2.10 видно, что при ненарушенных связях в кристалле все валентные электроны каждого атома (два 5-электрона и два р-элек-трона) участвуют в образовании ковалентных связей. Поэтому все валентные электроны являются в известном смысле структурными элементами и находятся в связанном состоянии. В таком состоянии (температура абсолютного нуля и отсутствие внешних ионизующих воздействий) кристалл является изолятором.

Для создания подвижных электронов необходим разрыв некото­рого количества связей. Это происходит при повышении темпера­туры и под действием подходящих ионизующих излучений (свет, быстрые электроны и т. п.). При разрыве каждой связи возникает один электрон проводимости и одно вакантное квантовое состояние электрона. Наименьшее приращение энергии электрона при его переходе из связанного состояния в состояние проводимости (работа разрыва связи) есть ширина запрещенной зоны энергий Е_й.

Если в полупроводнике имеется электрическое поле, то элек-1 троны проводимости будут двигаться против поля, и возникнет электронный ток с некоторой плотностью ]„. Однако, кроме этого процесса, возможен еще и другой механизм электропроводности. А именно, при нарушенных валентных связях (наличие вакантных мест) какой-либо из электронов связи может перейти в одну из этих вакансий. В результате на месте вакансии будет восстановлена нормальная ковалентная связь, но зато появится вакансия в другом месте. На эту вакансию в свою очередь может перейти какой-либо другой из электронов связи и т. д. При этом, разумеется, возможны переходы электронов связи во всех направлениях. Однако переходы в направлении действующей силы (против поля) будут преимущест­венными, и поэтому возникнет некоторый дополнительный ток \_р, обусловленный перемещением электронов связи. Сами же вакансии будут перемещаться в направлении поля, т. е. так, как двигались бы положительно заряженные частицы. Этот второй механизм электропроводности и есть процесс дырочной проводимости. Сам;. же вакантные квантовые состояния электронов, локализованные у нарушенных ковалентных связей и способные перемещаться по; действием поля, суть положительные дырки. Из сказанного ясно, что в беспримесном полупроводнике концентрация дырок р всегда равна концентрации электронов проводимости п. В гл. IV будет показано, что именно для дырок (а не для электронов связи) полу­чаются простые уравнения движения, аналогичные уравнения-движения положительно заряженных частиц в классической меха­нике, чем и оправдывается введение этого понятия.

Эти представления о механизме дырочной проводимости, рас­смотренные нами качественно на примере полупроводников подгруппы 1УВ, справедливы для полупроводников любого типа

Движение электрона в идеальном кристалле, имеющем минимум энергии в зоне проводимости при к = 0 и максимум на границе зоны Бриллюэна при к = к_d представляется следующим образом. Под действием силы внешнего электрического поля электрон, обладающий наименьшей энергией, будет ускоряться и, следовательно, увеличивать свою энергию. При этом волновой вектор электрона будет возрастать, устремляясь к значению к = к_d. Однако вблизи края зоны Бриллюэна эффективная масса электрона становится отрицательной, что приведёт к торможению электрона и возвратному движению в исходное положение. Таким образом, под действием внешнего поля электрон в идеальном кристалле должен совершать колебательные движения.

В реальных кристаллах поведение электрона совершенно иное. Эта разница в поведении обусловлена большим количеством содержащихся в реальных кристаллах дефектов и колебаниями решетки. Поэтому за время, необходимое электрону для того, чтобы значение его волнового вектора ощутимым образом возросло под действием поля, электрон успевает много раз столкнуться с дефектами решетки и колеблющимися атомами. Обычно при каждом столкновении электрон полностью отдает кристаллической решетке накопленную в электрическом поле энергию. В результате средняя накопленная энергия при не очень сильных электрических полях не может быть значительной и оказывается существенно меньше средней тепловой энергии электрона.

Среднее для всех электронов значение волнового вектора в не очень сильных полях не изменяется значительным образом. Однако в каждом отдельном акте столкновения значение волнового вектора отдельно взятого электрона сильно изменяется. В то же время, как было отмечено выше, количество энергии, отдаваемой электроном кристаллической решетке при каждом соударении, ничтожно мала. Следовательно, волновой вектор электрона при столкновении заметно изменяется лишь по направлению, а не по абсолютному значению, оставаясь практически на одной и той же изоэнергетической поверхности в к-пространстве. Такие соударения электрона называются упругими.

Таким образом, поведение электрона в реальных кристаллах при воздействии электрического поля представляется в следующем виде. На хаотическое тепловое движение электрона накладывается направленный дрейф в электрическом поле, причем средняя энергия электрона, накопленная в электрическом поле, а следовательно, и дрейфовая скорость его оказываются значительно меньше соответствующих тепловых параметров. Действительная длина пути, пройденного электроном, значительно больше пути дрейфа по направлению поля.

Процесс накопления энергии электроном в электрическом поле сопровождается перераспределением электронов по энергетическому спектру, в результате чего функция распределения электронов f(Е) становится неравновесной и отличной от равновесной функции f₀(Е) Максвелла — Больцмана или Ферми — Дирака. Переход в равновесное состояние функции распределения после выключения внешнего поля, очевидно, происходит в результате столкновений электронов, т.е. посредством их рассеяния. Поскольку отклонение от равновесного состояния невелико, то обычно полагают, что скорость возвращения функции распределения в исходное состояние пропорциональна величине отклонения:

где τ — некоторое время релаксации. Решением (8.1), чевидно, является выражение

В течение времени τ разность f—f₀ уменьшается в е раз по сравнению с первоначальным значением. Следовательно, время релаксации характеризует стремление частиц прийти к равновесию. Анализ показывает [21, что время релаксации равно среднему времени свободного пробега электрона между двумя столкновениями. Кроме указанного параметра, для описания процессов переноса вводят понятие о средней длине свободного пробега l=υτ, где υ — полная скорость электрона.

Если предположить, что в результате соударения полностью теряется приобретенная, до этого дрейфовая скорость, то среднюю скорость дрейфа электрона можно выразить как:

где qEτ/m_n* представляет собой ускорение электрона во внешнем электрическом поле Е. Знак минус указывает на то, что скорость электрона направлена в противоположную сторону по отношению к направлению напряженности поля. Равенство (8.3) обычно записывают в виде

где μ_n - подвижность электрона, т.е. величина скорости дрейфа, обусловленная полем с напряженностью, равной единице. Нетрудно видеть, что подвижность, равная

учитывает влияние рассеяния носителей на их перенос. Аналогичная формула в случае полупроводников может быть написана и для дырок:

Оценим дрейфовую и тепловую скорость электрона и время релаксации, например, для германия. В чистом германии при комнатной температуре μ_n = .3900 см²/(в·сек). Полагая эффективную массу электрона в германии равной 0,3 m, получим из (8.5) время релаксации τ == 6·10^-13 сек. Известно, что тепловая скорость электрона в кристалле, определяемая из условия

при комнатной температуре равна υ_т ≈2,5·10⁷ см/сек. Дрейфовая скорость электрона в германии при Е = 1 в/см равна 3,9·10³ см/сек, т. е. примерно на четыре порядка меньше, чем тепловая скорость. Интересно отметить, что длина свободного пробега электрона в рассмотренных условиях составляет l≈1,5·10^-5 см, что в сотни раз больше межатомных расстояний в^: кристалле.

Рассмотрим далее выражение для электропроводности кристалла. Положим, что время релаксации τ не зависит от скорости электрона, т.е. от его энергии или волнового вектора. При таком предположении все свободные электроны независимо от их расположения в энергетическом спектре имеют дрейфовую скорость, описываемую формулой.

Каждый электрон, летящий в электрическом поле с дрейфовой скоростью υ_n, создает электрический ток — qυ_n. Плотность тока в кристалле, содержащем n электронов в единице объема, очевидно, равна

или, подставляя (8.3), получим

С другой стороны, электропроводность образца σ определяется равенством

Сопоставляя (8.9) и (8.10), получим выражение для электропроводности кристалла:

или

Нетрудно видеть, что электропроводность кристалла пропорциональна концентрации носителей заряда и среднему времени свободного пробега (времени релаксации) или соответственно длине свободного пробега.

Если в кристалле, помимо электронов, содержатся дырки, то плотность тока вместо (8.8) будет выражаться формулой

где υ_р — дрейфовая скорость дырок. Тогда, очевидно, выражение для электропроводности кристалла запишется так:

Полученное выражение широко используется, когда известны из экспериментальных исследований значения подвижностей носителей заряда.

Если кристалл имеет изоэнергетическую поверхность в виде сферы, то полученные выражения для электропроводности справедливы для любого направления тока и поля в кристалле. Однако, если изоэнергетическая поверхность имеет более сложный вид, то электропроводность становится анизотропной. Действительно, поскольку эффективные массы электрона m₁, m₂, m₃, соответствующие главным осям эллипсоида, различны, то различными будут также и подвижности электрона в соответствующих направлениях:

Как было показано, большинство кристаллов имеют не один, а несколько эквивалентных минимумов энергии, расположенных в различных направлениях волнового вектора, причем в каждом из трех основных направлений решетки три главные оси эллипсоидов чередуются. Поэтому в таких кристаллах электропроводность усредняется и становится вновь изотропной:

где величину

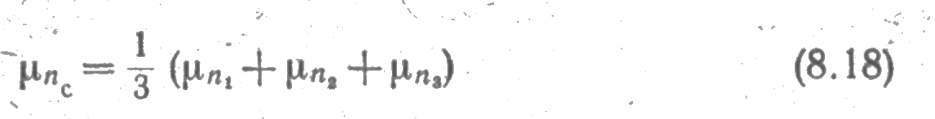
можно назвать «омической» подвижностью. Омическая подвижность связана с омической массой m_c* определяемой формулой (6.62), следующим соотношением:

В кристаллах с кубической симметрией изоэнергетические поверхности имеют вид эллипсоидов вращения. Если зона Бриллюэна такого кристалла, содержит лишь один минимум энергии, то электропроводность будет носить анизотропный характер. В этом случае в соответствии с составляющими эффективной массы продольная и поперечная составляющие подвижности будут равны:

Примером полупроводника с таким типом анизотропии электропроводности может служить теллур, у которого поперечная составляющая электропроводности σ_т почти вдвое больше продольной составляющей σ_L. Однако если в кристалле происходит усреднение подвижности электронов по всем изоэнергетическим эллипсоидам зоны Бриллюэна, то электропроводность становится изотропной и описывается выражением (8.17), а омическая подвижность дается формулой

Электропроводность с учетом зависимости τ(υ)

Рассмотренные выше соотношения не учитывали зависимости времени релаксации от скорости или соответственно энергии и волнового вектора частиц. Фактически же скорость частиц, основную часть которой при слабых полях составляет тепловая скорость; существенно влияет на время релаксации. Учет этой зависимости может быть осуществлен усреднением времени релаксации по всевозможным скоростям частиц [23].

Рассмотрим электропроводность с учетом зависимости τ(υ) применительно к невырожденному кристаллу со сферическими изоэнергетическими поверхностями. Как уже было отмечено выше, приложенное к образцу электрическое поле приводит к отклонению функции распределения от равновесного значения. Поскольку это отклонение при не очень сильных электрических полях невелико, то неравновесную, функцию можно разложить в ряд около равновесного значения и ограничиться двумя членами ряда:

где f₀(Е) – равновесная функция распределения Ферми-Дирака или Максвелла-Больцмана.

…………..

Окончательное выражение для плотности тока:

Электропроводность кристалла и подвижность носителей в этом случае соответственно равны:

Таким образом, если известен характер зависимости времени релаксации от энергии τ(Е), то, подставив эту зависимость в (8.37), найдем усредненное время релаксации и электропроводность кристалла.

Электропроводность вырожденного полупроводника

Для вырожденного полупроводника уже нельзя пользоваться классической равновесной функцией распределения, а все рассмотрение, начиная с выражения (8.25), необходимо проводить аналогично с применением функции Ферми — Дирака.

При очень сильном вырождении полупроводника или в случае металла расчет электропроводности несколько упрощается, благодаря тому, что функция распределения имеет почти ступенчатый вид. В интеграле (8.25), содержащем производную df₀/dE, в случае сильного вырождения основную роль играет лишь область значений энергий вблизи Е_ф. При этом все сомножители подынтегральной функции в выражении для плотности тока можно вынести за знак интеграла как относительно медленно меняющиеся функции. Таким образом, после преобразований получим:

Используя (8.41), после соответствующих преобразований, получим

Из этой формулы видно, что все электроны в зоне проводимости сильно вырожденного полупроводника или металла как бы участвуют в электропроводности с одним и тем же .временем релаксации, соответствующим электронам, находящимся вблизи уровня Ферми. Физический смысл формулы (8.42) заключается в том, что в процессе релаксации непосредственное, участие могут принимать лишь только те электроны, энергия которых близка к Е_ф. Поэтому существенную роль играют только те значения времени релаксации, которые соответствуют энергиям вблизи Е_ф. Иными словами, заметные отклонения неравновесной функции распределения, вызывающее появление тока, от своего равновесного положения наблюдаются лишь вблизи уровня Ферми. Следовательно, участвуют в создании электрического тока лишь электроны, расположенные вблизи уровня Ферми. Это обусловлено тем, что лишь эти электроны имеют возможность рассеиваться и совершать случайные переходы в ближайшие свободные состояния.

…….

Изложенные соображения позволяют глубже понять, почему в случае полностью заполненной зоны отсутствует электропроводность. Действительно, в такой зоне нет свободных от электронов состояний, в которые могли бы переходить электроны в процессе накопления энергии и в результате рассеяния. Отсутствует также возможность систематического перемешивания электронов в зоне.

Если поверхности постоянной энергии не обладают сферической симметрией, а, например, представляют собой эллипсоиды, то электропроводность будет величиной анизотропной, причем составляющие подвижности выражаются формулой (8.15), а вместо τ подставляется соответствующее усредненное время релаксации.

Механизмы рассеяния и подвижность свободных носителей заряда

Полученные в предыдущем параграфе формулы для электропроводности в зависимости от времени релаксации не могут быть использованы, пока не будет установлена конкретная зависимость времени релаксации от энергии τ(Е) и произведено соответствующее усреднение. В свою очередь характер зависимости времени релаксации от энергии существенным образом зависит от конкретного механизма рассеяния. Центры рассеяния, т. е. объекты, с которыми могут взаимодействовать (соударяться) свободные носители заряда, могут иметь самую различную природу. Соответственно в реальном кристалле насчитывается сравнительно много различных механизмов рассеяния свободных носителей, каждый из которых дает свою зависимость τ(Е). Наиболее существенными механизмами: рассеяния являются: рассеяние на тепловых колебаниях решетки, на ионизированных и нейтральных атомах примеси, рассеяние на дислокациях, рассеяние в результате электрон-электронного взаимодействия и другие. Результирующее время релаксации и соответствующая подвижность носителей определяются совокупным действием указанных механизмов рассеяния.

Электропроводность полупроводников

Собственная электропроводность

Остановимся подробнее па процессе образования электронов проводимости в полупроводниках. Для конкретности дальнейших рассуждений рассмотрим кремнии, являющийся типичным полупроводником.

Атом кремния имеет порядковый номер в периодической системе Менделеева Z=14. Поэтому заряд ядра атома кремния равен +14е и в состав его атома входит 14 электронов. Однако из них только четыре являются слабо связанными. Именно эти слабо связанные электроны участвуют в химических реакциях и обусловливают четыре валентности кремния, отчего они и получили название валентных электронов. Остальные десять электронов вместе с ядром составляют остов атома, имеющий заряд +14е—10е = +4е. Он окружен четырьмя валентными электронами, которые движутся вокруг остова и образуют облако отрицательного заряда (рис. 316).

В решетке кремния расположение атомов таково, что каждый атом окружен четырьмя ближайшими соседями. Упрощенная плоская схема расположения его атомов показана на рис.317.

Связь двух соседних атомов обусловлена парой электронов, образующих так называемую парно-электронную, или валентную, связь.

Картина, изображенная на рис. 317, соответствует чистому кремнию (о влиянии примесей будет сказано ниже) и очень низкой температуре. В этом случае все валентные электроны участвуют в образовании связей между атомами, являются структурными элементами и не участвуют в электропроводности.

При повышении температуры кристалла тепловые колебания решетки приводят к разрыву некоторых валентных связей. В результате этого часть электронов, ранее участвовавших в образовании валентных связей, отщепляется и становится электронами проводимости. При наличии электрического поля они перемещаются против поля и образуют электрический ток.

Однако, кроме процесса переноса заряда с помощью электронов проводимости, возможен еще и другой механизм электропроводности. Он обусловлен тем, что всякий разрыв разрыв валентной связи приводит к появлению вакантного места с отсутствующей связью. Такие «пустые» места с отсутствующими электронами связи получили название «дырок» (рис. 318).

Легко видеть, что возникновение дырок в кристалле полупроводника создает дополнительную возможность для переноса заряда. Действительно, при наличии дырки какой-либо из электронов связи может перейти на место дырки. В результате на этом месте будет восстановлена нормальная связь, но зато появится дырка в другом месте. В эту новую дырку в свою очередь сможет перейти какой-либо из других электронов связи и т. д. Такой процесс будет происходить многократно, в результате чего в образовании тока будут принимать участие не только электроны проводимости, но и электроны связи, которые будут постепенно перемещаться, так же как и электроны проводимости, против электрического поля. Сами же дырки будут двигаться противоположно, в направлении электрического поля, т. е. так, как двигались бы положительно заряженные частицы (рис. 319).

Рассмотренный процесс получил название дырочной проводимости. Следовательно, в полупроводниках возможны два различных процесса электропроводности: электронный, осуществляемый движением электронов проводимости, и дырочный, обусловленный движением дырок.

На первый взгляд может показаться, что представление об электропроводности с помощью дырок является весьма искусственным и даже неоправданным, так как дырки, т. е. «пустые» места, естественно, не могут переносить электрический заряд, а в действительности, как мы видели, перенос заряда осуществляется перемещением электронов связи. Дело, однако, заключается в том, что движение электронов, как уже упоминалось выше, подчиняется законам не классической, а квантовой механики. А законы квантовой механики показывают, что если только концентрация дырок мала по сравнению с концентрацией электронов связи, то простые законы движения получаются лишь для дырок, но не для электронов связи. А именно, оказывается, что дырки в электрических и магнитных полях движутся так же, как двигались бы положительно заряженные частицы, обладающие зарядом +е и некоторой определенной массой (вообще не равной массе электрона). Поэтому и все электрические процессы при наличии дырок происходят так, как если бы наряду с отрицательными электронами проводимости имелись еще и положительно заряженные частицы - дырки.

Наряду с переходами электронов из связанного состояния в свободное существуют обратные переходы, при которых электрон проводимости улавливается на одно из вакантных мест электронов связи. Этот процесс называют рекомбинацией электрона и дырки. В состоянии равновесия устанавливается такая концентрация электронов (и равная ей концентрация дырок), при которой число прямых и обратных переходов и единицу времени ниш одинаково.

Рассмотренный процесс проводимости и совершенно чистых полупроводниках, лишенных вовсе химических примесей и других дефектов решетки, получил название собственной проводимости.

Примесная электропроводность полупроводников

При наличии примесей электропроводность полупроводников сильно изменяется. Укажем в качестве примера, что кремний с добавкой фосфора в количестве всего около 0,001 атомного процента имеет удельное сопротивление при комнатной температуре около 0,006 ом·м, т.е. его сопротивление уменьшается более чем в 100 000 раз по сравнению с совершенно чистыми кристаллами.

Такое влияние примесей вполне объясняется изложенными выше представлениями о строении полупроводников. Вернемся опять к конкретному примеру кремния и предположим, что в нем имеются атомы химической примеси, замещающие некоторые атомы кремния. В качестве примеси рассмотрим сначала какой-либо элемент пятой группы, например мышьяк. Атом мышьяка как элемент пятой группы имеет пять валентных электронов. Но для осуществления парно-электронных связей в решетке кремния, как мы видели, необходимы всего четыре электрона. Поэтому пятый электрон атома мышьяка оказывается связанным особенно слабо и может быть легко отщеплен при тепловых колебаниях решетки. При этом возникает один электрон проводимости, а атом мышьяка превращается в положительно заряженный ион. Образование же дырки не происходит. Подобный процесс схематически изображен на рис. 320, а.

Посмотрим теперь, как будет вести себя атом примеси какого-либо элемента, стоящего левее в периодической системе, нежели кремний; пусть это будет бор, стоящий в третьей группе. Атом бора имеет всего три валентных электрона, в то время как для нормальной валентной связи в решетке кремния необходимы четыре электрона. Недостающий четвертый электрон будет захвачен из соседних мест кристалла, в соответствующем месте образуется дырка, а атом бора превратится в отрицательный ион (рис. 320, а). Таким образом, и при наличии бора в кристалле кремния окажется возмож­ным возникновение тока, но, в отличие от случая мышьяка, электрический ток здесь будет обусловлен движением дырок, а не электронов.

Следовательно, электропроводность полупроводников может быть обусловлена также примесями (примесная проводимость). Примеси, вызывающие появление электронов проводимости (например, мышьяк в кремнии), получили название донорных примесей, а примеси, вызывающие появление дырок (например, бор в кремнии), названы акцепторными.

Резюмируя сказанное, мы видим, что полупроводники обладают той особенностью, что электропроводность в них может быть обусловлена как подвижными электронами, так и дырками. Если концентрация электронов в полупроводнике значительно больше кон­центрации дырок, то мы говорим, что полупроводник имеет электронную проводимость, или проводимость n-типа (от negativ — отрицательный). Если же значительно преобладают положительные дырки, то электропроводность называется дырочной, или p – типа (от pozitiv — положительный). Носители заряда, представленные в большинстве (электроны в полупроводнике n-типа и дырки в полупроводнике p-типа), получили название основных носителей заряда, а представленные в меньшинстве — неосновных. Если же концентрации электронов и дырок сравнимы между собой, то мы имеем смешанную проводимость.

Так, например, кремний с примесью мышьяка при низких температурах имеет только примесную проводимость и является полупроводником n-типа. Основные носители заряда в нем — электроны, а неосновные — дырки. Последние возникают лишь в результате разрыва валентных связей и их количество при низких температурах мало. Но при увеличении температуры количество таких процессов увеличивается и появляется заметная собственная проводимость. При этом увеличивается и количество дырок, и электропроводность по типу делается смешанной. При достаточно высоких температурах примесная проводимость, напротив, делается гораздо меньше, нежели собственная, и концентрация дырок становится практически равной концентрации электронов.

Неравновесные электроны и дырки в полупроводниках

Рассмотрим опять контакт двух полупроводников р- и n-типа и предположим, что через него идет ток в проходном направлении (рис. 434). Дырки в р-области движутся к р-n-переходу и, проходя через него, вступают в n-область в качестве неосновных носителей заряда, где и рекомбинируют с электронами. То же относится и к электронам в n-области, которые, переходя границу раздела, попадают в р-область и рекомбинируют с дырками. Однако эта рекомбинация происходит не мгновенно, и поэтому в n-области окажется избыточная концентрация дырок n_д, а в р-области — избыточная концентрация электронов n_э. При этом избыточные дырки в n-области будут притягивать к себе электроны, так что увеличится и концентрация электронов; объемный заряд, как и в отсутствии тока, не обра­зуется. То же будет происходить и в р-области, где увеличение концентрации электронов повлечет за собой увеличение концентрации дырок.

Таким образом, при наличии электрического тока через р-n-переход состояние электронов и дырок в полупроводнике становится неравновесным. Их концентрация делается больше ее равновесного значения, происходит как бы «впрыскивание» дырок в n-область и электронов в р-область. Описанное явление получило название инжекции электронов и дырок.

Отметим, что нарушение равновесного состояния электронов и дырок можно также получить под действием освещения полупроводника, даже если последний и однороден. В этом случае изменение концентрации электронов и дырок приводит к изменению электропроводности полупроводника под действием света (явление фотопроводимости).

По мере движения избыточные дырки и электроны будут рекомбинировать и их концентрация будет уменьшаться. Поэтому распределение концентраций избыточных электронов и дырок в кристалле существенно зависит от скорости их рекомбинации. Остановимся на этом вопросе подробнее.

Положим, что в полупроводнике каким-либо способом (инжекцией, освещением или другим) была создана концентрация избыточных электронов и дырок n₀, одинаковая во всех местах кристалла, и что эти избыточные носители заряда исчезают вследствие рекомбинации. Уменьшение концентрации электронов или дырок —dп за время dt пропорционально избыточной их концентрации n и времени:

Здесь 1/τ коэффициент пропорциональности, определяющий вероятность рекомбинации, а величина τ получила название среднего времени жизни избыточных (или неравновесных) носителей заряда. Она зависит от рода и качества материала, от его состояния и от содержащихся в нем примесей. Интегрируя написанное уравнение, находим:

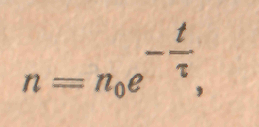
где n₀ — начальная концентрация избыточных носителей. Отсюда видно, что τ есть такое время, через которое концентрация неравновесных носителей вследствие рекомбинации уменьшается в e = 2,71 раза.

Пользуясь понятием времени жизни, мы можем сейчас вернуться к распределению электронов и дырок в пространстве (рис. 434). Для этого рассмотрим в правой части кристалла (n-области) бесконечно тонкий слой, ограниченный плоскостями, параллельными р-n-переходу и удаленными от него на расстояния х и (х+dx).

Через каждую единицу поверхности плоскости х в единицу времени вследствие диффузии внутрь слоя будет входить число ды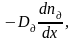рок где D_д — коэффициент диффузии дырок и n-области. Через плоскость (х+dх) будет выходить из слоя число дырок Поэтому полное приращение количества дырок за единицу времени вследствие диффузии, отнесенное к единице объема, равно + . Кроме этого внутри слоя будет происходить уменьшение числа дырок вследствие рекомбинации. Согласно сказанному выше число исчезающих дырок в единицу времени, также отнесенное к единице объема, есть В стационарном состоянии количество поступающих дырок вследствие диффузии должно быть равно числу дырок, исчезающих вследствие рекомбинации. Поэтому для определения пространственного распределения концентрации избыточных дырок (и равной ей концентрации избыточных электронов) в n-области мы получаем уравнение

где введено обозначение:

Граничные условия задачи имеют следующий вид. При х=0 п_д=п_д0, где п_д0 — концентрация избыточных дырок вблизи перехода. Кроме этого при х→∞ п_д→0, так как на достаточно большом расстоянии от перехода все избыточные дырки успевают рекомбинировать с электронами.

Решение написанного уравнения, удовлетворяющее граничным условиям, имеет вид:

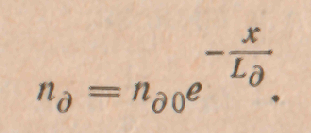
Оно показывает, что концентрация инжектированных дырок затухает с увеличением расстояния от перехода по экспоненциальному закону. Введенная нами характеристическая длина L_д, есть расстояние, на котором концентрация избыточных дырок уменьшается в е = 2,71 раза. Величина L_д носит название длины диффузионного смещения или, короче, длины диффузии дырок.

Совершенно аналогично концентрация инжектированных электронов в р-области будет тоже уменьшаться по экспоненциальному закону, но будет определяться длиной диффузии электронов где D_э — коэффициент диффузии электронов, а τ_э— время жизни электронов в p-области.

Укажем для примера, что в очень чистом германии при комнатных температурах τ может достигать нескольких миллисекунд, что соответствует L в несколько мм. При наличии примесей (или иных структурных дефектов) τ и L могут уменьшаться на много порядков,