Порядок виконання практичної роботи:
Завдання 1
Розв'язати задачу Коші:
,
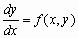y (0)
= 1 з кроком
h =
0.1 на
відрізку
[0, 1]:
методом Ейлера;
використовуючи функцію rkfixed
використовуючи функцію Rkadapt..
Побудувати графіки функцій в одній системі координат, отриманих методом Ейлера та за допомогою функцій rkfixed та Rkadapt..
№ |
f(x, y) |
№ |
f(x, y) |
№ |
f(x, y) |
1 |
x + y |
6 |
2 y - cos 2 x |
11 |
2 y + 3 e - x |
2 |
2 x 2 + 2 y |
7 |
y - e x / 2 + 2 |
12 |
y / 2 - e - x |
3 |
e x - 3 y |
8 |
3 y - 2 sin x |
13 |
y + (cos x) /3 |
4 |
y - sin x |
9 |
e 2 x - y |
14 |
y - 4 x + 5 |
5 |
y / 3 - x 2 |
10 |
2 sin x + y |
15 |
2 x - y / 3 - e x |
Завдання 2. Розв'язати задачу Коші для системи ОДУ при заданих початкових умовах на відрізку [0, 2] c кроком h = 0.2 за допомогою функції rkfixed. Побудувати графіки функцій u(t) і v(t).
№
|
Система |
Початкові умови |
№
|
Система |
Початкові умови |
||||||
|
u(0) |
u’(0) |
v(0) |
v’(0) |
|
u(0) |
u’(0) |
v(0) |
v’(0) |
||
1 |
|
1.5 |
1.5 |
1 |
1 |
9 |
|
2 |
0 |
-1 |
1 |
2 |
|
-1 |
1 |
-1.5 |
3 |
10 |
|
-1 |
2 |
-1.5 |
0 |
3 |
|
1.5 |
1.5 |
1 |
1 |
11 |
|
1.5 |
1.5 |
-1 |
-1 |
4 |
|
1 |
1.5 |
0 |
2 |
12 |
|
-1 |
1.5 |
0 |
-2 |
5 |
|
0.5 |
1.5 |
-1 |
2 |
13 |
|
-0.5 |
1 |
-1 |
2 |
6 |
|
0.5 |
2 |
1 |
2 |
14 |
|
0 |
-2 |
0 |
2 |
7 |
|
5 |
5 |
-1 |
1 |
15 |
|
3 |
3 |
-1 |
1 |
8 |
|
1.5 |
1 |
3 |
1 |
|
|
|
|
|
|
Завдання
3. На відрізку
[a, b] с використанням
функцій load, score и
sbval перетворити краєву
задачу:
=
f(x, y, y’) при граничних
умовах y(a)
= А, y(b) = В до
задачі Коші
і знайти
розв’язок заданного
дифрівняння в 10 проміжних
точках за допомогою
функції rkfixed.
№ варианта |
f(x, y, y’) |
Граничные условия |
|||
|
a |
b |
y(a) |
y(b) |
|
1 |
ex y + cos x |
1 |
2 |
0 |
0 |
2 |
y sin x + e -x |
2 |
3 |
1 |
0 |
3 |
y cos x + tg x |
0 |
1 |
0 |
0.45 |
4 |
x3 y + cos x |
0 |
1 |
1 |
0 |
5 |
x + ex y/(1 - x) |
2 |
4 |
1 |
0.14 |
6 |
x2 y + 1/(1 + x) |
1 |
3 |
0 |
0.17 |
7 |
y cos x + cos 2x |
1 |
2 |
0 |
0 |
8 |
(2 + x) y + arctg x |
0 |
3 |
0 |
0.22 |
9 |
(5 - x) y + x |
2 |
4 |
0 |
-1.2 |
10 |
e -x y + 2 e -x |
0 |
1.5 |
2.4 |
0 |
11 |
e -x y/x + x |
-3 |
-2 |
3 |
0 |
12 |
(x2 + 1/x) y + 1/x 2 |
2 |
3 |
0 |
0 |
13 |
(10 - x) y + x |
-1 |
0 |
2 |
0 |
14 |
y/x2 + x |
1 |
3 |
1.5 |
0 |
15 |
y ln x + 1 + x |
7 |
8 |
0 |
0 |
Завдання 4
Розв'язати диференціальне рівняння вищого порядку, використовуючи функцію rkfixed і функцію Rkadapt. Побудувати графіки знайденої функції та її похідних в одних осях.
№ Вар. |
Завдання |
Початкові умови |
|||||
X1 |
X2 |
Y(x1) |
Y'(x1) |
Y''(x1) |
|||
|
|
|
2 |
5 |
1 |
-2 |
|
|
|
|
|
0 |
2.0 |
4.0 |
-3.0 |
|
|
|
|
|
1.0 |
3.0 |
-1.0 |
0 |
|
|
|
|
|
0 |
1.0 |
0 |
0 |
|
|
|
|
|
0 |
2.0 |
3.0 |
-1.0 |
1.0 |
|
|
|
|
0 |
2.0 |
0 |
-3.0 |
3.0 |
|
|
|
|
1.0 |
2.0 |
1.0 |
-2.0 |
|
|
|
|
|
2.0 |
3.0 |
1.0 |
-2.0 |
|
|
|
|
|
2.0 |
3.0 |
1.0 |
-2.0 |
|
|
|
|
|
2.0 |
10.0 |
1.0 |
-2.0 |
|
|
|
|
|
8.0 |
10.0 |
1.0 |
-2.0 |
|
|
|
|
|
2.0 |
3.0 |
1.0 |
-2.0 |
|
|
|
|
|
1.0 |
3.0 |
1.0 |
-2.0 |
|
|
|
|
|
1.0 |
3.0 |
1.0 |
-2.0 |
|
|
|
|
|
1.0 |
3.0 |
1.0 |
-2.0 |
|
|
