27.Система в симметричном виде. Построение интегралов.

Симметрическая форма системы дифференциальных уравнений

Для нахождения интегрируемых комбинаций при решении системы дифференциальных уравнений иногда бывает удобно записать ее в симметричной форме

(18)

В системе дифференциальных уравнений, записанной в симметрической форме, переменные   равноправны, что в некоторых случаях упрощает нахождение интегрируемых комбинаций. Для решения системы (18) либо берут пары отношений, допускающие разделение переменных, либо же используют производные пропорции

где коэффициенты   производные и их выбирают так, чтобы числитель был дифференциалом знаменателя, либо равен нулю. Пример. Найти общее решение системы уравнений

Решение. Первая интегрируемая комбинация  . Разделяя переменные и интегрируя, найдем первый интеграл Вторую интегрируемую комбинацию получим, используя производные пропорции (19). Для этого сложим числители и знаменатели дробей системы (20):

здесь  . Отсюда  , или   и, значит,

Первые интегралы (21) и (22) дают общий интеграл системы (20)

из которого находим общее решение системы

28. Непрерывная зависимость решений от параметров и начальных данных. Если правая часть дифференциального уравнения   (1) непрерывна по λ при   и удовлетворяет условиям теоремы Пикара, причём постоянная Липшица не зависит от λ, то решение y = y(x, λ) (2) уравнения (1), удовлетворяющего условию  непрерывно зависит от λ.

Доказательство. Аналогично доказательству теоремы Пикара.  (3), при  .

Тем же методом можно показать непрерывную зависимость решения  уравнения   от начальных значений  . При этом только уменьшается h

Вопрос о непрерывной зависимости решения от начальных данных сводится к вопросу о непрерывной зависимости решения от параметра. Сделаем замену:  z=y( )- (4), t=x- .

Тогда уравне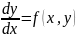ние  ,  переходит в уравнение   (5), к которому уже можно применить теорему о непрерывной зависимости решения от параметров  (f удовлетворяет условиям теоремы Пикара).

Непрерывная зависимость от начальных данных, т. е. y( ) , где   (или  ) означает, что для  Что из неравенств  Следует, что 

С возрастанием b число  , как правило, уменьшается.

Особый интерес вызывает решение, которое мало изменяется при произвольном, но малом изменении начальных значений для сколь угодно больших значений аргумента. Такое решение называется устойчивым.

29. Свойства решений линейной однородной системы.

Линейные однородные системы дифференциальных уравнений (ЛОС ДУ). ЛОС ДУ для функции y(x), z(x) называется система уравнений вида (3.1)

где - непрерывные на (a,b) функции. Свойства решений ЛОС ДУ (3.1).

1. Сумма двух решений системы (3.1) – тоже решение этой системы.

Доказательство: Пусть – два каких-либо решения системы (3.1). Тогда

Но и . Аналогично рассматривается и второе уравнение системы (3.1).

2. Если y(x), z(x) – решение ЛОС ДУ и c – произвольная константа, то cy(x), cz(x) – тоже решение (3.1). Доказательство свойства аналогично доказательству свойства 1.

Следствие. Если и - решения системы (3.1), то выражение вида где - произвольные постоянные, тоже решение (3.1).

Определение 1. Система функций и называется линейно независимой на некотором интервале (a,b), если из системы равенств (3.2) Следует, что В противном случае система функций и - линейно зависима на (a,b). Определение 2. Определитель, составленный для системы функций и называется определителем Вронского и обозначается W(x). Итак .

Теорема 1. Определитель Вронского для линейно независимой на интервале (a,b) системы решений и 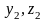ЛОС ДУ не равен нулю ни в одной точке (a,b). Доказательство. Докажем теорему методом от противного. Предположим, что существует точка , в которой

Составим линейную однородную систему уравнений с неизвестными  и  : (3.3)

Так как определитель системы (3.3) равен нулю, то система имеет бесконечное множество ненулевых решений. Пусть - одно из них. С помощью этих констант и двух линейно независимых на (a,b) решений системы (3.1) и составим две функции (3.4)

Согласно следствию из свойств решений ЛОС ДУ функции (3.4) являются решениями системы (3.1), которые в силу (3.3) в точке обращаются в нуль. Следовательно, y(x), z(x) – решение следующей задачи Коши: Но таким решением может быть только нулевое решение: y(x)=0, z(x)=0 при , т.е. 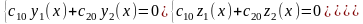Причем 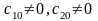. Это означает, что система функций и линейно зависима на (a,b), что противоречит условию теоремы. Значит наше предположение о существовании на (a,b) точки , в которой , неверно, что и доказывает теорему.

Определение 2. Линейно независимые на (a,b) решения ЛОС ДУ и называются фундаментальной системой решений системы (3.1).

Теорема 2. Если семейство функций и образует фундаментальную систему решений ЛОС ДУ (3.1), то их линейная комбинация , (3.5) где - произвольные постоянные, дает общее решение системы (3.1) Доказательство.

1. Выражение (3.5), согласно следствию из свойств решений ЛОС ДУ, является решением системы уравнений (3.1).

2. Докажем, что (3.5) – общее решение (3.1), т.е. докажем, что каковы бы ни были начальные условия задачи Коши, всегда найдутся значения постоянных такие, что выделенное из общего частное решение ЛОС ДУ: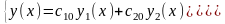

будет удовлетворять этим условиям. Для этого подставим в (3.5) начальные условия: 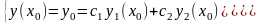(3.6)

Определителем этой алгебраической системы линейных уравнений является определитель Вронского

который, согласно теореме 1, не равен нулю. Следовательно, система уравнений (3.6) имеет решение и притом единственное.