9. Просторове квантування

Р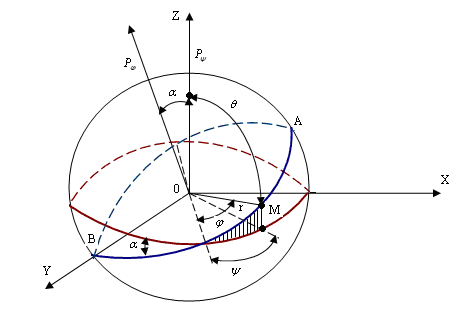 ух електрона в просторі і його положення характеризується трьома координатами, і є рухом з трьома степенями вільності. В сферичній системі координат ( , , ) відповідно до умов Зоммерфельда ми отримаємо три рівняння, які описуватимуть рух з трьома степенями вільності:

(2.54)

Тут - радіальне квантове число

- екваторіальне квантове число

- широтне квантове число

Тут кут між віссю Z і електроном (в точці М), який рухається по еліптичній орбіті АВ, яка складає кут з площиною (XOY).

Якщо на систему не діють зовнішні сили, то орбіта руху електрона буде нерухомою і плоскою. Визначимо величини інтегралів руху, які входять в рівняння (2.54). Вираз для кінетичної енергії має вигляд (для сферичної системи координат):

(2.55)

А повна енергія буде як сума кінетичної і потенціальної:

(2.56)

Або через функцію Гамельтона:

Тоді для величин імпульсів маємо:

(2.57)

Враховуючи, що без дії зовнішніх сил, повна енергія системи визначається головним квантовим числом, то отримаємо:

n=n_r+n_θ+n_ψ=n_r+n_φ (2.58)

n_θ+n_ψ=n_φ

В вираз повної енергії системи координата не входить, отже:

або

Тоді на основі третьої умови квантування в (2.54) маємо:

(2.59)

Величина являє собою проекцію повного моменту кількості руху електрона на вісь Z. Позначимо , тоді ;

Враховуючи, що та n_θ+n_ψ=n_φ, то значення квантового числа може бути в межах:

(2.60)

приймає (2 n_φ+1) [ =0; 1; 2… ] значень

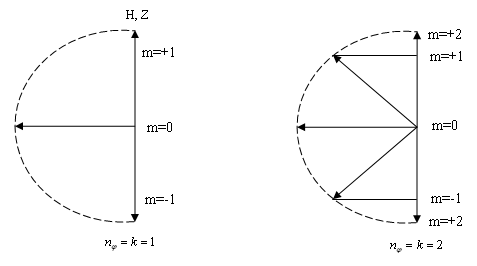
- магнітне квантове число, так як воно визначає проекцію магнітного і механічного моментів на напрямок зовнішнього магнітного поля. Отримаємо ще більш значне виродження системи по ,(раніше було тільки по =К, азимутальному).

Накладання магнітного поля знімає виродження по . Орбіти руху електрона з різним значенням будуть мати в такому випадку різні енергії. Визначимо орієнтації механічного моменту в магнітному полі:

10. Магнетон Бора

Електрон, що рухається по орбіті, еквівалентний контуру зі струмом. Сила цього струму і рівна заряду електрона е, помноженому на число його обертів в 1 секунду

(2.61)

А площа, осягнена струмом і, рівна площі еліпса S.

Для моменту кількості руху , який визначений добутком маси електрона на подвоєну секторну швидкість , повинна виконуватись умова:

(2.62)

Звідси , К – азимут кв. числа.

Але за другим законом Кеплера секторна швидкість =const = ,

Тоді:

(2.63)

Магнітний момент контуру зі струмом дорівнює:

Підставляючи отримані значення i та S маємо:

(2.64) (2.65)

Це магнетон Бора.

Магнітні моменти атомів, обумовлені орбітальним рухом електрона, повинні бути кратні елементарному магнітному моменту.

Для перевірки висновків теорії просторового квантування і експериментального визначення величини магнетона Бора був проведений дослід Штерна і Герлаха (1922р.).

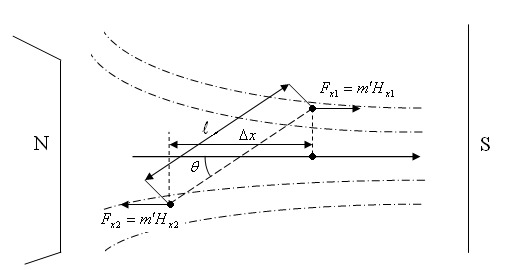
Ідея досліду. Якщо в неоднорідному магнітному полі напрямленому по осі х, розміщений магнітний диполь довжиною l , вісь якого утворює кут з напрямком поля, то сила (виштовхувальна), яка діє на диполь буде рівна:

(2.56)

Де - величина «магнітної маси», яка зосереджена на кожному з полюсів диполя, але , і тоді заміняючи l через магнітний момент диполя маємо:

(2.67)

Цей вираз буде справедливий і тоді, коли магнітний момент створюється не тільки «магнітними масами», а і струмом, який протікає по контуру, чи рухом електрона по орбіті атома.

Отже, якщо пропускати через таке неоднорідне поле атоми речовини, то вони повинні відхилятися від напрямку свого початкового руху, і це відхилення буде проходити по різним закономірностям з точки зору класичних і квантових уявлень.