8. Еліптичні орбіти в атомі водню і їх квантування

При русі по колу міняється одна координата – азимут φ або пройдений шлях, , тобто є одна ступінь свободи. Такий рух характеризується одним постійним параметром - радіусом r = const, який в класичній механіці може мати будь-яке значення 0 < r < ∞, відповідно будь-яке значення можуть мати інші параметри, що характеризують рух (енергія Е, момент кількості руху mvz і т.д.) Встановлена раніше умова механічної стійкості ( ) дає тільки певний зв'язок між різними параметрами:

(2.33)

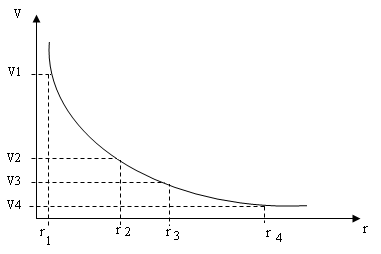
Залежність v та r представлена графіком, тут же на осях v та r відмічені квантові значення v та r, одержувані згідно теорії Бора для атома водню з урахуванням його другого і третього постулату, коли

(2.34)

(2.35)

Отже квантові умови другого постулату Бору

(2.36)

виділяють з неперервної нескінченої множини кругових орбіт дискретну нескінченну множину.

Проте електрон може рухатися не тільки по колу, але і по еліптичній орбіті, в одному з фокусів якої буде ядро (1-й закон Кеплера). В цьому випадку змінними є два параметри - азимут φ і відстань електрона до ядра – r (тобто дві степені свободи), а траєкторія руху характеризується двома постійними параметрами - малою (а ) і великою (b ) піввіссями еліпса, які згідно класичній механіці можуть приймати будь-які значення:

0 < b < ∞ та 0 < а < ∞ .

Отже, сукупність можливих рухів - двояко-нескінченна неперервна множина. При цьому класична механіка вимагає виконання двох законів Кеплера

(2.37)

Чи можна узагальнити другий постулат Бора і проквантувати еліптичні орбіти електрона в одноелектронних системах, тобто виділити з двояко-нескінченної неперервної множини деяк двояко-нескінченну, але дискретну множину?

Однієї квантової умови недостатньо, дійсно, спробуємо використати лише умову, що

(2.38)

то цій умові задовольняє різноманіття орбіт, для яких (2-38) встановлює тільки залежні від п зв'язки між а і b еліпса, тобто b = f_n(a) , але величина а може бути довільною. Тобто в системі з f степенями свободи квантування вимагає f квантових умов. Опишемо таку систему узагальненими координатами g_i і узагальненими імпульсами p_i, де (і = 1,2,3. f) . Якщо позначити К ( g_і, ġ_і ) - кінетичну енергію, тоді

, тут = - узагальнена швидкість.

Умови квантування атома по Зоммерфельду вимагає, щоб інтеграли рухів( величини, не змінні з часом) для стаціонарних квантових рухів мали дискретні значення, кратні постійній Планка

(2.39)

інтегрування в межах (від 0 до 2π або від min до max ). Коло на інтегралі означає, що інтегрування по координаті g_і треба проводити по всьому циклу її змін.

= 0, ± 1; ± 2…

Вираз (2.39) і виділяє з неперервної нескінченої множини рухів, можливих по класичній механіці, деяку дискретну множину. Наприклад, для кругового руху єдиною узагальненою координатою буде азимут φ; g₁ = φ, тоді кінетична енергія через узагальнену швидкість приймає значення , а спряженний з координатою узагальнений імпульс буде

,

тобто просто момент кількості руху, який повинен бути квантований, умова Зоммерфельда запишеться у вигляді:

(2.40)

але згідно другому закону Кеплера mrv = const, тоді (2-40) має вигляд:

або , де = 1,2,3…

Виходить, що другий постулат Бору є окремий випадок умов квантування Зоммерфельда.

При русі електрона по еліптичній орбіті за узагальнені координати треба взяти r і φ. Тоді його повна кінетична енергія має значення , а спряжені імпульси будуть визначатись як

і

тоді умови Зоммерфельда запишуться:

(2.41)

(2.42)

Де n_r та n_φ радіальні та азимутальні квантові числа. Враховуючи, що mrv=const маємо:

(2.43)

Тобто, як і для руху по колу, але тут r_n = r_n(t) і v_n=v_n(t). (2.43) визначає момент кількості руху електрона в атомі.

Використовуючи рівняння (2.41) і (2.42) з врахуванням законів Кеплера можна визначити значення великих та малих піввісей еліпса та повну енергію системи E_nφ,nr, які відповідають певним парам значень n_φ n_r . Дані величини мають вигляд:

(2.44)

(2.45)

(2.46)

Тут - радіус першої Боровської колової орбіти і V_i – іонізаційний потенціал даної системи.

Враховуючи, що a b, то з (2.44) і (2.45) випливає, що або 0, тобто

=0,1,2,3, (2.47)

При b=0 - еліпс вироджується в пряму, яка проходить через ядро,що неможливо. Отже,

=1,2,3,… (2.48)

В рівняння виходить сума =n – головне квантове число, а азимутальне число позначимо символом k, тоді n=1,2,3… k=1,2,3…n, але

(2.49)

З врахуванням позначень n і k для a, b і E маємо:

; ; (2.50)

Розглянемо можливі орбіти руху електрона, в залежності від значення головного квантового числа n:

n	1	2		3			4
k	1	2	1	3	2	1	4	3	2	1
a	a0	4 a0	4 a0	9 a0	9 a0	9 a0	16 a0	16 a0	16 a0	16 a0
b	a0	4 a0	2 a0	9 a0	6 a0	3 a0	16 a0	12 a0	8 a0	4 a0

А діаграма енергетичних рівнів для одно електронної системи буде мати наступний вигляд:

Стан з різним k позначаються: S, P, D, F…

Із діаграми видно, що хоча число квантових типів руху зросло, але число рівнів енергії залишилось, і це зрозуміло з (2.50), адже і не залежить від азимутального числа =k. Але це означає, що при різних типах руху, енергія системи залишається постійною.

Незалежність енергії системи від якого-небудь квантового числа називається «виродженням» енергії по даному квантовому числу.

Слід відмітити, що є рух при якому періоди зміни координат r і однакові, тобто еліпс нерухомий в просторі, як показав Зоммерфельд це можливо при виконанні двох умов:

1. Електрон рухається в чисто Кулонівському полі, коли ≈ .

2. І при постійній масі електрона.

Але з врахуванням залежності маси електрона від швидкості розрахунки Зоммерфельда показали, що періоди зміни r і не співпадають і еліпс буде змінювати своє положення в просторі, тоді траєкторія електрона буде мати більш складний вигляд.

Тоді для значення енергії атома в даному стані зі значенням квантових чисел =n і =k буде більш складне рівняння (по Зоммерфельду):

, (2.51)

де - постійна тонкої структури

По (2.51) залежить від n і k, тобто виродження по азимутальному квантовому числу вже ліквідовано. Але така ліквідація виродження має приводити до ускладнення спектра випромінювання атома водню, так як одному енергетичному рівню з головним квантовим числом n будуть відповідати різні енергії, які визначаються різними значеннями =k, тобто буде система підрівнів – тонка структура спектра. Розглянемо першу лінію серії Бальмера, яка відповідає переходу з рівня n=3 на рівень n=2. З врахуванням азимутального квантового числа для n=3 → k= =1,2,3- тобто маємо третій трьох квантовий (3S,3P,3D) рівень і перехід на другий двоквантовий рівень (2s,2p): (k=1,2)

Отже, перша лінія Бальмера повинна складатися з групи шести близько розташованих ліній, але в експерименті завжди спостерігається менше ліній.

Аналіз спектрів показав, що в них є тільки ті лінії, які відповідають переходам між рівнями, для яких виконується умова:

(2.52),

Всі решта переходів малоймовірні.

Тоді для першої лінії Бальмера залишаться тільки три лінії, які відповідають переходам:

1) 3S→2P

2) 3P→3S

3) 3D→2P

Правило переходів між рівнями яке визначається виразом (2.52) і називається правилом відбору.