Рівняння Шредінга (1887 – 1961, (австр. Фізик)

В 1926 р. Шредінгер, виходячи з ідеї де Бройля про хвильові властивості матерії розробив теорію руху мікрочастинок – хвильову механіку, в основу якої покладено рівняння Шредінгера, що грає в атомних процесах таку саму фундаментальну роль, як і закон Ньютона в класичній механиці. Шредінгер руху мікрочастинки поставив у відповідність комплексну функцію координат і часу, яка відома нам як хвильова функція або “псі-функція”, вид якої одержується з рішення рівняння Шредінгера наступного типу:

, (4.24)

де m – маса частинок, Δ – оператор Лапласа, U – функція часу і координат. У цьому рівнянні . При русі частинки в стаціонарному силовому полі, функція U не залежить явно від часу і має зміст потенціальної енергії. В такому випадку Ψ-функцію можна отримати з більш простого рівняння:

,(4.25)

де Е – повна енергія частинки ( ). (4.25) називаається рівнянням Шредінгера для стаціонарних станів, його частіше записують у вигляді:

(4.26)

Рівняння Шредінгера являється основним рівнянням і не виводиться з яких-небудь міркувань, справедливість його доводиться тим, що всі наслідки, що витікають з нього точно узгоджуються з дослідними фактами. Розглянемо, як можна не вивести, а прийти до рівняння Шредінгера на прикладі одномірного випадку руху частинки, що рухається вільно, якій ми співставляємо по Луї де Бройлю плоску хвилю типа (4.17)

, (4.17)

Якщо продиференціювати (4.17) один раз по t, а другий раз двічі по х, то отримаємо

,

звідси

, .(4.27)

У нерелятивістській класичній механиці маємо зв’язок між W_k (кінетичною енергією) і P(імпульсом) у вигляді , підставляючи сюди вираз для E і P з (4.27) отримаємо після скорочення на Ψ рівняння:

, (4.28)

яке співпадає з рівнянням (4.24) при U=0. При русі частинки в силовому полі, що характеризується потенціальною енергією U, повна енергія ( ) і Р зв’язаний з кінетичною енергією співвідношенням , підставивши в цей вираз E і P з (4.27), отримаємо:

.(4.29)

Множемо (4.29) на Ψ і переносимо доданок в ліву частину. Отримаємо рівняння:

, (4.30)

яке співпідає з (4.24).

Якщо в рівнянні (4.25) функцію U розглядати як оператор (оператор – це правило, за допомогою якого одній функції ставиться у відповідність інша функція)

і ввести інший оператор , рівний сумі операторів ( ) і U, тоді рівнянню (4.30) можна придати вигляд:

(4.31)

де оператор називають гамільтоніаном, який являється оператором енергії.

• Зміст Ψ-функції.

Правильну інтрепрітацію Ψ-функції дав М. Борн (нім. фізик, 1882 – 1970) у 1926 р. Згідно Борну квадрат модуля Ψ-функції визначає густину ймовірності, тобто ймовірність віднесену до одиниці об’єму, виявлення частинки в відповідному місті простору в даний момент часу. Якщо густина ймовірності відмінна від нуля в обмеженому об’ємі dV, тоді інтеграл від добутку Ψ-функції на її комплексно-спряжену по даному об’єму має дорівнювати 1:

. (4.32)

Умова (4.32) називається умовою нормування, а Ψ-функції, що задовільняють даній умові – нормованими. Отже, квантова механіка має чисто статистичний характер і дає можливість передбачати ймовірність виявлення частинки в різних точках простору.

Найпростіші приклади рішення рівняння Шредінгера

У рівняння Шредінгера в якості параметра входить повна енергія частинки Е. В теорії диференціальних рівнянь доводиться, що рівняння типу мають рішення не при любих значеннях Е, а тільки при деяких вибраних, що називаються власними значеннями даного параметра. Рішення, що відповідають власним значенням Е, називаються власними функціями даної задачі. Знайдем власне значення енергії Е і власні функції, що їм відповідають, для декількох задач.

1. Частинка в одномірній потенціальній ямі.

П рипустимо, що частинка може рухатися тільки вздовж вісі х, при цьому рух обмежений непроникними стінами, коли для х<0 і х>l U=∞, а для 0≤х≤ l U=0. Визначемо енергію частинки в такій ямі, тобто знайдемо власні значенні даного параметра і власні функції Ψ(х). Застосовуємо рівняння Шредінгера в вигляді (4.15) з врахуванням, що випадок одномірний:

. (4.33)

Згідно умови, частинки за межами х<0 і х>l нема, відповідно , тоді з врахуванням того, що в цій області, де маємо з (4.33):

. (4.34)

Вводимо позначення

(4.35)

Отримаємо рівняння

(4.36)

Його рішення має вигляд:

або

(4.37)

Використовуємо граничні умови (4.34) і підставляємо їх у рішення (4.37), в результаті отримаємо:

що можливо тільки при

. (4.38)

З рівнянь (4.35) і (4.38) знаходимо власні значення енергії частинки:

,(4.39)

тобто отримаємо квантовані значення енергії частинки, причому значення енергії дуже сильно залежать від розміру потенціальної ями . Наприклад: електрон у ямі розміром l 1см, m = 9,110^-28г.

.

Для різниці енергій маємо , тобто практично суцільний спектр, а не дискретний спектр енергій. Але при розмиірах потенціальної ями порядка атома, коли l 10^-7см, ми отримаємо . Тут відстані між рівнями вже є суттєво дискретними. Для знаходження власних функцій необхідно визначити значення амплітуди y -функції, що можна зробити, використовуючи умову нормування хвильових функцій. У нас . Тоді умова нормування дає

.

Згідно умови, підінтегральна функція на кінцях проміжку інтегрування перетворюється в нуль, тоді значення інтеграла отримується як добуток середнього значення на l, тобто звідси . Отже, власні функції мають значення:

(4.40)

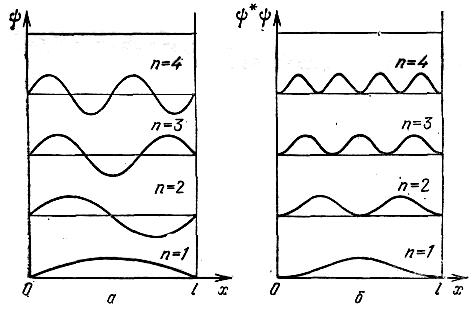
Графік цих функцій має вигляд а), а для густини ймовірності виявлення частинки на різних відстанях від стінок ями має вигляд б). З графіка випливає, що в стані з n=2, частинка не може бути виявлена на середині ями, хоча однаково часто буває як в лівій так і в правій частинах, тобто частинка траєкторії не має (згідно класичної фізики положення частинки рівноймовірно).