Особливості методу Лагранжа-Ейлера для розв’язання оберненої задачі динаміки

Цей метод ґрунтується на рівнянні Лагранжа наступного вигляду:

(3.4)

де L – функція Лагранжа (L = T – V); T – кінетична енергія системи; V – потенціальна енергія; q_i – узагальнені координати ; - узагальнені сили та моменти.

Рух кожної ланки маніпулятора описується в системі координат з шістьма вимірами , де - вектор початку координат кожної ланки, та , ,  - кути Ейлера. Вони пов’язують n-у cсистему координат досліджуваної ланки з базовою . Отже, узагальнені координати будуть такими:

or ,

де t – час.

Необхідно відмітити, що однозначне розв’язання оберненої задачі динаміки можливе тільки для маніпулятора з 6 степенями свободи, тобто N = 6.

Особливості використання розподілення мас та тензора інерції

Якщо розглядається обертання, то необхідно знати розподілення маси по всіх осях обертання. Тоді використовується тензор інерції:

,

де для робота з дискретним розподіленням маси справедливо наступне:

(3.5)

(3.6)

а для робота з неперервним розподіленням маси справедливо таке:

де - густина ланки.

Швидкість ланки

Нехай вектор визначає положення точки P відносно базової системи координат (x₀, y₀, z₀). Вектор буде визначати положення тієї ж точки, але вже в i-й системі координат (рис. 3.6). Таким чином, швидкість точки P в базовій системі координат може бути визначена як .

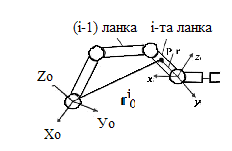
Рис. 3.6. Геометрія двохмірного маніпулятора

Тепер час згадати, що вектор може бути записаний через перетворення Денавіта-Хартенберга наступним чином:

Таким чином, можна отримати:

,

де q_i – незалежні змінні _i. Останній вираз може бути переписаний як

. (3.7)

Тепер можна показати, що

, (3.8)

де Q_i – постійні матриці. Наприклад, для будемо мати

Отже, для обертальних зчленувань матриця Q_i буде та для призматичних зчленувань матриця Q_i буде зовсім простою .

Тепер визначимо величину D_ij як . Нарешті, можна легко записати похідні більш високих порядків

(3.9)

Кінетична енергія маніпулятора

Кінетична енергія dT системи з масою dm дорівнює

де dT_i – кінетична енергія i-ої ланки маніпулятора. Вона може бути знайдена з наступного виразу:

(3.10)

де позначення ‘tr’ відповідає оператору сліду матриці, тобто, сумі діагональних елементів матриці.

Тепер розглянемо добуток у дужках:

.

Тоді вираз (3.10) можна переписати як:

Про інтегрувавши обидві частини цього виразу, отримаємо:

Інтегральна складова у дужках є матрицею інерції і-ої ланки відносно початку координат і-ої системи координат:

Виразимо величину J_i через складові тензора інерції I наступним чином:

(3.11)

де - координати центра мас і-ої ланки в і-ій системі координат. Таким чином, сумарна кінетична енергія маніпулятора дорівнює

.

Потенціальна енергія маніпулятора

Сумарна потенціальна енергія V маніпулятора, яка залежить від ваги робота, також може бути визначена як сума потенціальних енергій всіх ланок:

,

де - вектор положення центра мас і-ої ланки в і-ій системі координат, g – прискорення сили тяжіння.