Особливості перетворення Денавіта – Хартенберга при розв’язанні задач кінематики

Перетворення Денавіта – Хартенберга описує системи координат ланок маніпулятора з n степенями свободи. Перехід між системами координат сусідніх ланок здійснюється матрицею однорідних перетворень 4x4.

Перша система координат зв’язана з базою та вважається однорідною [x₀ y₀ z₀ 1]^T. Її початок координат приймається за нульове зчленування. Перетворення Денавіта – Хартенберга представляє взаємне положення всіх ланок маніпулятора за допомогою чотирьох характеристик: a, , d,  (рис. 3.1). Тут d_i – відстань між ланками, _і – кут зчленування, a_i – довжина ланки, _і – кут скручування ланки. У загальному випадку параметри a_i та _і є константами та залежать від конструкції маніпулятора.

Отже, можна отримати представлення точки r_i, що описана в i-тій системі координат, через r_i-1 шляхом таки перетворень:

1) обертання навколо осі Z_i-1 на кут _i таким чином, щоб осі x_i-1 та x_i стали паралельними: R(Z_i-1, _і);

2) перенесення вздовж осі Z_i-1 на відстань d_i таким чином, щоб сумістити осі x_i-1 та x_i: T(Z_i-1, d_i);

3) перенесення вздовж осі x_i на відстань a_i таким чином, щоб сумістити початки координат двох систем координат: T(x_i, a_i);

4) обертання навколо осі x_i на кут _і таким чином, щоб сумістити початки координат двох систем координат: R(x_і, _і).

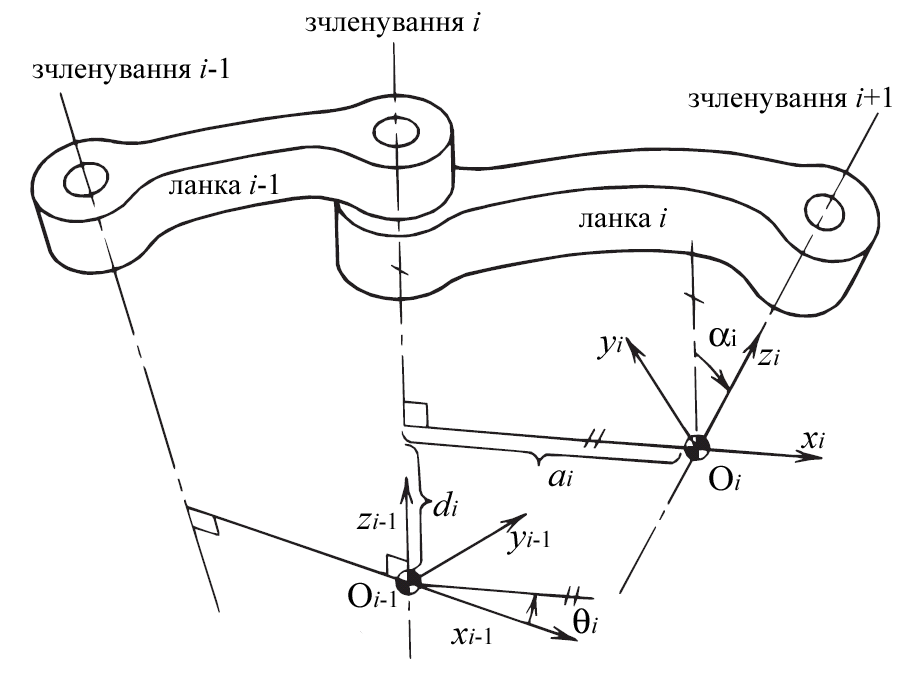
Рис. 3.1. Перетворення Денавіта-Хартенберга

Таким чином, повне перетворення, що зв’язує і-ту ланку з (і–1)-ою або і-те зчленування з (і – 1)-м, має такий вигляд:

(3.1)

Потім можна перейти від (і – 1 )-ої ланки до і-тої ланки шляхом виконання наступної операції: r_i-1=A_i-1 r_i, де - вектори координат точки в і-тій та (і – 1)-ій системі координат.

Алгоритм перетворення Денавіта-Хартенберга

1. Визначте базову систему координат [x₀y₀z₀] таким чином, щоб вісь z₀ співпадала з віссю руху першого зчленування.

2. Повторіть те саме для всіх зчленувань. Це значить, що вісь Z_i завжди буде паралельна осі поступального руху або обертання (i+1) зчленування.

3. Визначте початок координат i-ої системи координата бо як перетин осей Z_i та Z_i-1, або як перетин осі Z_i зі спільною нормаллю до осей Z_i та Z_i-1.

4. Визначте вісь x_i в кожному i-му зчленуванні як перпендикуляр до осей Z_i та Z_i-1.

5. Визначте вісь y_i таким чином, щоб утворилася правостороння система координат.

6. Знайдіть d_i як відстань від початку координат (і – 1)-ої системи координат до точки перетину осей Z_i-1 та x_i.

7. Знайдіть a_i як відстань між точкою перетину осі Z_i-1 зі спільною нормаллю до осей Z_i-1 та Z_i та початком координат i-ої системи координат.

8. Знайдіть кут _і як кут обертання від осі x_i-1 до осі x_i .

9. Знайдіть кут _і як кут обертання від осі Z_i-1 до осі Z_i відносно осі x_i .

Обернена задача кінематики заключається в знаходженні вектора переміщень зчленувань , якщо задано бажані положення та орієнтація захоплювача. Положення та орієнтація захоплювача задаються як правило у вигляді матриці T однорідних кінематичних перетворень, яка описує положення та орієнтацію системи координат захоплювача 0UVW відносно базової системи координат 0XYZ наступним чином:

, (3.2)

що включає матрицю направляючих косинусів та вектор положення початку системи координат [p_x p_y p_z]^T (рис. 3.2, a, б).

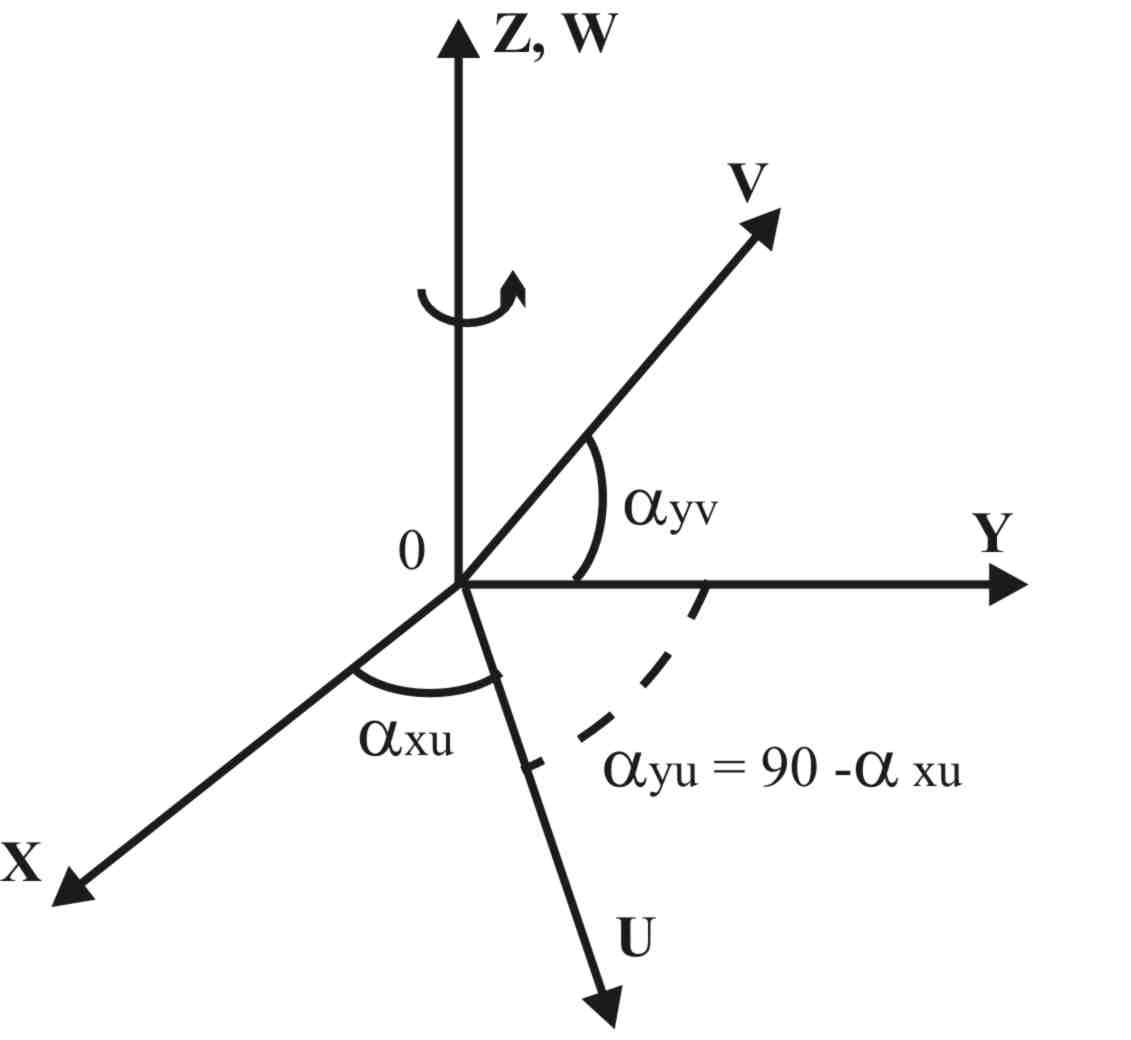
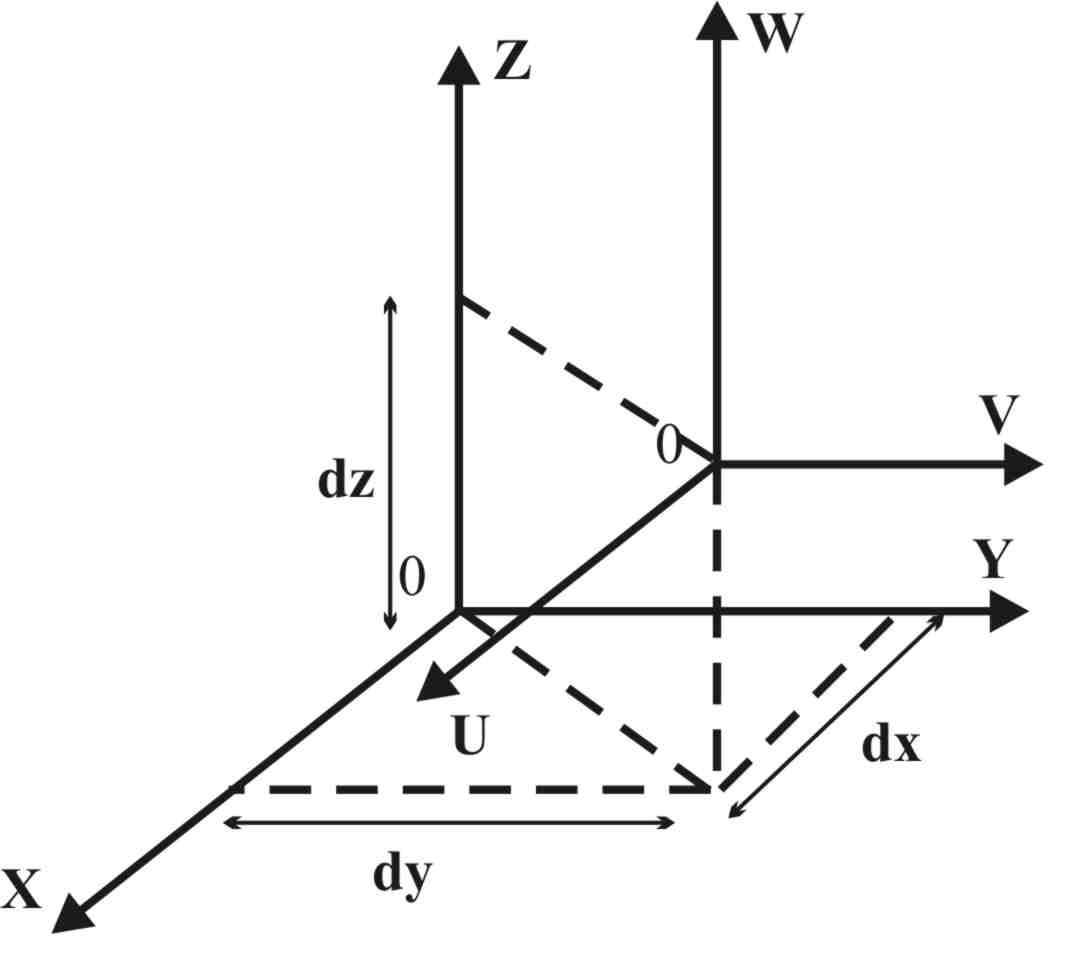
a б

Рис. 3.2. Взаємозв’язок між системою координат захоплювача та базовою системою координат