2.2. Задания для самостоятельного решения

Задача 1. Составить программу, которая по введенному значению аргумента вычисляет значение функции:

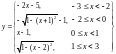
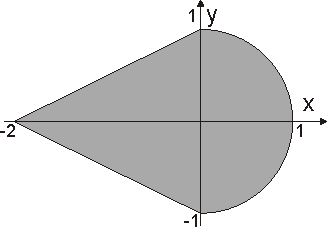
Задача 2. Даны действительные числа х и у. Определить, принадлежит ли точка с координатами (х, у) выделенной на рис. части плоскости.

Задача 3. Даны действительные положительные числа х, у, z. Выяснить, существует ли треугольник с длинами сторон х, у, z и, если треугольник существует, то определить его вид по углам.

Треугольник существует, если его наибольшая сторона меньше суммы двух других сторон. После ввода длин сторон большую из них необходимо определить через переменную max. Но значение какой переменной х, у или z будет хранить промежуточная переменная max, и с суммой какой пары сторон её сравнивать? В этом случае условие существования треугольника запишется так: . Действительно, если, например, у – наибольшая сторона, то имеем: .

Аналогичное выражение можно рассмотреть и для записи условий, определяющих вид треугольника по углам. Пусть у - наибольшая сторона треугольника. Тогда , а по следствию из теоремы косинусов:

Знак числителя в правой части этого равенства совпадает со знаком косинуса наибольшего угла треугольника.

Следовательно, если числитель:

а) положителен, то треугольник остроугольный;

б) равен нулю, то треугольник прямоугольный;

с) отрицателен, то треугольник тупоугольный.

Задача 4. Даны действительные числа х и у. Если х и у отрицательны, то каждое значение заменить его модулем; если отрицательно только одно из них, то оба значения увеличить на 0,5; если оба значения неотрицательны и ни одно из них не принадлежит отрезку [0,5; 2], то оба значения уменьшить в 10 раз; во всех остальных случаях х и у оставить без изменения.

Задача 5. Заданы координаты точки х и у. Определить ее расположение в декартовой прямоугольной системе координат.

Здесь необходимо рассмотреть семь возможных вариантов: точка совпадает с началом координат, принадлежит одной из координатных осей, принадлежит одной из координатных четвертей. В случае принадлежности точки одной из координатных четвертей необходимо вывести на экран номер четверти; в случае принадлежности точки одной из осей необходимо вывести на экран название координатной оси (ось абсцисс или ось ординат).

2.3. Задания для контрольной работы

Составить алгоритм для расчета значений выражений. Реализовать алгоритм в Turbo Pascal. Отсутствующие в языке функции выразить через имеющиеся.

Вариант 1.

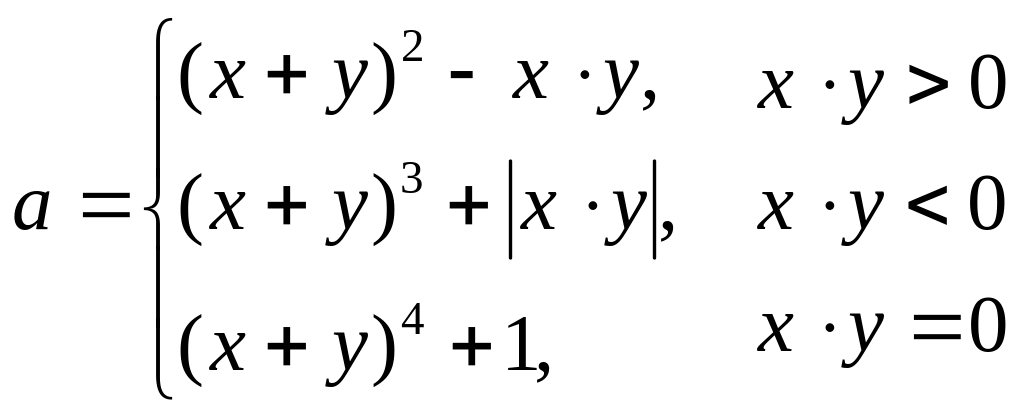
Вариант 2.

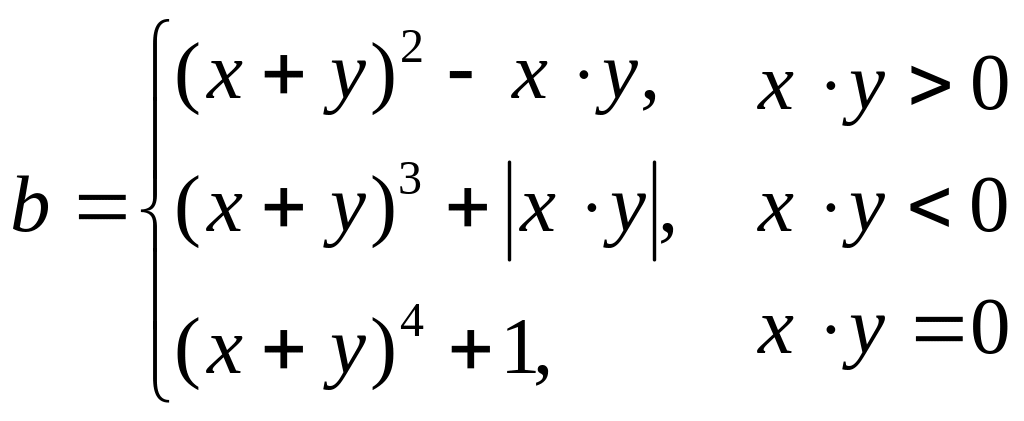
Вариант 3.

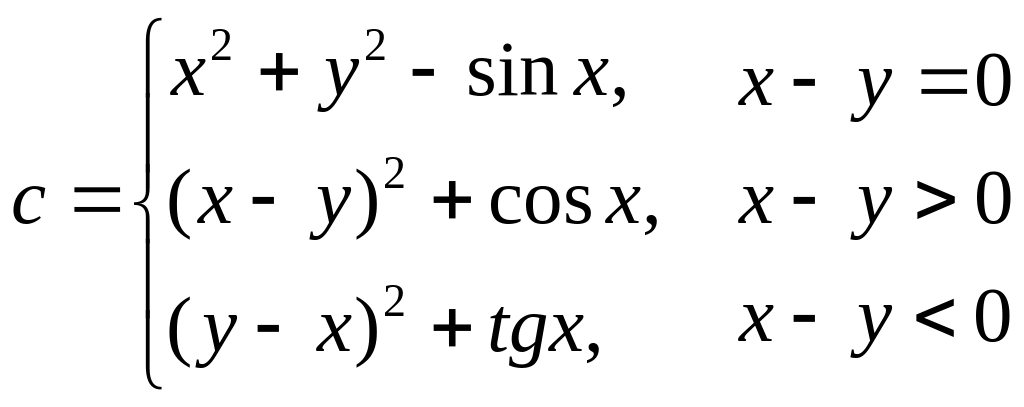
Вариант 4.

Вариант 5.

Вариант 6.

Вариант 7.

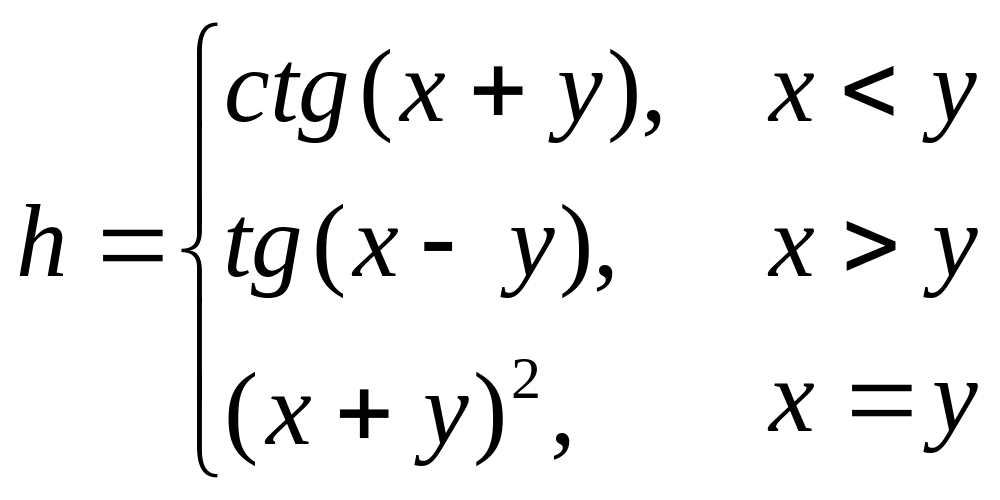
Вариант 8.

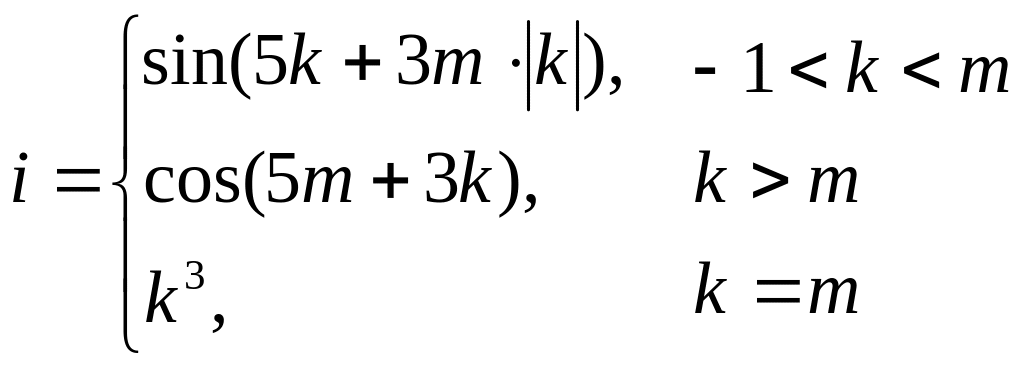
Вариант 9.

Вариант 10.

 Вариант 11.

 Вариант 12.

 Вариант 13.

 Вариант 14.

 Вариант 15.

 Вариант 16.

 Вариант 17.

 Вариант 18.

 Вариант 19.

 Вариант 20.

3. Алгоритмы с циклами

3.1. Примеры решения заданий

Задача 1. Дано натуральное число n. Вычислить n!.

Решение:

n! - это произведение всех натуральных чисел от 1 до п включительно. 0!=1!=1; 2!=12= 2; 3!= 23= 6; 4!=64=24 и т.д. Вообще, n!=(n-l)!n. Факториалы растут очень быстро. Существует формула Стирлинга для приближённого вычисления этой величины, полезная при изучении теории вероятностей, рядов. Её относительная погрешность стремится к нулю с ростом n:

Алгоритм решения задачи запишется в виде, представленном на рис. 3.1.

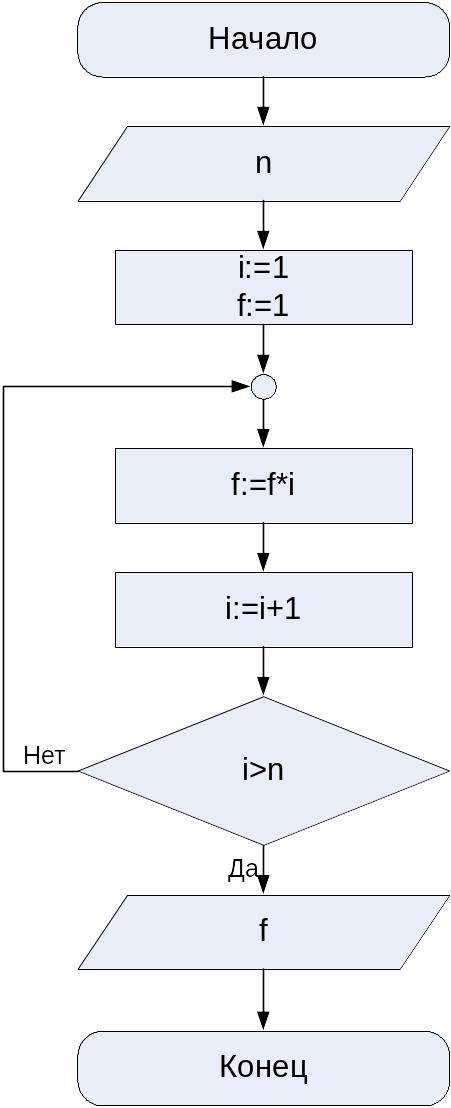
Рис. 3.7. Блок схема алгоритма решения задачи 1

Программа в Turbo Pascal будет иметь следующий вид:

Program factorial;

Var n,i,f: Integer;

Begin

Write('Введите натуральное число ');

ReadLn(n);

f:=1;

For i:=2 to n do f:=f*i;

WriteLn(n:40, ' f = ', f:0:0);

Write('По приближенной формуле_ Стирлинга:');

Write(n:5,'f =', Sqrt(2*Pi*n)*_ Exp(n*(Ln(n)-1)):5:3);

ReadLn;

End.

Задача 2. Дано натуральное число n. Вычислить:

a) б)

Решение:

а) Алгоритм решения задачи запишется в виде, представленном на рис. 3.2.

Программа в Turbo Pascal будет иметь следующий вид:

Program Square_a;

Var x: Extended;

i,n: Byte;

Begin

Write('Введите количество корней N = ');

ReadLn(n);

x:=0;

For i:=l to n do x:=Sqrt(2+x);

WriteLn(x);

ReadLn;

End.



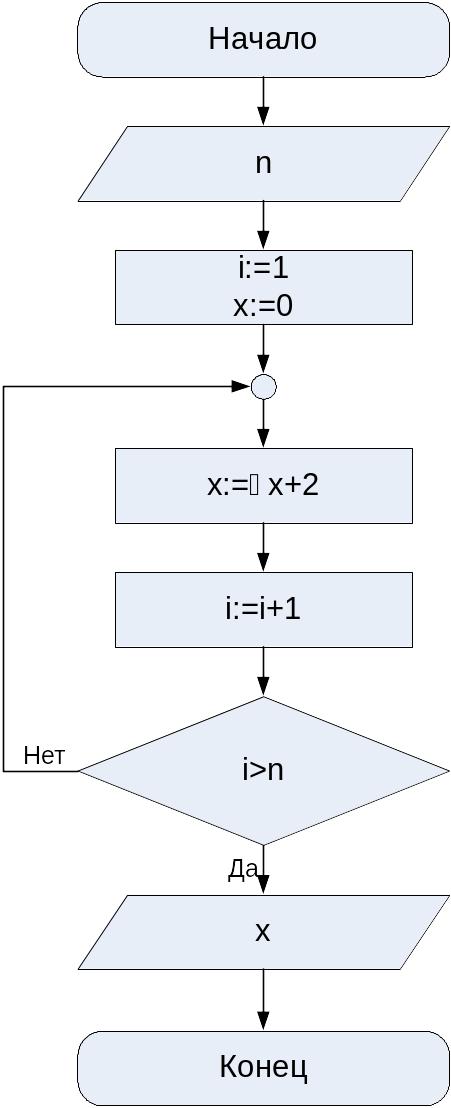
Рис. 3.8. Блок-схема алгоритма решения задачи 2

б) Алгоритм решения задачи будет иметь практически тот же вид, что и алгоритм для решения задачи а). Отличия заключаются лишь в организации цикла для расчета подкоренного выражения:

х:=0;

For i:=n downto 1 do x:=Sqrt(3*i+x);

Задача 3. Написать программу печати таблицы значений функции sin для аргумента, изменяющегося в заданных пределах с заданным шагом.

Решение

Исходными данными являются начальное значение аргумента Х_n, конечное значение аргумента X_k и шаг изменения аргумента dX. Все величины - вещественные и могут принимать любые значения на числовой оси. Результатом работы программы должна быть таблица, состоящая из двух столбцов - значений аргумента и соответствующих им значений функции. Вид таблицы приведен на следующем рис.:

X	Y
-4.00	0.76
-3.00	-0.14
-2.00	-0.91
-1.00	-0.84
0.00	0.00
1.00	0.84
2.00	0.91
3.00	0.14
4.00	-0.76

Алгоритм решения задачи запишется виде, представленном на рис. 3.3.

Программа в Turbo Pascal будет иметь следующий вид:

Program tab_fun;

Var x,y,Xn,Xk,dx:real;

Begin

Writeln('Введите значения Xn, Xk, dX');

Readln(Xn, Xk, dX);

Writeln(' ------------------------- ');

Writeln('| X | Y |');

Writeln(' ------------------------- ');

x:=Xn;

While x <= Xk do begin

у:=sin(x);

Writeln('|', х:9:2,' |', у:9:2,' |');

х:=х+dX;

End;

Writeln(' ------------------------- ');

End.

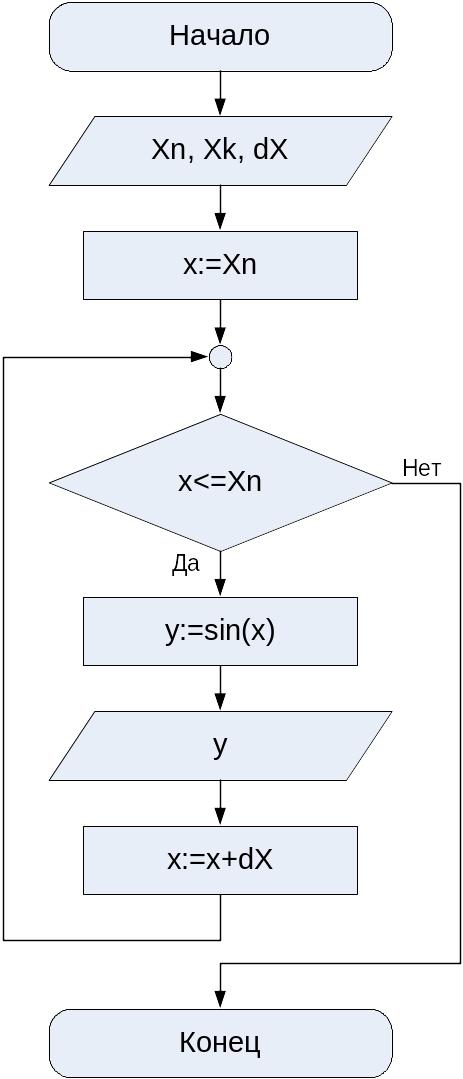
Рис. 3.9. Блок-схема решения задачи 3

Задача 4. Написать программу вычисления значения функции sin с помощью степенного ряда с точностью  по формуле:

Решение

Этот ряд сходится на всей числовой оси. Для достижения заданной точности требуется суммировать члены ряда до тех пор, пока абсолютная величина очередного члена не станет меньше или равна .

Запишем в общем виде формулу для вычисления n-го члена ряда:

Легко заметить, что (n+1)-й член ряда вычисляется после n-го, поэтому программа получится более простой и эффективной, если находить член ряда не «с нуля», а умножением предыдущего члена на некоторую величину.

Найдем эту величину. Для этого сначала запишем формулу для (n+1)-го члена ряда, подставив в предыдущее выражение (n+1) вместо n:

Теперь найдем выражение, на которое надо будет умножить С_n, чтобы получить С_n+1:

Определить заранее, сколько членов ряда потребуется просуммировать для достижения точности, невозможно, поскольку при анализе условия выхода используется переменная, вычисляемая на каждой итерации цикла. Такие циклы потенциально опасны, поэтому для предотвращения зацикливания полезно предусмотреть аварийный выход из цикла по достижении некоторого максимально допустимого количества итераций с печатью предупреждающего сообщения.

Программа в Turbo Pascal будет иметь следующий вид:

Program sinus;

{ макс-но допустимое кол-во итераций }

Const Maxlter = 500;

{ аргумент и точность }

Var x, eps: double;

{ член ряда и его сумма }

с, у: double;

n: integer; { номер члена ряда }

{ признак достижения точности }

done: boolean;

Begin

Writeln('Введите аргумент и точность;');

Readln(x, eps);

done:=true;

с:=x; { первый член ряда }

у:=с; { начальное значение суммы }

n := 1;

While abs(c) > eps do begin

{ очередной член ряда }

с:=-с*sqr(x)/2/n/(2*n+l);

{ добавление члена ряда к сумме}

у:=у+с;

inc(n); { переход к след. члену ряда}

If n <= Maxlter then Continue;

Writeln('Ряд расходится!');

{аварийный выход из цикла}

done := false;

Break;

End;

If done then Writeln('ApryмeнT: ',_ x:10:6, #13#10, 'Значение функции: ',_ у:10:6, #13#10, 'Вычислено с точностью ',_ eps:8:6, ' за ', n, ' итераций');

Readln;

End.

Максимально допустимое количество итераций удобно задать с помощью именованной константы. Для аварийного выхода из цикла применяется процедура break, которая обеспечивает переход к первому после цикла оператору. Символы #13#10 при выводе вызывают переход на следующую строку.

Поскольку выход в случае как аварийного, так и нормального завершения цикла происходит в одну и ту же точку программы, вводится булева переменная done, которая предотвращает печать значения функции после выхода из цикла, когда точность вычислений не достигнута. Создание подобных переменных-«флагов», принимающих значение «истина» в случае успешного окончания вычислений и «ложь» в противном случае, является распространенным приемом программирования.